Метод динамического программирования как алгоритмическое выражение достаточно общей теории управления

В изложении существа метода динамического программирования мы опираемся на книгу “Курс теории автоматического управления” (автор Палю де Ла Барьер: французское издание 1966 г., русское издание — “Машиностроение”, 1973 г.), хотя и не повторяем его изложения. Отдельные положения взяты из курса “Исследование операций” Ю.П.Зайченко (Киев, “Вища школа”, 1979 г.).

Метод динамического программирования работоспособен, если формальная интерпретация реальной задачи позволяет выполнить следующие условия:

1. Рассматриваемая задача может быть представлена как N‑шаговый процесс, описываемый соотношением:

X_{n + 1} = f(X_n, U_n, n), где n — номер одного из множества возможных состояний системы, в которое она переходит по завершенииn-ного шага; X_n — вектор состояния системы, принадлежащий упомянутому n-ному множеству; U_n — управление, выработанное на шаге n (шаговое управление), переводящее систему из возможного её состояния вn-ном множестве в одно из состояний (n + 1)‑го множества. Чтобы это представить наглядно, следует обратиться к рис. 4, о котором речь пойдет далее.

2. Структура задачи не должна изменяться при изменении расчетного количества шагов N.

3. Размерность пространства параметров, которыми описывается состояние системы, не должна изменяться в зависимости от количества шагов N.

4. Выбор управления на любом из шагов не должен отрицать выбора управления на предыдущих шагах. Иными словами, оптимальный выбор управления в любом из возможных состояний должен определяться параметрами рассматриваемого состояния, а не параметрами процесса, в ходе которого система пришла в рассматриваемое состояние.

Чисто формально, если одному состоянию соответствуют разные предыстории его возникновения, влияющие на последующий выбор оптимального управления, то метод позволяет включить описания предысторий в вектор состояния, что ведёт к увеличению размерности вектора состояния системы. После этой операции то, что до неё описывалось как одно состояние, становится множеством состояний, отличающихся одно от других компонентами вектора состояния, описывающими предысторию процесса.

5. Критерий оптимального выбора последовательности шаговых управлений U_n и соответствующей траектории в пространстве формальных параметров имеет вид:

V = V₀(X₀, U₀) + V₁(X₁, U₁) + …+ V_{N - 1}(X_{N- 1}, U_{N - 1}) + V_N(X_N) .

Критерий V принято называть полным выигрышем, а входящие в него слагаемые — шаговыми выигрышами. В задаче требуется найти последовательность шаговых управлений U_n и траекторию, которым соответствует максимальный из возможных полных выигрышей. По своему существу полный “выигрыш” V — мера качества управления процессом в целом. Шаговые выигрыши, хотя и входят в меру качества управления процессом в целом, но в общем случае не являются мерами качества управления на соответствующих им шагах, поскольку метод предназначен для оптимизации управления процессом в целом, а эффектные шаговые управления с большим шаговым выигрышем, но лежащие вне оптимальной траектории, интереса не представляют. Структура метода не запрещает при необходимости на каждом шаге употреблять критерий определения шагового выигрыша V_n, отличный от критериев, принятых на других шагах.

С индексом n — указателем-определителем множеств возможных векторов состояния — в реальных задачах может быть связан некий изменяющийся параметр, например: время, пройденный путь, уровень мощности, мера расходования некоего ресурса и т.п. То есть метод применим не только для оптимизации управления процессами, длящимися во времени, но и к задачам оптимизации многовариантного одномоментного или нечувствительного ко времени решения, если такого рода “безвременные”, “непро­цес­сные” задачи допускают их многошаговую интерпретацию.

Теперь обратимся к рис. 4 — рис. 6, повторяющим взаимно связанные рис. 40, 41, 42 из курса теории автоматического управления П. де Ла Барьера.

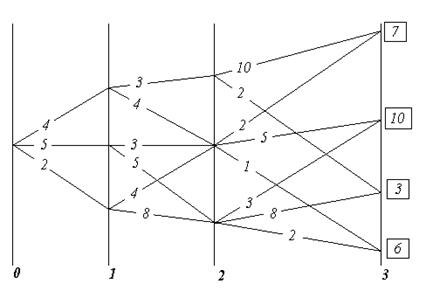Рис. 4. К существу метода динамического программирования. Матрица возможностей.

На рис. 4 показаны начальное состояние системы — «0» и множества её возможных последующих состояний — «1», «2», «3», а также возможные переходы из каждого возможного состояния в другие возможные состояния. Всё это вместе похоже на карту настольной детской игры, по которой перемещаются фишки: каждому переходу-шагу соответствует свой шаговый выигрыш, а в завершающем процесс третьем множестве — каждому из состояний системы придана его оценка, помещенная в прямоугольнике. Принципиальное отличие от игры в том, что гадание о выборе пути, употребляемое в детской игре, на основе бросания костей или вращения волчка и т.п., в реальном управлении недопустимо, поскольку это — передача целесообразного управления тем силам, которые способны управлять выпадением костей, вращением волчка и т.п., т.е. тем, для кого избранный в игре «генератор случайностей» — достаточно (по отношению к их целям) управляемое устройство.

Если выбирать оптимальное управление на первом шаге, то необходимо предвидеть все его последствия на последующих шагах. Поэтому описание алгоритма метода динамического программирования часто начинают с описания выбора управления на последнем шаге, ведущем в одно из завершающих процесс состояний. При этом ссылаются на «педагогическую практику», которая свидетельствует, что аргументация при описании алгоритма от завершающего состояния к начальному состоянию легче воспринимается, поскольку опирается на как бы уже сложившиеся к началу рассматриваемого шага условия, в то время как возможные завершения процесса также определены.

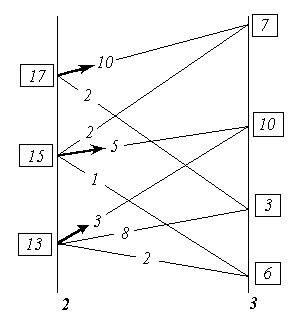Рис. 5. К существу метода динамического программирования. Анализ переходов.

В соответствии с этим на рис. 5 анализируются возможные переходы в завершающее мно­жество состояний «3» из каждого возможного состояния в ему предшествую­щем множестве состояний «2», будто бы весь предшествующий путь уже пройден и осталось последним выбором опти­мального ша­гового управления завершить весь процесс. При этом для каждого из состояний во множестве «2» определяются все полные выигрыши как сумма = «оценка перехода» + «оценка завершающего состояния». Во множестве «2» из полученных для каждого из состояний, в нём возможных полных выигрышей, определяется и запоминается максимальный полный выигрыш и соответствующий ему переход (фрагмент траектории). Максимальный полный выигрыш для каждого из состояний во множестве «2» взят в прямоугольную рамку, а соответствующий ему переход отмечен стрелкой. Таких оптимальных переходов из одного состояния в другие, которым соответствует одно и то же значение полного выигрыша, в принципе может оказаться и несколько. В этом случае все они в ме­тоде неразличимы и эквивалентны один другому в смысле по­строенного критерия оптимально­сти вы­бора траектории в про­стра­нстве параметров, которы­ми опи­сыва­ет­ся система.

После этого мно­жество «2», предшествовав­шее завер­шаю­ще­му процесс множеству «3», мож­но рассматривать в качестве завер­шаю­щего, посколь­ку из­вестны оценки каждого из его возможных состояний (мак­­си­маль­ные полные выигрыши) и дальнейшая оптимизация последовательности шаговых упра­влений и выбор оптимальной траектории могут быть проведены только на ещё не рас­смотренных множествах, предшествующих множеству «2» в оптимизируемом процессе (т.е. на множествах «0» и «1»).

Таким образом, процедура, иллюстрируемая рис. 5, работоспособна на каждом алгоритмическом шаге метода при переходах из n-го в (n - 1)-е множество, начиная с завершающего N‑ного множества до начального состояния системы.

В результате последовательного попарного перебора множеств, при прохождении всего их набора, определяется оптимальная последовательность преемственных шаговых управлений, максимально возможный полный выигрыш и соответствующая им траектория. На рис. 6 утолщённой линией показана оптимальная траектория для рассматривавшегося примера.

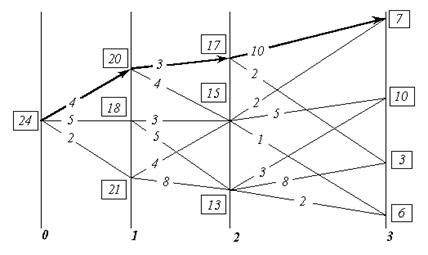Рис. 6. К существу метода динамического программирования. Оптимальная траектория.

В рассмотренном примере критерий оптимальности — сумма шаговых выигрышей. Но критерий оптимальности может быть построен и как произведение обязательно неотрицательных сомножителей.

Поскольку результат (сумма или произведение) не изменяется при изменении порядка операций со слагаемыми или сомножителями, то алгоритм работоспособен и при переборе множеств возможных состояний в порядке, обратном рассмотренному: т.е. от исходного к завершающему множеству возможных состояний.

Если множества возможных состояний упорядочены в хронологической последовательности, то это означает, что расчетная схема может быть построена как из реального настоящего в прогнозируемое определённое будущее, так и из прогнозируемого определённого будущего в реальное настоящее. Это обстоятельство говорит о двух неформальных соотношениях реальной жизни, лежащих вне алгоритма:

1. Метод динамического программирования формально алгорит­мически нечувствителен к характеру причинно-следст­вен­ных обусловленностей (в частности, он не различает причин и следствий). По этой причине каждая конкретная интерпретация метода в прикладных задачах должна строиться с неформальным учетом реальных обусловленностей следствий причинами.

2. Если прогностика в согласии с иерархически высшим объемлющим управлением, а частное вложенное в объемлющее управление осуществляется квалифицировано, в силу чего процесс частного управления протекает в ладу с иерархически высшим объемлющим управлением, то НЕ СУЩЕСТВУЕТ УПРАВЛЕНЧЕСКИ ЗНАЧИМОЙ РАЗНИЦЫ МЕЖДУ РЕАЛЬНЫМ НАСТОЯЩИМ И ИЗБРАННЫМ БУДУЩИМ.

Процесс целостен, по какой причине ещё не свершившееся, но уже нравственно избранное и объективно не запрещённое Свыше будущее, в свершившемся настоящем защищает тех, кто его творит на всех уровнях: начиная от защиты психики от наваждений до защиты от целенаправленной “физи­чес­кой” агрессии. То есть, если матрица возможных состояний (она же матрица возможных переходов) избрана в ладу с иерархически высшим объемлющим управлением, то она сама — защита и оружие, средство управления, на которое замкнуты все шесть приоритетов средств обобщённого оружия и управления.

Объективное существование матриц возможных состояний и переходов проявляется в том, что в слепоте можно “забрести” в некие матрицы перехода и прочувствовать на себе их объективные свойства. Последнее оценивается субъективно, в зависимости от отношения к этим свойствам, как полоса редкостного везения либо как нудное “возвращение на круги своя” или полоса жестокого невезения.

Но для пользования методом динамического программирования и сопутствующими его освоению неформализованными в алгоритме жизненными проявлениями матриц перехода, необходимо СОБЛЮДЕНИЕ ГЛАВНОГО из условий:

В задачах оптимизации процессов управления метод динамического программирования <реального будущего: — по умолчанию> работоспособен только, если определён вектор целей управления, т.е. должно быть избрано завершающее процесс определённое состояние.

В реальности это завершающее определённое состояние должно быть заведомо устойчивым и приемлемым процессом, объемлющим и несущим оптимизируемый методом частный процесс. Но выбор и определение определённых характеристик процесса, в который должна войти управляемая система по завершении алгоритма метода лежит вне этого метода — в области “мистики” или в области методов, развитых в нематематических по своему существу науках и ремёслах.

«Каково бы ни было состояние системы перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным», — Е.С.Вентцель, “Исследование операций. Задачи, принципы, методология.” (М., “Наука”, 1988 г., стр. 109).

Неспособность определить вектор целей управления (достиже­ни­ем которого должен завершиться оптимизируемый в методе процесс) и (или) неспособность выявить исходное состояние объекта управления не позволяет последовать этой рекомендации, что объективно закрывает возможности к использованию метода динамического программирования, поскольку начало и конец процесса должны быть определены в пространстве параметров, на которых построена математическая (или иная) модель метода, которая должна быть метрологически состоятельной, что является основой её соотнесения с реальностью. Причём определённость завершения оптимизируемого процесса имеет управленчески боль­шее значение, чем ошибки и некоторые неопределённости в идентификации (выявлении) начального состояния объекта управления.

Это тем более справедливо для последовательных многовариантных шаговых переходов, если матрица возможных состояний вписывается в пословицу «Все дороги ведут в “Рим”», а которые не ведут в “Рим”, — ведут в небытие. Для такого рода процессов, если избрана устойчивая во времени цель и к ней ведут множество траекторий, то при устойчивом пошаговом управлении “расстояние” между оптимальными траекториями, идущими к одной и той же цели из различных исходных состояний, от шага к шагу сокращается, вплоть до полного совпадения оптимальных траекторий, начиная с некоторого шага. Это утверждение тем более справедливо, чем более определённо положение завершающего процесс вектора целей в пространстве параметров. По аналогии с математикой это можно назвать асимптотическим множеством траекторий: асимптотичность множества траекторий выражается в том, что «все дороги ведут в “Рим”…»

И в более общем случае, рекомендации Нового Завета и Корана утверждают возможность обретения благодати, милости Вседержителя вне зависимости от начального состояния (греховности человека) в тот момент, когда он очнулся и увидел свои дела такими, каковы они есть.

Другое замечание относится уже к практике — к вхождению в матрицу перехода. Если начальное состояние системы определено с погрешностью, большей чем допустимая для вхождения в матрицу перехода из реального начального состояния в избранное конечное, то управление на основе самого по себе безошибочного алгоритма метода динамического программирования приведет к совсем иным результатам, а не расчетному оптимальному состоянию системы. Грубо говоря, не следует принимать за выход из помещения на высоком этаже открытое в нём окно.

То есть методдинамического программирования, необходимостью как определённости в выборе конечного состояния-процесса, так и выявления истинного начального состояния, сам собой защищён от применения его для наукообразной имитации оптимизации управления при отсутствии такового. Это отличает метод динамического программирования, в частности от аппарата линейного программирования[69], в который можно сгрузить экспромтные оценки “экспертами” весовых коэффициентов в критериях оптимизации Min (Z) либо Max (Z).

* * *

Эта сама собой защищённость от недобросовестного использования косвенно отражена и в литературе современной экономической науки: поскольку она не определилась с тем, что является вектором целей управления по отношению к экономике государства, то не встречаются и публикации об использовании аппарата динамического программирования для оптимизации управления макроэкономическими системами регионов и государств в целом на исторически длительных интервалах времени.

Примерами тому “Математическая экономика на персональном компьютере” под ред. М.Кубонива[70], в которой глава об управлении в экономике содержит исключительно макроэкономические интерпретации аппарата линейного программирования (прямо так и названа “Управление в экономике. Линейное программирование и его применение”), но ничего не говорит о векторе целей управления и средствах управления; в ранее цитированном учебнике Ю.П.Зай­че­н­ко описание метода динамического программирования также построено на задачах иного характера.

Однако при мотивации отказа от макроэкономических интерпретаций метода динамического программирования авторы обычно ссылаются на так называемое в вычислительной математике «про­кля­тие размерности», которое выражается в том, что рост размерности пространства параметров задачи N вызывает рост объема вычислений, пропорциональный N ^k, где показатель степени k > 1 . Такой нелинейный сверхпропорциональный рост объема вычислений действительно делает многие вычислительные работоспособные процедуры никчемными в решении практических задач как из-за больших затрат машинного времени компьютеров, так и из-за накопления ошибок в приближённых вычислениях. Но это «проклятие размерности» относится не только к методу динамического программирования, но и к другим методам, которые, однако, встречаются и в их макроэкономических интерпретациях.

* *
*

ВАЖНО ОБРАТИТЬ ВНИМАНИЕ И ПОНЯТЬ: Если в математике видеть науку об объективной общевселенской мере (через “ять”), а в её понятийном, терминологическом аппарате и символике видеть одно из предоставленных людям средств описания объективных частных процессов, выделяемых ими из некоторых объемлющих процессов, то всякое описание метода динамического программирования есть краткое изложение всей ранее изложенной достаточно общей теории управления, включая и её мистико-религи­оз­ные аспекты; но — на языке математики.

Чтобы пояснить это, обратимся к рис. 7, памятуя о сделанном ранее замечании об определённости начального состояния с достаточной для вхождения в матрицы перехода точностью.

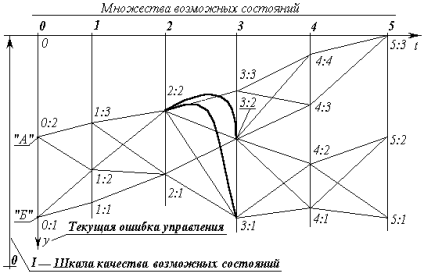Рис. 7. Динамическое программирование, Различение и достаточно общая теория управления

На нём показаны два объекта управления «А» и «Б» в начальном состоянии; три объективно возможных завершающих состояния (множество «5»); множества («1» — «4») промежуточных возможных состояний; и пути объективно возможных переходов из каждого состояния в иные.

Рис. 7 можно уподобить некоторому фрагменту общевселенской меры развития (многовариантного предопределения бытия) — одной из составляющих в триединстве «материя-информация-мера».

Если принять такое уподобление рис. 7, то объективно возможен переход из любого начального состояния «0:1» или «0:2» в любое из завершающих состояний «5:1», «5:2», «5:3». Но эта объективная возможность может быть ограничена субъективными качествами управленцев, намеревающихся перевести объекты «А» и «Б» из начального состояния в одно из завершающих состояний.

Если дано Свыше Различение, то управленец «А» (или «Б») снимет с объективной меры “кальку”, на которой будет виден хотя бы один из множества возможных путей перевода объекта из начального состояния во множество завершающих. Если Различение не дано, утрачено или отвергнуто в погоне за вожделениями, или бездумной верой в какую-либо традицию, но не Богу по совести, то на “кальке” будут отсутствовать какие-то пути и состояния, но могут “появиться” объективно невозможные пути и состояния, объективно не существующие в истинной Богом данной мере — предопределении бытия. Кроме того, по субъективному произволу управленца выбирается и желанное определённое завершающее состояние из их множества. Соответственно следование отсебятине или ошибка в выборе предпочтительного завершающего состояния может завершиться катастрофой с необратимыми последствиями.

Но матрица возможных состояний, показанная на рис. 7, вероятностно предопределяет только частный процесс в некой взаимной вложенности процессов. По этой причине каждое из начальных состояний «0:1», «0:2» может принадлежать либо одному и тому же, либо различным объемлющим процессам, в управленческом смысле иерархически высшим по отношению к рассматриваемому; то же касается и каждого из завершающих состояний «5:1», «5:2», «5:3» в паре «исходное — завершающее» состояния. Каждый из объемлющих процессов обладает их собственными характеристиками и направленностью течения событий в нём.

Может оказаться, что цель «5:1» очень привлекательна, если смотреть на неё из множества начальных неудовлетворительных состояний. Но не исключено, что объемлющий процесс, к которому завершающее состояние «5:1» принадлежит, как промежуточное состояние, в силу взаимной вложенности процессов, на одном из последующих шагов завершается полной и необратимой катастрофой. Например, цель «5:1» — не опоздать на “Титаник”, выходящий в свой первый рейс, … ставший трагическим и последним. Чтобы не выбирать такую цель из множества объективно возможных, необходимо быть в ладу с иерархически наивысшим объемлющим управлением, которое удержит частное ладное с ним управление от выбора такой цели, принадлежащей к обречённому на исчезновение процессу.

Но если рис. 7 — “калька” с объективной меры, то может статься, что какое-то завершающее состояние, являющееся вектором целей — отсебятина, выражающая желание “сесть на два поезда сразу”. Иными словами, разные компоненты вектора целей принадлежат к двум или более взаимно исключающим друг друга иерархически высшим объемлющим процессам протекающим одновременно.

Это один из случаев неопределённости и дефективности вектора целей, делающий метод динамического программирования неработоспособным, а реальный процесс “управления” неустойчивым, поскольку одна и та же “лодка” не может пристать и к правому, и к левому берегу одновременно, даже если привлекательные красоты на обоих берегах реки, при взгляде издали — из-за поворота реки — совмещаются, создавая видимость подходящего для пикника весьма уютного места. Чтобы не выбрать такого вектора целей, также необходимо, чтобы Свыше было дано Различение правого и левого “бере­гов” потока бытия.

То есть алгоритму динамического программирования, даже если его можно запустить, сопутствует ещё одно внешнее обстоятельство, которое тоже очевидно, “само собой” разумеется, но в большинстве случаев игнорируется: завершающее частный оптимизируемый процесс состояние должно принадлежать объемлющему процессу, обладающему заведомо приемлемыми собственными характеристиками течения событий в нём.

После избрания цели, принадлежащей во взаимной вложенности к объемлющему процессу с приемлемыми характеристиками устойчивости и направленностью течения событий в нём, необходимо увидеть пути перехода и выбрать оптимальную последовательность преемственных шагов, ведущую в избранное заверша­ю­щее частный процесс состояние; т.е. необходимо избрать концеп­цию управления.

Концепция управления в объективной мере, обладает собственными характеристиками, которые совместно с субъективными характеристиками субъекта-управленца, порождают вероятностную предопределённость осуществления им концепции управления. Значение вероятностной предопределённости успешного завершения процесса — объективная иерархически высшая мера, оценка замкнутой системы «объект + управленец + концепция», в отличие от вероятности — объективной меры системы «объект + объективно существующая концепция управления».

Поэтому, чем ниже вероятность перевода объекта в желательное завершающее состояние, тем выше должна быть квалификация управленца, повышающая значение вероятностной предопределённости успешного завершения процесса управления.

Соответственно сказанному, для администратора признание им некой концепции управления может выражаться в его уходе с должности по собственной инициативе, проистекающей из осознания им своей неспособности к осуществлению признанной им концепции управления; а неприятие концепции может выражаться, как заявление о её принятии и последующие искренние ревностные, но неквалифицированные усилия по её осуществлению. Они приведут к тому, что концепция будет дискредитирована, поскольку квалифицированные управленцы, способные к её осуществлению, не будут допущены до управления по личной ревности, жажде славы, зарплаты или ещё чего-то со стороны благонамеренного самонадеянного неквалифицированного недочеловека.

Вследствие нетождественности вероятности (математи­чес­кой) и вероятностной предопределённости очень хорошая концепция может быть загублена плохими исполнителями её: на двухколесном велосипеде ездить лучше, чем на трехколёсном, но не все умеют; но некоторые ещё будут доказывать, что на двухколесном и ездить нельзя, поскольку он падает и сам по себе, а не то что с сидящим на нём человеком, тем более на ходу, — если они ранее не видели, как ездят на двухколесном; а третьи, не умея и не желая учиться ездить самим, из ревности не отдадут велосипед тем, кто умеет.

Поэтому после принятия концепции к исполнению необходимо придерживаться концептуальной самодисциплины самому и взращивать концептуальную самодисциплину в окружающем обществе. То есть необходимо поддерживать достаточно высокое качество управления на каждом шаге всеми средствами, чтобы не оказаться к началу следующего шага в положении, из которого в соответствии с избранной концепцией управления перевод объекта в избранное завершающее состояние невозможен. Этот случай — уклонение с избранного пути «2:2» ® «3:3» показан: дуга «2:2» ® «3:1» — необратимый срыв управления, после которого невозможен переход в состояние «5:3»; дуга «2:2» ® «3:2» — обратимый срыв управления, в том смысле что требуется корректирование концепции, исходя из состояния «3:2», рассматриваемого в качестве начального.

Если на рис. 7 объективной иерархически высшей мере качества состояний, в которых могут находиться объекты субъектов-управленцев «А» и «Б», соответствует шкала качества возможных состояний «I», то для их блага целесообразен переход из множества состояний «0» в состояние «5:3». Но выбор ими направленности шкалы оценки качества состояний нравственно обусловлен и субъективен: либо как показано на рис. 7 «I», либо в противоположном «I» направлении.

Если на рис. 7 возможные состояния сгруппированы во множества «1», «2», «3», «4», «5» по признаку синхронности, то в координатных осях 0ty, при шкале качества состояний «I» расстояние от оси 0t до любой из траекторий — текущая ошибка управления при движении по этой траектории. Площадь между осью 0t и траекторией — интеграл по времени от текущей ошибки. Он может быть использован как критерий-минимум оптимальности процесса управления в целом, т.е. в качестве полного выигрыша, являющегося в методе динамического программирования мерой качества, но не возможных состояний, не шагов-переходов из одного состояния в другое, а всей траектории перехода. Но в общем случае метода шаговые выигрыши могут быть построены и иначе.

Если принят критерий оптимальности типа минимум[71] значения интеграла по времени от текущей ошибки управления (на рис. 7 это — площадь между осью 0t и траекторией перехода), то для субъекта «А» оптимальная траектория — «0:2» ® «1:3» ® «2:2» ® «3:3» ® «4:4» ® «5:3»; а для субъекта «Б» оптимальная траектория — «0:1» ® «1:2» ® «2:2» ® «3:3» ® «4:4» ® «5:3».

Срывы управления «1:2» ® «2:1» ® «3:1»; «2:2» ® «3:1»; «2:2» ® «3:2» ® «4:1»; «3:2» ® «4:2» — полная необратимая катастрофа управления по концепции, объективно возможной, но не осуществлённой по причине низкого качества текущего управления в процессе перевода объекта в избранное конечное состояние «5:3». Все остальные срывы управления обратимы в том смысле, что требуют коррекции концепции и управления по мере их выявления.

То есть метод динамического программирования в схеме упра­вления «предиктор-корректор» работоспособен, а сама схема развертывается, как его практическая реализация.

Возможны интерпретации метода, когда в вектор контрольных параметров (он является подмножеством вектора состояния) не входят какие-то характеристики объекта, которые тем не менее, включены в критерий выбора оптимальной траектории. Например, если в состоянии «0:2» различные субъекты не различимы по их исходным энергоресурсам, а критерий выбора оптимальной траектории чувствителен к энергозатратам на переходах, то такому критерию может соответствовать в качестве оптимальной траектория «0:2» ® «1:2» ® «2:1» ® «3:2» ® «4:3» ® «5:3» или какая-то иная, но не траектория «0:2» ® «1:3» ® «2:2» ® «3:3» ® «4:4» ® «5:3», на которой достигается минимум интеграла от текущей ошибки управления.

Это означает, что управленец, в распоряжении которого достаточный энергопотенциал, может избрать траекторию «0:2» ® «1:3» ® «2:2» ® «3:3» ® «4:4» ® «5:3»; но если управленец с недостаточным для такого перехода энергопотенциалом не видит траектории «0:2» ® «1:2» ® «2:1» ® «3:2» ® «4:3» ® «5:3», для прохождения которой его энергопотенциал достаточен, то состояние «0:2» для него субъективно тупиковое, безвыходное, хотя объективно таковым не является. Это говорит о первенстве Различения, даваемого Свыше непосредственно каждому, перед всем прочими способностями, навыками и знаниями.

Кроме того, этот пример показывает, что на одной и той же “кальке” с матрицы возможных состояний, соотносимой с полнотой реальности, можно построить набор критериев оптимальности, каждый из частных критериев в котором употребляется в зависимости от конкретных обстоятельств осуществления управления. И каждой компоненте этого набора соответствует и своя оптимальная траектория. Компоненты этого набора критериев, так же как и компоненты в векторе целей, могут быть упорядочены по предпочтительности вариантов оптимальных траекторий. Но в отличие от вектора целей, когда при идеальном управлении реализуются все без исключения входящие в него цели, несмотря на иерархическую упорядоченность критериев оптимальности, один объект может переходить из состояния в состояние только по единственной траектории из всего множества оптимальных, в смысле каждого из критериев в наборе, траекторий. Критерии оптимальности выбора, входящие в иерархически организованный набор критериев, не обязательно могут быть удовлетворены все одновременно. Для управления необходимо, чтобы процесс отвечал хотя бы одному из множества допустимых критериев.

Может сложиться так, что один субъект реализует концепцию «0:2» ® «1:2» ® «2:1» ® «3:2» ® «4:3» ® «5:3», а другой «0:2» ® «1:3» ® «2:2» ® «3:3» ® «4:4» ® «5:3» в отношении одного и того же объекта. Хотя конечные цели совпадают, но тем не менее, если управленцы принадлежат к множеству управленцев одного и того же уровня в иерархии взаимной вложенности процессов, то это — конкуренция, “спортивная” гонка или концептуальная война; если они принадлежат к разным иерархическим уровням в одной и той же системе, то это — антагонизм между её иерархическими уровнями, ведущий как минимум к падению качества управления в смысле, принятом на её иерархически наивысшем уровне, а как максимум — к распаду системы. Арбитр — иерархически высшее по отношению к ним обоим объемлющее управление. Тем более, если завершающие цели различны, то это — концептуальная война, обостряющаяся по ходу процесса.

Из сказанного следует, что алгоритм динамического программирования и рис. 7, иллюстрирующий некоторые аспекты его приложений, является довольно прозрачным намеком на весьма серьёзные жизненные обстоятельства. В целом же метод динамического программирования в его абстрактной постановке (т.е. не привязанной к какой-либо практической задаче) позволяет сформировать систему образно-логических представлений о процессах управления вообще, и вписывать в эту схему все практические жизненные управленческие потребности как одной личности, так и общества. Это необходимо для осознанного вхождения в управление даже в том случае, если управление реально строится на основе каких-то других моделей.