Простые волновые обмотки

Характерные признаки простых волновых обмоток:

1. ;

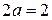2. ;

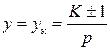3. не требуется применение уравнителей I рода.

Принцип выполнения простой волновой обмотки рассмотрим на примере ЭМПТ, 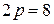(рис. 1.22).

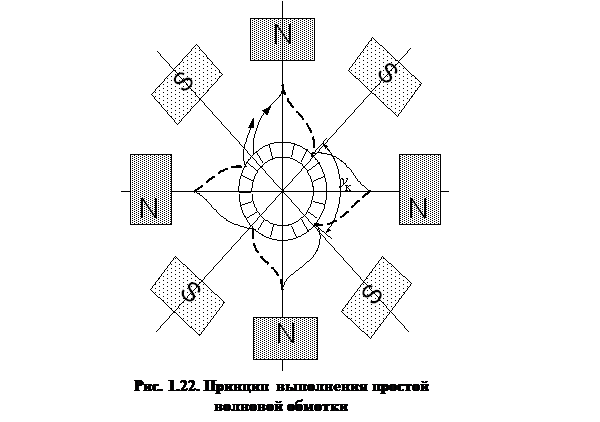
При одном обходе якоря (рис. 1.22) сделано р – шагов по коллектору (в данном случае – 4 шага), и оказались пройденными все коллекторные пластины, кроме одной (справа или слева от начальной), тогда

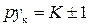(1.56)

Тогда шаг обмотки, равный шагу по коллектору:

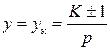– целое число, (1.57)

при этом знак «–» соответствует неперекрещивающейся обмотке;

«+» – перекрещивающейся обмотке.

Простая волновая обмотка называется последовательной, т.к. она независимо от числа пар полюсов образует 2 параллельные ветви (рис. 1.23):

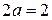(1.58)

Необходимое число щёток простой волновой обмотки:

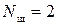(1.59)

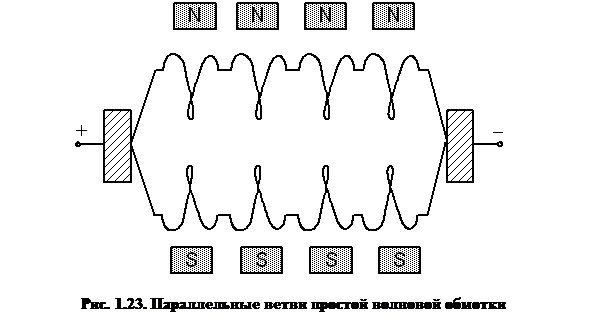
Поскольку каждая из ветвей простой волновой обмотки проходит под всеми полюсами, то неравенство потоков полюсов (магнитная несимметрия, вызванная различными факторами) не вызывает неравенства ЭДС, и не появляются уравнительные токи, и поэтому не требуется применение уравнителей I рода.

1.5.5. Развёрнутая схема простой волновой обмотки (пример)

Выполним развёрнутую схему простой волновой обмотки со следующими данными:

;

.

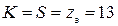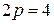Рассчитаем шаги обмотки:

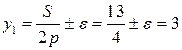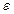, где – число, дополняющее отношение 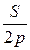до целого числа;

.

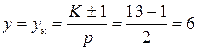
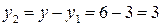Предварительно выполним схему соединений секционных сторон, по шагам (рис. 1.24).

По данной схеме выполним развёрнутую схему простой петлевой обмотки, которая представлена на рис. 1.25.

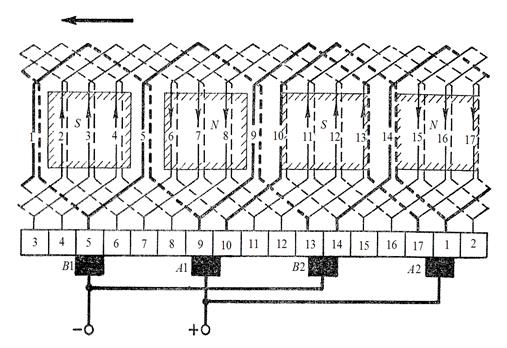
Рис. 1.25. Развернутая схема простой волновой обмотки

На рис. 1.25 выделены две начальные секции.

Установлено полное число щёток:

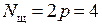. (1.60)

Данная обмотка имеет 2 параллельные ветви, каждая состоит из 5 секций.