Интегрирующее (идеальное) звено.
Уравнение и передаточная функция звена:
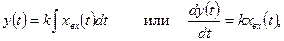
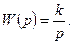
В случае интегрирующего звена параметр k является коэффициентом передачи звена по скорости, численно равным скорости изменения выходной величины при единичном значении входной величины.
Если входная и выходная величины имеют одинаковую размерность, то коэффициент k измеряется в [с-1]. В этом случае его принято обозначать через 1/Т, а Т называть постоянной времени интегрирующего звена.
Частотные и временные функции звена:
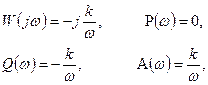
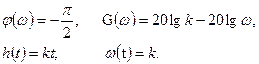
В качестве примера элемента, характеристики которого приближенно соответствуют характеристикам идеального интегрирующего звена, можно назвать двигатель постоянного тока с независимым возбуждением и малой электромеханической инерцией. Входной величиной для него является напряжение на зажимах якоря, а выходной - угол поворота вала.
Дифференцирующее (идеальное) звено.
Уравнение и передаточная функции звена:
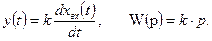
Выходная величина пропорциональна скорости изменения входной величины.
Если входная и выходная величины имеют одинаковую размерность, то коэффициент k измеряется в секундах. В этом случае его принято обозначать через Т и называть постоянной времени дифференцирующего звена.
Выражение для основных функций:
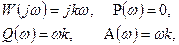
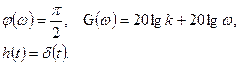
Апериодическое (первого порядка) звено.
Описывается дифференциальным уравнением
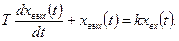
Передаточные и частотные передаточные функции:
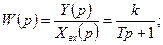
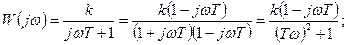
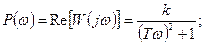
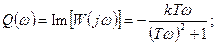
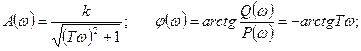
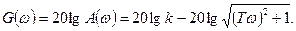
В таблицах 2 и 3 приводятся временная и частотная характеристики типовых звеньев.
Таблица 2
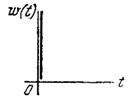
| Тип звена и его передаточная функция | Переходная функция h(t) | Функция веса w(t) |
| Безынерционное W(p) = k |
 h(t) = k×1(t)
h(t) = k×1(t)
|
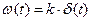
|
Апериодическое 1-го порядка
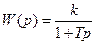
|
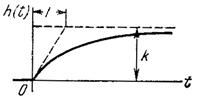
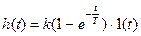
|
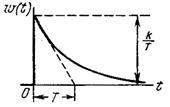
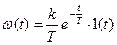
|
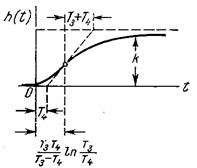
Апериодическое 2-го порядка
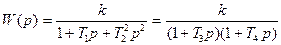 , ,
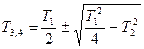
 (T1 > 2T2; T3 > T4) (T1 > 2T2; T3 > T4)
| 
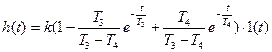
| 
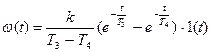
|
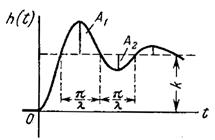
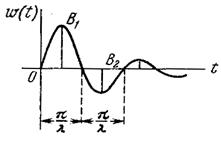
Колебательное
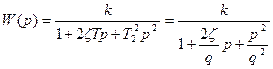 , ,
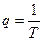
| 
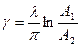 ,
g = zp, ,
g = zp, 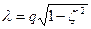 , ,
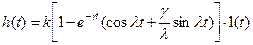
| 
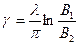 , , 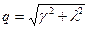 , ,
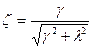 , , 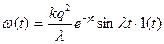
|
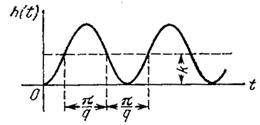
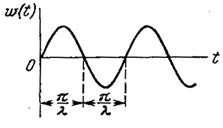
Консервативное
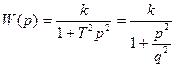 , , 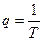
| 
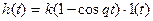
| 
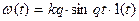
|
Таблица 3
| Тип звена и частотная передаточная функция | Амплитудно-фазовая | Амплитудная и фазовая | Логарифмические |
| Безынерционное W(jω) = k |
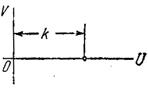
| 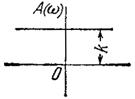 A(ω) = k, ψ = 0
A(ω) = k, ψ = 0
|
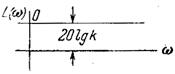
|
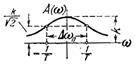
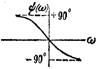
Апериодическое 1-го порядка
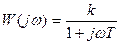
|
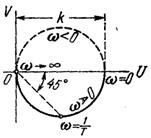
|  
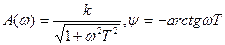
|
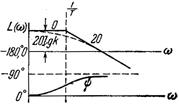
|
Апериодическое 2-го порядка
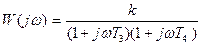
|
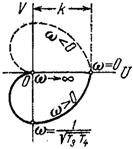
| 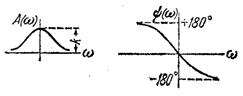
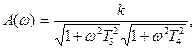
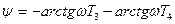
|
|
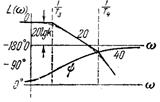
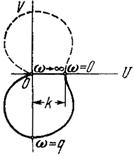
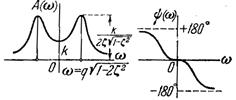
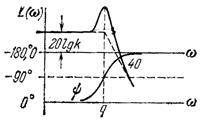
Колебательное
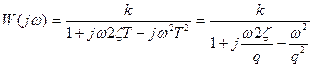
|
| 
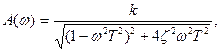
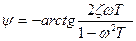
|
|
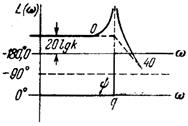
Консервативное
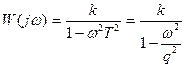
|
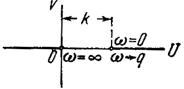
| 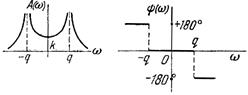 A(w)=
A(w)= 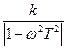 ,
j=0 при –q<w<q,
j=-180 при w>q,
j=180 при w<-q, ,
j=0 при –q<w<q,
j=-180 при w>q,
j=180 при w<-q,
|
|
Рассмотрим пример 1.
Объектом анализа является RLС схема, изображенная на рисунке 1.
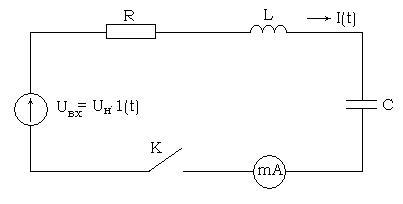
Рисунок 1 – RLС-цепь как объект анализа переходного процесса
На основании второго закона Кирхгофа для RLС схемы можем записать уравнение
Uвх(t) = UR (t) + UL(t) + UC, (t) (1)
или
Uвх(t) = I(t)R + L 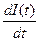 +
+ 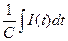 , (2)
, (2)
Введем новую переменную q(t) — электрический заряд, тогда
I(t) = 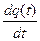 ; (3)
; (3)
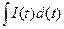 =q(t); (4)
=q(t); (4)
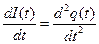 ; (5)
; (5)
подставим (3), (4), (5) в (2), получим:
Uвх(t) = R 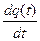 + L
+ L 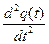 +
+ 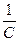 q(t) (6)
q(t) (6)
или
R 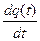 + L
+ L 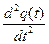 +
+ 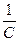 q(t) = Uвх(t) (7)
q(t) = Uвх(t) (7)
Введем обозначения:
q(t) = y(t), UВХ = f(t), a0 = R, a1 = L, a2 = 1/C, b0 = 1
Перепишем уравнение (7) с учетом новых обозначений в виде:
a0 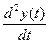 + a1
+ a1 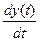 + a2×y(t) =b1×f(t) (8)
+ a2×y(t) =b1×f(t) (8)
Уравнение (8) является динамической моделью RLC цепи в виде обыкновенного линейного дифференциального уравнения.
Если в (8) перейти к изображениям по Лапласу, то получим модель цепи в виде передаточной функции:
y(p) = W(p) ×f(p) = 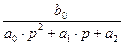 ×f(p) (9)
×f(p) (9)
В таблицах 2 и 3 приводятся зависимости между параметрами передаточной функции
W(p) = 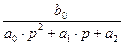 (10)
(10)
и параметрами переходных, весовых и частотных функций.
Содержание лабораторной работы
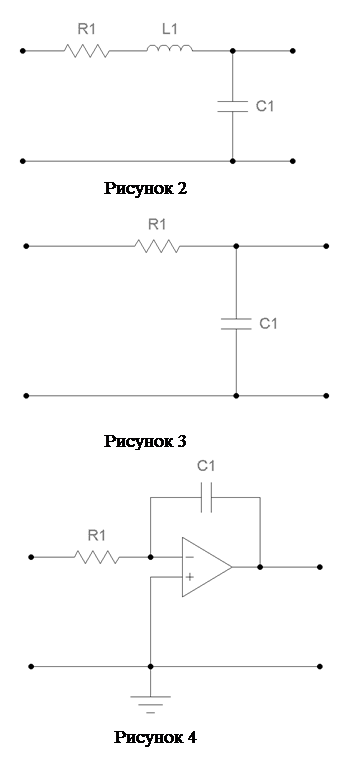 |
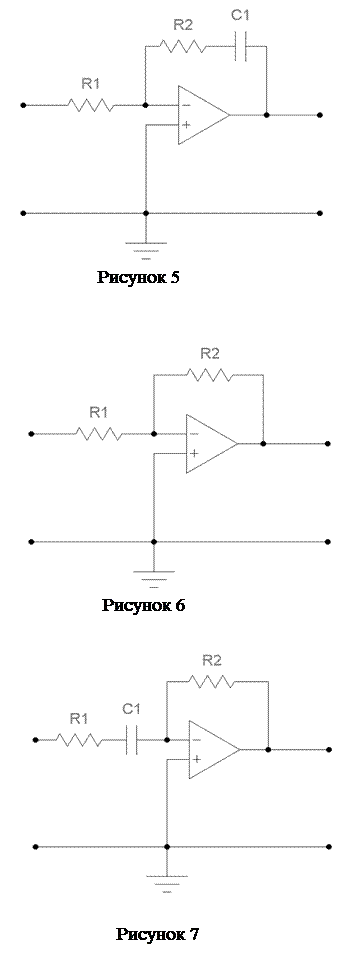
В ходе выполнения лабораторной работы необходимо снять переходную функцию и частотные характеристики динамических звеньев, приведенных на рисунках 2-7. Параметры элементов устанавливаются в соответствии с вариантом, назначенным преподавателем из таблицы 4.
Примечание:
В качестве входных и выходных переменных в динамических звеньях принимается напряжение.
При составлении уравнений, описывающих процессы в операционном усилителе, принимаем следующие допущения:
- входное сопротивление операционного усилителя бесконечно;
- коэффициент передачи операционного усилителя без обратной связи бесконечен;
- параметры операционного усилителя не зависят от частоты (скорости нарастания) преобразуемого сигнала;
- операционный усилитель – линейное звено без насыщения (достигается ограничением амплитуды входного сигнала).
Принятые допущения позволяют выводить передаточные функции динамических звеньев, выполненных на операционных усилителях, по формуле:
Wоу(p) = 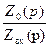 ,
,
где Z0 — комплексное сопротивление обратной связи,
Zвх — комплексное сопротивление входной цепи.
Таблица 4
Значение параметров элементов исследуемых звеньев
| № | R1, кОм | R2, кОм | C1, мкФ | L1, Гн |
Продолжение таблицы 4
| № | R1, кОм | R2, кОм | C1, мкФ | L1, Гн |
Дата добавления: 2014-12-09; просмотров: 3682;
