Краткие теоретические сведения.
| Шифр учащегося | Задание 1 | Задание 2 | Задание 3 | Задание 4 | Задача 1 | Задача 2 |
| 11з-1, 12з-6 | ||||||
| 11з-2, 12з-18 | ||||||
| 11з-3, 12з-4 | ||||||
| 11з-4, 12з-13 | ||||||
| 11з-5, 12з-11 | ||||||
| 11з-6, 12з-17 | ||||||
| 11з-7, 12з-3 | ||||||
| 11з-8, 12з-15 | ||||||
| 11з-9, 12з-8 | ||||||
| 11з-10, 12з-7 | ||||||
| 11з-11, 12з-12 | ||||||
| 11з-12, 12з-1 | ||||||
| 11з-13, 12з-9 | ||||||
| 11з-14, 12з-14 | ||||||
| 11з-15, 12з-5 | ||||||
| 11з-16, 12з-2 | ||||||
| 11з-17, 12з-16 | ||||||
| 11з-18, 12з-10 |
ИССЛЕДОВАНИЕ СВОЙСТВ И ХАРАКТЕРИСТИК ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
Цель работы
Изучение основных характеристик динамических звеньев. Исследование взаимосвязей между параметрами типовых динамических звеньев и их характеристиками.
Лабораторная работа предназначена для студентов, изучивших теоретические основы электротехники и умеющих работать на персональном компьютере в среде операционных систем Windows.
Для анализа предлагается рассмотреть модели различных динамических звеньев в среде прикладной программы EWB.
Перед выполнением лабораторной работы необходимо изучить прикладной пакет программ EWB по методическим пособиям один и два.
Модели исследуемых динамических звеньев выполнены на пассивных и активных элементах электрических цепей. Задающие воздействия подаются на вход исследуемых звеньев с источников типовых сигналов. Входной и выходной сигналы измеряются и отображаются с помощью вольтметров, бодеплотера и осциллографа.
Краткие теоретические сведения
Элементы линейных и линеаризированных систем автоматического регулирования (САР) описываются дифференциальными уравнениями или передаточными функциями. Такие элементы САР принято называть динамическими звеньями.
Если порядок дифференциального уравнения или полиномов передаточных функций не превышает второго порядка, то такие динамические звенья называются типовыми.
Из курса алгебры известно, что полином любого порядка можно разложить на простые множители. То есть любую САР можно представить в виде последовательного соединения типовых звеньев. С другой стороны, реальные звенья САР с самой разнообразной физической основой (электронные, механические, гидравлические, электромеханические и т.п.) и разным конструктивным исполнением могут иметь одинаковые математические описания и относятся к типовым динамическим звеньям. Поэтому знания характеристик типовых динамических звеньев необходимы для освоения методов анализа и синтеза САР.
Все линейные типовые динамические звенья по виду уравнений статики разделяют на три группы: позиционные звенья, интегрирующие и дифференцирующие.
Позиционные звенья: апериодическое первого и второго порядков, пропорциональное, колебательное, консервативное и чистого запаздывания – характеризуются тем, что в каждом из них, кроме консервативного, при подаче на вход постоянной величины с течением времени устанавливается постоянное значение выходной величины.
Интегрирующие звенья: идеальное интегрирующее, интегрирующее с запаздыванием и изодромное характеризуются тем, что в каждом из них при постоянном входном воздействии в установившемся режиме выходная величина неограниченно растет.
Дифференцирующие звенья: идеальное дифференцирующее, дифференцирующее с замедлением характеризуются тем, что реагируют только на изменение входной величины, то есть в установившемся режиме выходная величина таких звеньев должно стремиться к нулю.
Для исследования свойств САР или отдельных динамических звеньев (в том числе и типовых) применяются типовые частотные и временные воздействия.
В таблице 1 приводятся математические модели типовых динамических звеньев.
Таблица 1
| № п.п. | Тип звена | Передаточная функция | |
| Позиционные | Безынерционные | W(p)=k | |
| Апериодическое 1-го порядка | 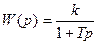
| ||
| Апериодическое 2-го порядка | 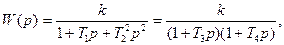
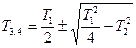 (T1 > T2) (T1 > T2)
| ||
| Колебательное | 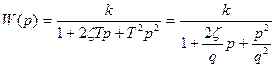
| ||
| Консервативное | 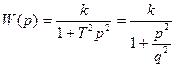
| ||
| Интегрирующие | Идеальное интегрирующее | 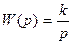
| |
| Интегрирующее с замедлением | 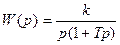
| ||
| Изодромное | 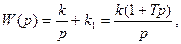
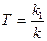
| ||
| Дифференцирующие | Идеальное дифференцирующее | W(p)=kp | |
| Дифференцирующее с замедлением |
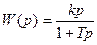
|
Временные характеристики: Под временными характеристиками в общем случае понимается графическое изображение процесса изменения выходной величины в функции времени при переходе системы (или звена) из одного равновесного состояния в другое в результате поступления на вход системы (или звена) некоторого типового воздействия.
Так как дифференциальное уравнение системы (или звена) тоже определяет изменение выходной величины в функции времени при некоторых начальных условиях, то временная характеристика изображает собой решение дифференциального уравнения для принятого типового воздействия и, следовательно, полностью характеризует динамические свойства системы (или звена).
Так как временные характеристики могут быть получены не только путем решения дифференциального уравнения, но и экспериментально, то возможность определения динамических свойств системы (или звена) по временной характеристике имеет исключительно важное практическое значение, поскольку в этом случае не требуется выводить и решать дифференциальное уравнение.
В качестве типовых воздействий наиболее широкое применение находятединичное ступенчатое и единичное импульсное воздействия.
Математическое выражение единичного ступенчатого воздействия может быть записано в виде:
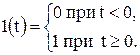
Под единичным импульсным воздействием понимается предельно короткий импульс:
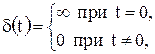
площадь которого равна единице, то есть
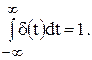
Выражение для единичного импульса δ(t) в математике принято называть дельта-функцией.
Графическое изображение реакции системы или элемента системы (например, динамического звена) на единичное ступенчатое воздействие называетсяпереходной характеристикой.
Аналитическое выражение переходной характеристики обозначается h(t) и называется переходной функцией.
Графическое изображение реакции системы на единичное импульсное воздействие называетсяимпульсной переходной характеристикой.
Аналитическое выражение импульсной переходной характеристики обозначается ω(t) и называется импульсной переходной функцией или весовой функцией (функцией веса).
При практических расчетах наиболее широкое применение находит временная характеристика в виде переходной характеристики, так как ее достаточно просто получить экспериментально и, кроме того, определяемый ею переходный процесс часто возникает при включениях и изменениях задающего воздействия.
Частотные характеристики. Если на вход линейной непрерывной системы (или отдельного звена) подать синусоидальное (гармоническое) воздействие с постоянной амплитудой Авх и частотой w: Х(t)=Авх sinωt, то в установившемся режиме (после затухания переходного процесса) на выходе также возникает синусоидальное колебание Y(t)=Авыхsin(ωt+φ) c той же частотой w, но с амплитудой Авых и сдвигом по фазе относительно входных колебаний на угол j. Синусоидально изменяющиеся величины удобно изображать с помощью комплексных амплитуд.
Подавая на вход системы гармонические колебания с постоянной амплитудой, но различными частотами, на выходе системы тоже получаем гармонические колебания с теми же частотами, но различными амплитудами и фазами относительно входных колебаний.
Введем в рассмотрение отношение комплексных амплитуд выходных и входных колебаний:
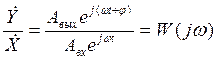
Для анализа частотных характеристик принято использовать частотную передаточную функцию. Функция W(jω) называетсячастотной передаточной и может быть получена чисто формально, без каких-либо вычислений, путем замены в выражении передаточной функции переменной р на переменную jω.
В различных формах записи функцию W(jω) можно представить в следующем виде:
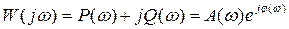
где Р(ω) = Re[W(jω)] и Q(ω) = Im[W(jω)] - действительная и мнимая части частотной передаточной функции.
А(ω) = Авых/Авх и φ(ω) - модуль и аргумент частотной передаточной функции.
В теории автоматического управления принято рассматривать следующие виды частотных характеристик:
– амплитудно-фазовая частотная характеристика (АФЧХ);
– вещественная частотная характеристика Р(ω);
– мнимая частотная характеристика Q(ω);
– амплитудно-частотная характеристика А(ω);
– фазово-частотная характеристика φ(ω).
Между всеми частотными характеристиками существует непосредственная связь:
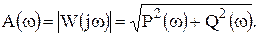
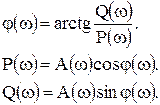
В практических расчетах чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе (асимптотические логарифмические амплитудно-частотные характеристики ЛАЧХ и асимптотические логарифмические фазово-частотные характеристики ЛФЧХ), что позволяет в значительной степени сократить объем вычислительных работ.
Логарифмической единицей усиления или ослабления мощности сигнала при прохождении его через какое-либо устройство в технике принят Бел это десятичный логарифмом отношения величины мощности на входе Рвых к мощности на входе Рвх. Так как мощность сигнала пропорциональна квадрату его амплитуды, получим:
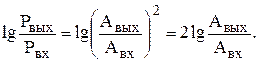
Бел является достаточно крупной единицей усиления (ослабления) мощности (увеличению мощности в 10 раз соответствует 1Б), поэтому за единицу измерения принят децибел 1дБ=0,1Б.
С учетом этого можно записать:
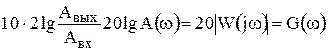
Величина логарифма амплитудной частотной характеристики, выраженная в децибелах G(ω)=20×1gA(ω).
Таким образом, изменению отношения двух амплитуд в 10 раз соответствует изменение усиления на 20 дБ, в 100 раз - на 40 дБ, в 1000 раз - на 60 дБ и т.д.
За единицу измерения частоты используется логарифмическая единица декада. Декадой называется интервал частот между какой-либо величиной частоты и ее десятикратным значением.
В логарифмическом масштабе частот отрезок в одну декаду не зависит от частоты и имеет длину, равную
lg10 ω -lg ω = lg10 = L
Рассмотрим некоторые типовые звенья и их характеристики.
Пропорциональное (безинерционное) звено.
Описывается уравнением и имеет передаточную функцию:
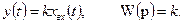
Параметр k называется коэффициентом передачи.
Частотные и временные функции звена:
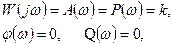
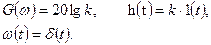
Примерами таких звеньев могут служить механические связи, электронные усилители сигналов на низких частотах и др.
Дата добавления: 2014-12-09; просмотров: 1292;
