Экономическая информация и информационные технологии

Экономическая информация – это преобразованная и обработанная совокупность сведений, отражающая состояние и ход экономических процессов. Экономическая информация циркулирует в экономической системе и сопровождает процессы производства, распределения, обмена и потребления материальных благ и услуг. Экономическую информацию следует рассматривать как одну из разновидностей управленческой информации.

Экономическая информация может быть:

· управляющая (в форме прямых приказов, плановых заданий и т.д.);

· осведомляющая (в отчетных показателях, выполняет в экономической системе функцию обратной связи).

Информацию можно рассматривать как ресурс, аналогичный материальным, трудовым и денежным ресурсам. Информационные ресурсы – совокупность накопленной информации, зафиксированной на материальных носителях в любой форме, обеспечивающей ее передачу во времени и пространстве для решения научных, производственных, управленческих и других задач.

Информационные технологии

Сбор, хранение, обработка, передача информации в числовой форме осуществляется с помощью информационных технологий. Особенностью информационных технологий является то, что в них и предметом и продуктом труда является информация, а орудиями труда – средства вычислительной техники и связи.

Основная цель информационных технологий - производство необходимой пользователю информации в результате целенаправленных действий по ее переработке.

Известно, что информационная технология – это совокупность методов, производственных и программно-технологических средств, объединенных в технологическую цепочку, обеспечивающую сбор, хранение, обработку, вывод и распространение информации.

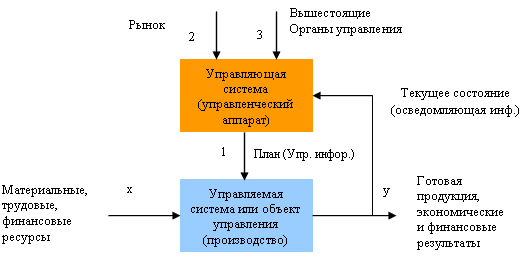
Система управления предприятием функционирует на базе информации о состоянии объекта, его входов Х (материальные, трудовые, финансовые ресурсы) и выходов Y (готовая продукция, экономические и финансовые результаты) в соответствии с поставленной целью (обеспечить выпуск необходимой продукции).

Управление осуществляется путем подачи управленческого воздействия 1 (план выпуска продукции) с учетом обратной связи - текущего состояния управляемой системы (производства) и внешней среды (2, 3) - рынок, вышестоящие органы управления.

Назначение управляющей системы - формировать такие воздействия на управляемую систему, которые побуждали бы последнюю принять состояние, определяемое целью управления.

Применительно к промышленному предприятию с некоторой долей условности можно считать, что цель управления - это выполнение производственной программы в рамках технико-экономических ограничении; управляющие воздействия - это планы работ подразделении, обратная связь данные о ходе производства: выпуске и перемещении изделии, состоянии оборудования, запасах на складе и т.д.

Очевидно, что планы и содержание обратной связи - не что иное, как информация. Поэтому процессы формирования управляющих воздействий как раз и являются процессами преобразования экономической информации. Реализация этих процессов и составляет основное содержание управленческих служб, в том числе экономических. К экономической информации предъявляются следующие требования: точность, достоверность, оперативность.

Точность информации обеспечивает ее однозначное восприятие всеми потребителями. Достоверность определяет допустимый уровень искажения как поступающей, так и результатной информации, при котором сохраняется эффективность функционирования системы. Оперативность отражает актуальность информации для необходимых расчетов и принятия решений в изменившихся условиях.

Меры информации. Для автоматизации работы ЭВМ с информацией, относящейся к различным типам, очень важно унифицировать их форму представления – для этого обычно используется прием кодирования.

Иначе говоря, это правило, описывающее отображение одного набора знаков в другой набор знаков. Тогда отображаемый набор знаков называется исходным алфавитом, а набор знаков, который используется для отображения, – кодовым алфавитом, или алфавитом для кодирования. При этом кодированию подлежат как отдельные символы исходного алфавита, так и их комбинации. Аналогично для построения кода используются как отдельные символы кодового алфавита, так и их комбинации.

В качестве примера можно привести систему записи математических выражений, азбуку Морзе, морскую флажковую азбуку, систему Брайля для слепых и др.

Какой же язык, какой способ кодирования применить в информатике? Ответ на этот вопрос нашел Клод Элвуд Шеннон(Claude Elwood Shannon, 1916-2001) – американский математик и электротехник. В своей диссертации, защищенной в 1940 году, он доказал, что работу переключателей и реле в электрических схемах можно представить посредством алгебры, изобретенной в середине XIX века английским математиком Джорджем Булем. "Просто случилось так, что никто другой не был знаком с этими обеими областями одновременно!" – так скромно Шеннон объяснил причину своего открытия.

Количество информации определяется так же через понятие энтропии системы. Энтропия Больцмана – это мера беспорядка. При равновероятном распределении параметров системы (например, направлений движения молекул) энтропия максимальна! При упорядочивании системы (задание определенного направления движения) энтропия уменьшается.

Текст с максимальной энтропией – равновероятное распределение букв – бессмысленное содержание – 0 информации. Теперь пусть в неком информационном сообщении (в SMS – сообщении) случайным образом из-за помех некоторые буквы были заменены. Информация – это нужные, верные, достоверные сигналы –I. Неверные буквы – это шум, беспорядок –H.

H+I=1

Пусть P_i – это вероятность того, что система находится в состоянии i. (вероятность того, что буква будет, например «В»). Количество возможных состояний N. Тогда энтропия по Шеннону – это мера недостающей информации которую можно записать формулой.Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений.

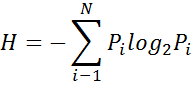
Рассмотрим такой подход к определению понятия информация более подробно. В окружающей действительности достаточно часто встречаются ситуации, когда существует некоторое количество событий, каждое из которых может произойти с определенной вероятностью. Рассмотрим это на простейшем примере «Бросание монеты». Если монету бросить, то выпадает одно из двух событий : «орел» или «решка».

Перед броском существует неопределенность, как упадет монета предсказать невозможно. После броска наступает полная определенность, так как монета находиться в определенном положении (например, «орел»).

Данный подход позволяет измерить количество информации:

N=2^I

Где: N–количество возможных информационных сообщений;

I–количество информации, которое несет одно сообщение.

Отсюда, I=log₂N

В вычислительной технике также существует своя система кодирования – она называется двоичным кодированием и основана на представлении данных последовательностью всего двух знаков: 0 и 1 (используется двоичная система счисления). Эти знаки называются двоичными цифрами, или битами (binary digital).

За единицу количества информации принимается такое количество информации, которое содержится в информационном сообщении, уменьшающем неопределенность знания в два раза. Такая единица названа бит.

Если вернуться к опыту бросания монеты, то здесь неопределенность как раз уменьшается в два раза (из двух возможных событий реализуется одно), и, следовательно, полученное количество информации равно 1 биту.

В информатике наиболее употребляемой единицей измерения количества информации является байт, причем в 1 байт = 8 битов.

Компьютер оперирует числами не в десятичной системе счисления, поэтому производные единицы измерения количества информации вводятся следующим образом:

Пример 1.1 В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере?

Решение: итак, в задаче необходимо найти количество информации, которое содержит сообщение о первом выпавшем номере (шаре), т.е. необходимо найти I. Всего шаров в барабане 32, значит, всего возможных вариантов здесь 32. N = 32.

Отсюда, по формуле находим I.

I = 5 бит.

Пример 1.2. При игре в кости используется кубик с шестью гранями. Сколько бит информации получает игрок при каждом бросании кубика?

Решение: итак, в задаче необходимо найти количество информации, которое получает игрок при каждом бросании кубика, т.е. необходимо найти I. Всего граней у кубика 6, значит, всего возможных вариантов здесь 6. N = 6.

Отсюда, по формуле (2.3) находим I, используя также таблицу логарифмов.

I = 2,585 бит.