Методы дискретной математики (теория множеств, математическая логика, математическая лингвистика, семиотика, графы).

Теоретико – множественные, логические, лингвистические, семиотические, графические методы возникали как самостоятельные направления и первоначально развивались независимо друг от друга. В последующем обобщающий аппарат теоретико-множественных представлений оказался столь удобным, что позволил объединить эти представления в единую область – дискретную математику.

В то же время, для того, чтобы правильно применять методы, полезно кратко рассмотреть особенности и возможности всех названных групп методов.

Теоретико – множественные представления.

Они базируются на таких понятиях, как множество, элементы множества, отношения на множествах. Понятие «множество» относится к числу интуитивно постигаемых понятий, которым трудно дать определение. Это понятие содержательно эквивалентно понятиям совокупность, собрание, ансамбль, коллекция, семейство, класс и другим обобщающим понятиям.

Один из основоположников теории множеств Кантор дал такое определение: «множество – это многое, мыслимое нами как единое».

При использовании теоретико-множественных представлений, в соответствии с концепцией Кантора, можно вводить любые отношения, которые особенно наглядны применительно к операциям объединения, пересечения и дополнения (отрицания), когда они представлены в виде диаграмм (кругов) Эйлера – Венна.

Теории, развивающиеся на базе теоретико-множественных представлений, первоначально использовали отношения, подобные функциям алгебры логики, и, в первую очередь, бинарной алгебры логики Буля. В большинстве работ эти представления излагаются на примере теории чисел, для развития которой достаточно основных элементарных отношений: принадлежности ( 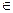, 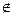), включения ( 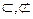), объединения ( 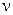), пересечения (Ώ), отрицания ( ).

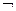По мере приложения теоретико-множественных представлений к более сложным проблемам отношения начинают заимствоваться из математической лингвистики (которую теория множеств, в свою очередь, помогает развивать), а при отображении особо сложных проблемных ситуаций с неопределенностью формируемую или исследуемую систему отображают множествами с отношениями произвольного типа (так, при применении теоретико-множественных представлений в ситуационном моделировании используются отношения «быть над», « быть под», «находиться рядом» и т. п., которые допустимо обозначить в разрабатываемом на этой основе языке моделирования произвольными символами, удобными для ЛПР).

Множества можно преобразовать путем установления взаимоотношений между элементами разных исходных множеств. Из двух или нескольких множеств можно сформировать новое множество. Так, из множеств «женихи» и «невесты» в ЗАГСе путем проведения соответствующей операции (процедуры регистрации брака) формируется множество «семьи», которое состоит из принципиально новых элементов: мужья и жены.

Важным понятием для использования теоретико-множественных представлений является понятие континуума (от латинского continuum - непрерывный) – обобщающего множества (как бы единого непрерывного пространства), в рамках которого осуществляются операции над множествами. В случае моделирования развивающихся систем континуум постоянно видоизменяется.

Благодаря тому, что, в соответствии с первоначальной концепцией Кантора, при применении теории множеств допустимо введение любых, произвольных отношений, теоретико – множественные представления стали использоваться как обобщающий язык при сопоставлении различных направлений математики и других дисциплин.

Теоретико-множественные представления явились основой для возникновения ряда новых направлений и для развития существующих, таких как теория чисел, комбинаторика, топология, теории «размытых» множеств, а также создания информационно – поисковых языков, языков автоматизации моделирования, математической теории систем.

Использование теоретико - множественных представлений при моделировании систем позволяет организовать взаимодействие и взаимопонимание между специалистами различных областей знаний. Это достигается путем описания системы на языке моделирования, базирующемся на теоретико – множественных представлениях.