Методические указания к решению задач К 2.9, К 2.10

В задаче 2.9 имеет место частный случай неплоского изгиба – косой изгиб. Неплоский изгиб вызывается нагрузками, действующими в разных плоскостях, проходящих через ось бруса. Если все нагрузки, вызывающие изгиб, действуют в одной плоскости, не совпадающей ни с одной из главных плоскостей, то такой изгиб называется косым изгибом. Главной называется плоскость, включающая в себя ось бруса и главную центральную ось сечения. При решении задач проч­ности неплоский и косой изгибы приводятся к двум плоским изгибам. Для этого нагрузку (Р, М, q) раскладывают на составляющие дейст­вующие в главных плоскостях по следующей схеме (рис. 26).

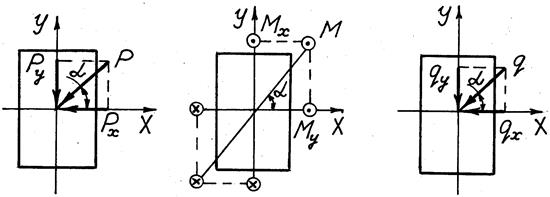
Рис. 26

Далее строят эпюры М_х и М_у, по эпюрам находят опасные сече­ния. Опасными будут сечения, где М_х или М_у или оба одновременно имеют максимальное значение. В любой точке этих сечений нор­мальные напряжения определяются формулой

,

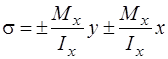(1)

Здесь х и у координаты точки, в которой определяют напряжения, взятые по абсолютной величине. Знаки перед слагаемыми берут в за­висимости того растяжение или сжатие дают М_х, М_у в этой точке (если растяжение, то плюс, если сжатие – минус). Формула (1) есть уравнение плоскости, проходящей через начало координат. След от пересечения этой плоскостью поперечного сечения будет прямой ли­нией. Напряжения на этой линии равны нулю, в связи с чем она на­зывается нейтральной (или нулевой) линией. Её уравнение

,

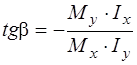(2)

где b - угол между осью Х и нейтральной линией. М_х, М_у подставляют в эту формулу со знаком плюс если они дают растяжение в первой четверти и со знаком минус – если сжатие.

При косом изгибе положение нейтральной линии можно опре­делить по формуле

,

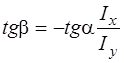(2а)

где a - угол между осью Х и плоскостью, в которой действует на­грузка.

Следует заметить, что нейтральная линия всегда проходит через те четверти, где напряжения от М_х и М_у имеют разные знаки.

Максимальные напряжения будут в точках наиболее удаленных от нейтральной линии. Эти точки находятся в тех четвертях сечения, где напряжения от М_х и М_у имеют одинаковые знаки.

Для определения положения опасных точек в сечениях произ­вольной формы их вычеркивают в масштабе, указывают направление действия М_х и М_у. По формуле (2) или (2а) определяют угол b и про­водят нейтральную линию. Проводят касательные к сечению, парал­лельные нейтральной линии. Точки касания будут наиболее удален­ными от нейтральной линии (опасными точками). Удаление опасных точек от нейтральной линии определяется путем измерения на чер­теже. Наиболее опасна та, у которой удаление больше.

Напряжения в опасных точках определяют по формуле (1).

В сечениях вписывающихся в прямоугольник (прямоугольник, двутавр, швеллер и т.д.) опасными всегда будут угловые точки, наи­более удаленные от нейтральной линии. Напряжения в этих точках можно определить по более постой формуле

,

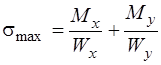Условие прочности для опасных точек имеет вид

,

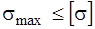Исходя из этого условия решают поставленную задачу.

На рис. 27 показано как определяют знаки напряжений в разных четвертях сечения при заданном направлении М_х и М_у, положение опасных точек, положение нейтральной линии и эпюры нормальных напряжений для поперечного сечения произвольной формы и сечения вписывающегося в прямоугольник.

Эпюра нормальных напряжений строится на базовой линии перпендикулярной нейтральной линии. Для построения эпюры про­водят касательные к сечению параллельные нейтральной линии. Из точки пересечения базовой линии с касательной проходящей через опасную точку, в которой вычислены напряжения, на касательной откладывают отрезок изображающий эти напряжения в выбранном масштабе с учетом знака. Если напряжения положительные (растяги­вающие), то их откладывают в направлении от сечения, отрицатель­ные (сжимающие) – к сечению. Через конец этого отрезка и точку пе­ресечения базовой линии с нейтральной линией проводят прямую линию до пересечения с другой касательной к сечению. Эта линия будет ограничивать эпюру «s». На поле эпюры ставят знаки, соответ­ствующие знакам изображаемых напряжений. Эпюру штрихуют пря­мыми линиями параллельными нейтральной линии. Указывают зна­чения максимальных напряжений. Около эпюры ставят знак нор­мальных напряжений «s».

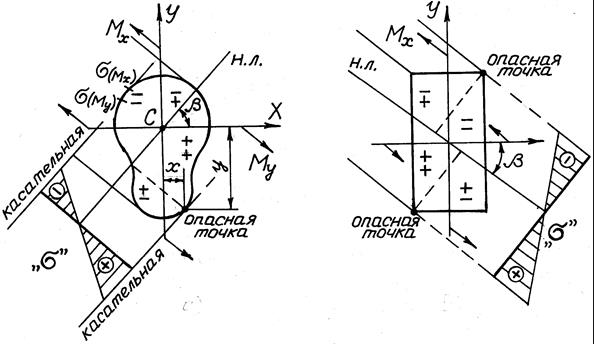
Рис. 27

Таким образом, алгоритм решения задач прочности при плоском и косом изгибах состоит из следующих шагов.

1. Разложение нагрузки на составляющие, действующие в главных плоскостях.

2. Построение эпюр внутренних силовых факторов в главных плоско­стях.

3. Определение положения опасных сечений.

4. Определение положения опасных точек в опасных сечениях. За­пись условий прочности для этих точек.

5. Ответ на вопрос задачи исходя из условий прочности.

При косом изгибе первые три шага алгоритма решения могут выпол­няться иначе (что часто оказывается проще).

1. Построение эпюр внутренних силовых факторов в плоскости дей­ст­вия нагрузки.

2. Определение положения опасных сечений.

3. Разложение внутренних силовых факторов на составляющие дей­ст­вующие в главных плоскостях.

В задаче 2.10 имеет место внецентренное сжатие. Внецентрен­ным сжатием (растяжением) называется такой случай нагружения, ко­гда сжимающая (растягивающая) сила, параллельная оси бруса, при­ложена не в центре тяжести сечения. Во всех поперечных сече­ниях бруса возникают постоянные по величине N = P, М_х = Р×у_р , М_у= Р×х_р , где х_р, у_р координаты точки приложения силы (рис. 28).

Нормальные напряжения в произвольной точке сечения опреде­ля­ются формулой

,

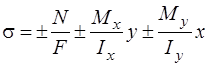(3)

где х, у – координаты точки, в которой определяются напряжения.

Уравнение (3) представляет собой уравнение плоскости не про­ходя­щей через начало координат. След от пересечения этой плоско­стью плоскости поперечного сечения будет прямой линией не прохо­дящей через начало координат. Напряжения на этой линии (ней­тральной ли­нии) равны нулю. Нейтральна линия может проходить как через по­перечное сечение, так и за его границами. Если ней­тральная линия проходит через поперечное сечение, то напряжения по разные сто­роны от нее имеют разные знаки, если нейтральная ли­ния проходит за границами сечения, то напряжения в сечении одного знака. Мак­симальные напряжения возникают в точке наиболее уда­ленной от нейтральной линии. Для нахождения положения этой точки вычерчи­вают сечение в масштабе и определяют отрезки, кото­рые нейтральная линия отсекает на осях координат, а – на оси Х и b – на оси У.

.

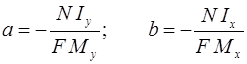Для правильного определения знаков отрезков а и b в эти формулы необходимо подставлять N, М_х, М_у со знаками напряжений, которые они дают в первой четверти. Вычисленные значения отрезков а, b от­кладывают на координатных осях с учетом знаков и через их концы проводят нейтральную линию. Если отрезки малы по сравнению с размерами сечения и их нельзя отложить с достаточной точностью, то откладывают больший из них и через его конец проводят нейтраль­ную линию под углом b к оси Х (угол b вычисляют по формуле 2). Необходимо заметить, что нейтральная линия всегда проходит через четверть противоположную той, в которой приложена сила. Проводят касательные к сечению, параллельные нейтральной линии. Точки ка­сания будут наиболее удаленными (опасными) точками. Наиболее опасной будет та точка, которая дальше удалена от нейтральной ли­нии. Напряжения в опасной точке определяют по формуле

,

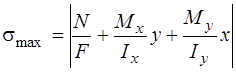где х, у – координаты точки.

Для сечений вписывающихся в прямоугольник положение опас­ной точки можно не определять, это всегда будет одна из угловых то­чек, та в которой напряжения от N, М_х, М_у имеют одинаковые знаки. Напряжения в этой точке определяются формулой

.

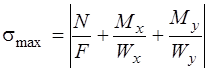Условие прочности для опасной точки имеет вид 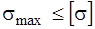. Исходя из этого условия решают поставленную задачу.

Для бруса изготовленного из метериала неодинаково сопротив­ляющегося растяжению и сжатию при внецентренном сжатии при ус­ловии обеспечения устойчивости рассматривают два условия прочно­сти – по растягивающим и сжимающим напряжениям.

По сжимающим напряжениям:

для бруса произвольного сечения

,

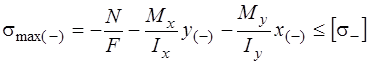для бруса с сечением вписывающимся в прямоугольник

,

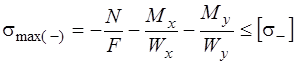где х_(-), у_(-) – координаты наиболее удаленной от нейтральной линии точки, в которой М_х и М_у, дают сжимающие напряжения; 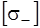– до­пускаемые напряжения на сжатие.

По растягивающим напряжениям:

для бруса произвольного сечения

,

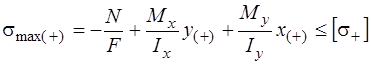для бруса с сечением, вписывающимся в прямоугольник

,

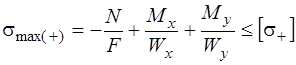где х₍₊₎, у₍₊₎ – координаты наиболее удаленной от нейтральной линии точки, в которой М_х и М_у, дают растягивающие напряжения; 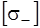– допускаемые напряжения на растяжение.

На рис .28 показано как определяется положение нейтральной линии, опасные точки и эпюры напряжений в произвольном сечении и сечении вписывающемся в прямоугольник.

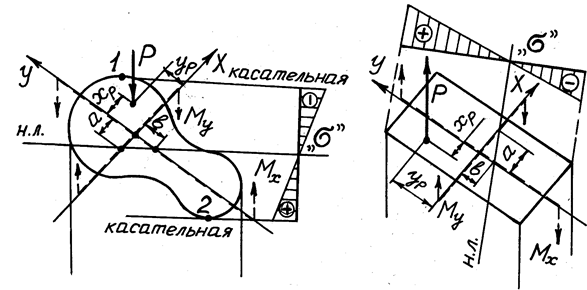Рис 28

Таким образом, алгоритм решения задач прочности при внецен­трен­ном сжатии (растяжении), состоит из следующих шагов.

1. Определение N, М_х, М_у.

2. Определение положения опасной точки (для бруса из материала не­одинаково сопротивляющегося растяжению и сжатию определяют положение двух опасных точек, одной опасной по растягивающим напряжениям, другой – по сжимающим).

3. Запись условия прочности для опасных точек.

4. Ответ на вопрос задачи исходя из условия прочности.

Если решается задача по определению размеров сечения при внецен­тренном сжатии для бруса из материала неодинаково сопро­тивляю­щегося растяжению и сжатию, то определяют размеры сече­ния от­дельно из условия прочности по растяжению и по сжатию. За ответ берут большие размеры. Если при тех же условиях определяют до­пускаемую силу, то за ответ берут меньшее ее значение.