Частоты

Наконец, для еще более наглядного представления общей конфигу­рации распределения можно строить полигоны распределения частот. Для этого отрезками прямых соединяют центры верхних сторон всех прямоугольников гистограммы, а затем с обеих сторон «замыкают» площадь под кривой, доводя концы полигонов до горизонтальной оси (частота = 0) в точках, соответствующих самым крайним значениям распределения. При этом получают следующую картину:

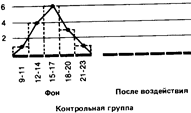
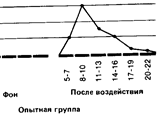
Если сравнить полигоны, например, для фоновых (исходных) значе­ний контрольной группы и значений после воздействия для опытной группы, то можно будет увидеть, что в первом случае полигон почти симметричен (т. е. если сложить полигон вдвое по вертикали, проходя­щей через его середину, то обе половины належатся Друг на друга), тогда как для экспериментальной группы он асимметричен и смещен влево (так что справа у него как бы вытянутый шлейф).

Полигон для фоновых данных контрольной группы сравнительно близок к идеальной кривой, которая могла бы получиться для бесконеч­но большой популяции. Такая кривая-кривая нормального распределе­ния-имеет колоколообразную форму и строго симметрична. Если же количество данных ограничено (как в выборках, используемых для научных исследований), то в лучшем случае получают лишь некоторое приближение (аппроксимацию) к кривой нормального распределения.

Приюжение Б

Если вы построите полигон для фоновых значений опытной группы и значений после воздействия для контрольной группы, то вы наверняка заметите, что так же будет обстоять дело и в этих случаях.