ПОНЯТИЕ ОПРОВЕРЖЕНИЯ
Опровержение — логическая операция установления ложности или необоснованности ранее выдвинутого тезиса.
Опровержение должно показать, что: 1) неправильно построено само доказательство (аргументы или демонстрация); 2) выдвинутый тезис ложен или не доказан.
Суждение, которое надо опровергнуть, называется тезисом опровержения. Суждения, с помощью которых опровергается тезис, называются аргументами опровержения.
Существуют три способа опровержения: 1) опровержение тезиса (прямое и косвенное); 2) критика аргументов; 3) выявление несостоятельности демонстрации.
I. Опровержение тезиса (прямое и косвенное)
Опровержение тезиса осуществляется с помощью следующих трех способов (первый — прямой способ, второй и третий — косвенные способы).
1. Опровержение фактами — самый верный и успешный способ опровержения. Ранее подробно говорилось о роли подбора фактов, о методике оперирования ими; все это должно учитываться и в процессе опровержения фактами, противоречащими тезису. Должны быть приведены действительные события, явления, статистические данные, результаты эксперимента, свидетельские показания, научные данные, которые противоречат тезису, т. е. опровергаемому суждению. Например, чтобы опровергнуть тезис «На Венере возможна органическая жизнь», достаточно привести такие данные: температура на поверхности Венеры 470—480 градусов Цельсия, а давление 95—97 атмосфер. Эти данные свидетельствуют о том, что жизнь на Венере в известных нам формах невозможна.
2. Установление ложности (или противоречивости) следствии, вытекающих из тезиса. Доказывается, что из данного тезиса вытекают следствия, противоречащие истине. Этот прием называется «сведение к абсурду» (reductio ad absurdum).
Как уже отмечалось, в классической двузначной логике метод сведения к абсурду выражается в виде формулы где
F — противоречие или ложь. 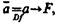
В более общей форме принцип сведения (приведения) к абсурду выражается такой формулой: 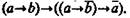
3. Опровержение тезиса через доказательство антитезиса. По отношению к опровергаемому тезису (суждению а) выдвигается противоречащее ему суждение (т. е. не-а)и суждение не-а (антитезис) доказывается. Если антитезис истинен, то тезис ложен, третьего не дано.
Например, надо опровергнуть широко распространенный тезис «Все собаки лают» (суждение А, общеутвердительное). Для суждения А противоречащим будет суждение О — частноотрицательное: «Некоторые собаки не лают». Для доказательства последнего достаточно привести несколько примеров или хотя бы один пример: «Собаки у пигмеев никогда не лают». Итак, доказано суждение О. В силу закона исключенного третьего если О истинно, то А ложно. Следовательно, тезис опровергнут.
Дата добавления: 2014-12-08; просмотров: 1021;
