Условно-категорические умозаключения
Условно-категорическое умозаключение — это такое дедуктивное умозаключение, в котором одна из посылок — условное суждение, а другая — простое категорическое суждение.
Оно имеет два правильных модуса, дающих заключение, с необходимостью следующее из посылок.
I. Утверждающий модус (modus ponens).
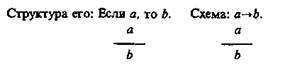
Формула (1): 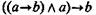 — является законом логики.
— является законом логики.
Можно строить достоверные умозаключения от утверждения основания к утверждению следствия. Приведем два примера.
Если ты хочешь наслаждаться искусством, то ты должен быть художественно образованным человеком.
Ты хочешь наслаждаться искусством.
____________________________________
Ты должен быть художественно образованным человеком.
Для построения другого примера воспользуемся интересным высказыванием великого русского педагога К. Д. Ушинского: «Если человек избавлен от физического труда и не приучен к умственному, зверство овладевает им»2 . Использовав это высказывание, построим условно-категорическое умозаключение.
Если человек избавлен от физического труда и не приучен к умственному, то им овладевает зверство.
Этот человек избавлен от физического труда и не приучен к умственному.
_________________________________________
Этим человеком овладевает зверство.
Любое использование правил в русском языке, математике, физике, химии и других школьных дисциплинах основано на утверждающем модусе, дающем достоверное заключение, поэтому в практике мышления он находит самое широкое применение.
Если этот металл натрий, то он легче воды.
Данный металл — натрий.
____________________________
Данный металл легче воды.
II. Отрицающий модус (modus tollens).
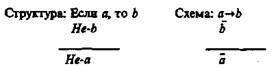
Формула (2): 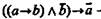 — также является законом логики
— также является законом логики
(это можно доказать с помощью таблицы).
Можно строить достоверные умозаключения от отрицания следствия к отрицанию основания.
Приведем два примера.
Если река выходит из берегов, то вода заливает прилегающие территории.
Вода реки не залила прилегающие территории.
____________________________
Река не вышла из берегов.
Для построения второго условно-категорического умозаключения воспользуемся следующим высказыванием: «...тот мерзок, кто ярится, если чужой он доблести свидетель» (Данте). Умозаключение построено так:
Если человек при виде чужой доблести ярится, то он мерзок.
Этот человек не является мерзким.
__________________________________
Этот человек при виде чужой доблести не ярится.
Условно-категорическое умозаключение может давать не только достоверное заключение, но и вероятное.
Первый модус, не дающий достоверное заключение.

Формула (3): 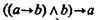 — не является законом логики.
— не является законом логики.
Нельзя получить достоверное заключение, идя от утверждения следствия к утверждению основания. Например, в умозаключении
Если бухта замерзла, то суда не могут входить в бухту.
Суда не могут входить в бухту.
_____________________________
Вероятно, бухта замерзла.
заключение будет лишь вероятным суждением, т. е., вероятно, бухта замерзла, но возможно, что дует сильный ветер или бухта заминирована либо существует другая причина, по которой суда не могут входить в бухту.
Вероятное заключение получится и в таком умозаключении:
Если данное тело — графит, то оно электропроводно.
Данное тело электропроводно.
_____________________________
Вероятно, данное тело — графит.
Второй модус, не дающий достоверное заключение.
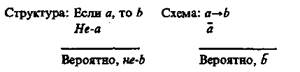
Формула (4): 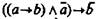 — не является законом логики.
— не является законом логики.
Нельзя получить достоверное заключение, идя от отрицания основания к отрицанию следствия. Например:
Если человек имеет повышенную температуру, то он болен.
Этот человек не имеет повышенной температуры.
_____________________________________
Вероятно, этот человек не болен.
Люди иногда допускают логические ошибки при построении умозаключений. Они могут умозаключать так:
Если тело подвергнуть трению, то оно нагреется.
Тело не подвергли трению.
_____________________
Тело не нагрелось.
Но заключение здесь только вероятное, а не достоверное, ибо тело могло нагреться по какой-либо другой причине (от солнца, в печи и т. д.).
Заметим, что приведения такого рода примеров вполне достаточно для того, чтобы показать, что формы умозаключений, выражаемые формулами (3) и (4), неправильны. Но никакое количество примеров применения форм, соответствующих формулам (1) и (2), не в состоянии — если мы оперируем только примерами — обосновать их логическую правильность. Для такого обоснования требуется уже некоторая логическая теория. Такая теория, фактически отсутствующая в традиционной логике, содержится в алгебре логики. Если формула, в которой конъюнкция посылок и предполагаемое заключение соединены знаком импликации, не является тождественно-истинной, т. е. не выражает закона логики, то в умозаключении заключение не является достоверным. В таблице истинности (табл. 9) видно, что столбцы, соответствующие формулам (1) (modus ponens) и (2) (modus tollens), состоят из одних знаков «И» («истинно»); следовательно, формулы (1) и (2) выражают законы логики, а это означает, что modus ponens и modus tollens представляют собой логически правильные формы умозаключений.
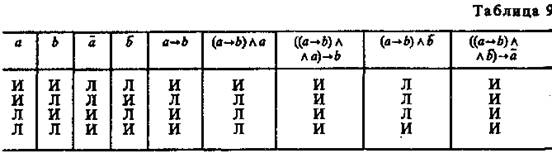
Таблицу для неправильных модусов предоставляем построить читателю. В ней наряду со знаками «И» мы увидим и знаки «Л» («ложь»), а это значит, что выражения 
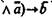 не являются тождественно-истинными высказываниями, т. е. законами логики.
не являются тождественно-истинными высказываниями, т. е. законами логики.
Если умозаключение строится от утверждения следствия к утверждению основания, то вследствие множественности причин, из которых может вытекать одно и то же следствие, можно прийти к ложному заключению. Например, выясняя причину заболевания человека, надо перебрать все возможные причины: простудился, переутомился, был в контакте с бациллоносителем и т. д.
Дата добавления: 2014-12-08; просмотров: 1110;
