Тема 8. Фиктивные переменные во множественной регрессии. Их использование для моделирования сезонных колебаний
| № п/п | Вид самостоятельной работы | Количество часов, отводимых на данный вид работы | Формируемые и развиваемые компетенции | ||
| очная форма обучения | очно-заочная форма обучения | заочная форма обучения | |||
| Изучение электронных учебно-методических материалов | 0,5 | ПК-1,2,4,6,8,12. | |||
| Изучение научной и учебно-методической литературы (см. список основной литературы) | 0,5 | ПК-1,2,4,6,8,12. | |||
| Решение тестов к Теме 8. | ПК-1,2,4,6,8,12. | ||||
| Подготовка к семинару | 0,5 | ПК-1,2,4,6,8,12. |
4. Семестровое задание для самостоятельной работы.
4. 1.Задания на контрольную работу и методические указания по их выполнению
Выполняя задания, студенты закрепляют теоретический материал, учатся осуществлять анализ и обработку данных, необходимых для решения поставленных экономических задач (ПК-1,2,4), на основе описания экономических процессов и явлений строить стандартные теоретические и эконометрические модели, анализировать и содержательно интерпретировать полученные результаты (ПК-6); выявлять тенденции изменения социально-экономических показателей (ПК-8); получают навыки использования для решения практических задач современные технические средства и информационные технологии (ПК-12).
Дисциплина «Эконометрика» изучается в течении одного семестра, в период которого каждый студент должен выполнить контрольную работу по узловым темам, состоящую из трех частей : парная линейная регрессия (ПК-1,2,4,12) , множественная регрессия ( ПК- 4,6,8,12) , временные ряды (ПК-8,12). Студенты заочной формы обучения выполняют работы самостоятельно в межсеместровый период и сдают их во время сессии. Трудоёмкость семестрового задания составляет 12 часов.
При решении рекомендуется использовать ППП MS Excel, т.к. он присутствует в подавляющем большинстве персональных компьютеров.
Контрольную работу следует выполнять на листах бумаги формата А4 (листы заполняются с одной стороны). На титульном листе должны быть указаны фамилия, полное имя и номер группы. Распечатка компьютерных расчетов включается в отчет как приложение. Две первые контрольные работы посвящены регрессионному анализу, который является одним из наиболее распространённых методов обработки экспериментальных данных при изучении экономических явлений. Вариант задания соответствует последней цифре номера зачетной книжки. Данные каждого варианта третьей контрольной работы определяются параметрами р1 и р2. р1 – число букв в полном имени студента, р2 – число букв в фамилии студента.
При выполнении контрольных заданий 1 и 2 следует придерживаться следующих этапов построения регрессионной модели.
Пример 1.
Исследуем зависимость розничного товарооборота от числа занятых . Товарооборот как результирующий признак обозначим через y, а среднесписочное число работников как независимую переменную (фактор) обозначим через х.
| номер наблюдения | x | y | x*y | x² | x-x̄ | y-ȳ | ŷ | (x-x̄)(y-ȳ) | (x-x̄)² | (y-ȳ)² | ŷ-ȳ | (ŷ-ȳ)² | y-ŷ | (y-ŷ)² |
| 0,5 | 36,5 | -40 | -0,7 | 0,43 | 0,49 | -0,769 | 0,5921 | 0,069 | 0,0048 | |||||
| 0,7 | 59,5 | -28 | -0,5 | 0,66 | 0,25 | -0,538 | 0,2901 | 0,038 | 0,0014 | |||||
| 0,9 | 91,8 | -11 | -0,3 | 0,98 | 3,3 | 0,09 | -0,211 | 0,0447 | -0,088 | 0,0078 | ||||
| 1,1 | 126,5 | -0,1 | 1,23 | -0,2 | 0,01 | 0,038 | 0,0014 | -0,138 | 0,0191 | |||||
| 1,4 | 170,8 | 0,2 | 1,37 | 1,8 | 0,04 | 0,173 | 0,0299 | 0,026 | 0,0007 | |||||
| 1,4 | 176,4 | 0,2 | 1,45 | 2,6 | 0,04 | 0,250 | 0,0625 | -0,050 | 0,0025 | |||||
| 1,7 | 227,8 | 0,5 | 1,60 | 10,5 | 0,25 | 0,404 | 0,1632 | 0,096 | 0,0092 | |||||
| 1,9 | 279,3 | 0,7 | 1,85 | 23,8 | 0,49 | 0,654 | 0,4278 | 0,045 | 0,0021 | |||||
| Итого | 9,6 | 1168,6 | 83,8 | 1,66 | 1,6121 | 0,0478 | ||||||||
| Среднее значение | 1,2 | 0,0079 |
Определим величину коэффициента корреляции.
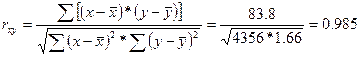
Величина линейного коэффициента корреляции rxy=0.985 показывает сильную положительную линейную связь рассматриваемых признаков : розничного товарооборота и среднесписочного числа работников.
Представим у как линейную функцию х. Параметры модели определим методом наименьших квадратов.
Определим коэффициент уравнения регрессии b.
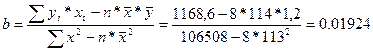
Коэффициент b показывает, что увеличение среднесписочной численности на одного человека приводит к увеличению товарооборота в среднем на 19,24 тыс.руб.
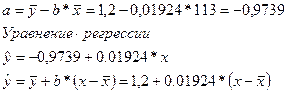
Рассчитаем теоретическое значение  для 8 магазинов. Результаты занесем в таблицу.
для 8 магазинов. Результаты занесем в таблицу.
Возможен сравнительный анализ работы магазинов на основании анализа столбца (у-  ). Следует обратить внимание на магазины с отрицательными отклонениями, т.е. 3,4,6.
). Следует обратить внимание на магазины с отрицательными отклонениями, т.е. 3,4,6.
Определим коэффициент детерминации, который характеризует долю вариации зависимой переменной, объясненной с помощью данного уравнения и тем самым является оценкой качества модели.
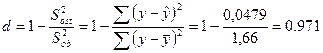
В исследуемой ситуации 97,1% общей вариабельности розничного товарооборота объясняется изменением числа работников. На все остальные факторы приходится 2,9% вариабельности.
Для определения статистической значимости уравнения регрессии в целом используется распределение Фишера.
Fрасч >Fтабл, делается вывод о существенности связи.

Поскольку 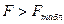 при 5% уровне значимости можно сделать вывод о значимости уравнения регрессии.
при 5% уровне значимости можно сделать вывод о значимости уравнения регрессии.
Для определения статистической значимости коэффициентов линейной регрессии в целом используется распределение Стьюдента. Если расчетное значение tb по модулю не превосходит табличного значения, то принимается нулевая гипотеза об отсутствии значимой зависимости, в противном случае нулевую гипотезу отклоняем.
Значимость коэффициента регрессии b может быть проверена с помощью своего отношения к своему стандартному отклонению.
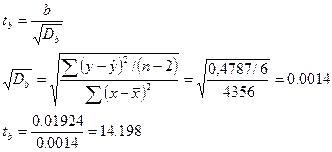 -стандартная ошибка коэффициента регрессии
-стандартная ошибка коэффициента регрессии
Табличное значение критерия Стьюдента определяется с помощью функции СТЬЮДРАСПОБР.
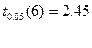
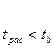
Гипотезу о несущественности коэффициента регрессии можно отклонить.
Точечное прогнозирование.
Пусть намечается открытие магазина такого же типа, где среднесписочное число работников Х=140 человек. Тогда ожидаемый объем товарооборота 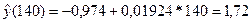 млн.руб.
млн.руб.
Вычислим стандартную ошибку предсказания
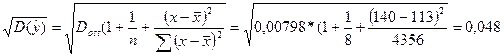
Интервальное прогнозирование.
Доверительный интервал для прогнозируемого значения.
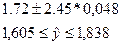
Заключение.
Изучена зависимость розничного товарооборота от числа занятых.
На этапе спецификации была выбрана парная линейная регрессия. Оценены её параметры методом наименьших квадратов. Статистическая значимость уравнения проверена с помощью коэффициента детерминации и критерия Фишера. Установлено, что в исследуемой ситуации 97,1% общей вариабельности розничного товарооборота объясняется изменением числа работников. Установлено также, что параметры модели статистически значимы. Возможна экономическая интерпретация параметров модели,- увеличение среднесписочной численности на одного человека приводит к увеличению товарооборота в среднем на 19,24 тыс.руб. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. В магазине, где среднесписочное число работников составляет 140 чел., объем товарооборота будет находиться в пределах от 1,605 до 1,838 млн.руб. и вероятностью 95% не выйдет за эти пределы.
Пример 2.
По 20 предприятиям региона изучается зависимость выработки продукции на одного работника у(тыс.руб.) от ввода в действие новых основных фондов х1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х2 (%). Данные приведены в таблице.
| № предприятия | Y | X1 | X2 |
| 3,9 | |||
| 3,9 | |||
| 3,7 | |||
| 3,8 | |||
| 4,8 | |||
| 5,4 | |||
| 4,4 | |||
| 5,3 | |||
| 6,8 | |||
| 6,4 | |||
| 6,8 | |||
| 7,2 | |||
| 8,2 | |||
| 8,1 | |||
| 8,5 | |||
| 9,6 | |||
1. Написать уравнение множественной регрессии. Оценить значимость его параметров. Пояснить экономический смысл.
2. Определить коэффициент детерминации с помощью F-критерия Фишера. Оценить статистическую надежность уравнения регрессии.
3. Проанализировать линейные коэффициенты парной и частной корреляции.
4. С помощью частных F-критерия Фишера оценить целесообразность включения в уравнение множественной регрессии фактора х2 после х1.
Решение
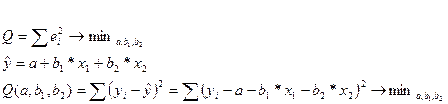
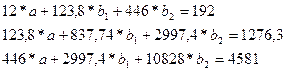
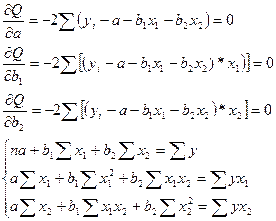
Система из трех нормальных уравнений содержит три неизвестные. Решаем ее и получаем вектор оценок параметров в регрессии [a,b1,b2].
| a= 1,83530694 | |
| b1=0,94594772 | |
| b2=0,08561779 Оценённое уравнение регресии |
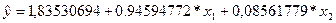
Определим квадрат коэффициента множественной корреляции (коэффициент детерминации), который характеризует долю вариации зависимой переменной, объясненной с помощью данного уравнения.

Включенные в регрессию факторы объясняют 94.69% вариации у. Вариация выработки продукции на одного работника на 94.69% определяется вводом в действие новых основных фондов и удельным весом рабочих высокой квалификации.
Определим коэффициент множественной корреляции.
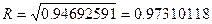 означает тесную связь выработки продукции на одного работника с учтенными в модели факторами.
означает тесную связь выработки продукции на одного работника с учтенными в модели факторами.
Определим тесноту связи между вводом в действие новых основных фондов и выработкой продукции на одного работника, между удельным весом рабочих высокой квалификации и выработкой продукции на одного работника, а также между вводом в действие новых основных фондов и удельным весом рабочих высокой квалификации.
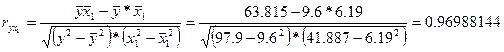
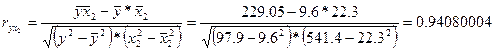
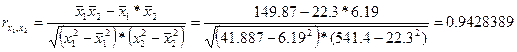
Коэффициенты b1 и b2 нельзя интерпретировать как показатели раздельного влияния х1 и х2 на у, так как между ними существует тесная корреляционная связь.
Статистическую значимость уравнения регрессии оцениваем через
F-критерия Фишера.
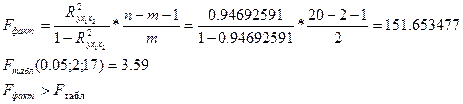
Уравнение регрессии в целом статистически значимо.
Определим частные коэффициенты корреляции. Частные коэффициенты корреляции позволяют выполнить ранжировку факторов по силе их воздействия на результат.
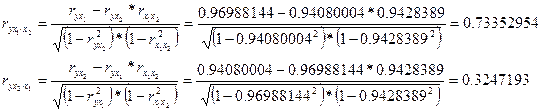
Ввод в действие новых основных фондов оказывает более сильное влияние на выработку продукции на одного работника, чем удельный вес рабочих высокой квалификации.
Проверим целесообразность включения в модель фактора х2 после включенного ранее фактора х1.
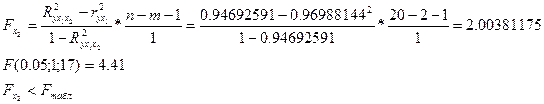
Т.к. 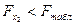 , то включение х2 после х1 нецелесообразно, т.е. влияние удельного веса рабочих высокой квалификации не является устойчивым. Можно ограничиться построением линейного уравнения парной регрессии у(х1).
, то включение х2 после х1 нецелесообразно, т.е. влияние удельного веса рабочих высокой квалификации не является устойчивым. Можно ограничиться построением линейного уравнения парной регрессии у(х1).
Для определения статистической значимости коэффициентов регрессии в целом используется распределение Стьюдента. Проверяется нулевая гипотеза о равенстве tb2=0, т.е. нет регрессионной зависимости. Если расчетное значение t по модулю не превосходит табличного значения, то принимается нулевая гипотеза об отсутствии значимой зависимости, в противном случае нулевую гипотезу отклоняем.
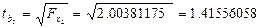
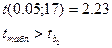
Статистическая значимость коэффициента регрессии 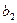 при х2 не подтверждается, т.е.
при х2 не подтверждается, т.е. 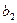 сформировался под влиянием случайных явлений, его можно исключить как неинформативный.
сформировался под влиянием случайных явлений, его можно исключить как неинформативный.
Гипотезу о несущественности коэффициента принимаем.
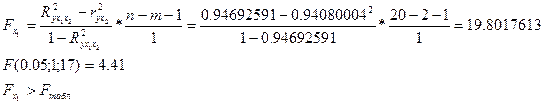
Включение в модель фактора х1 статистически оправдано.
Проверяется нулевая гипотеза о равенстве tв1=0, т.е. нет регрессионной зависимости. Если расчетное значение t по модулю не превосходит табличного значения, то принимается нулевая гипотеза об отсутствии значимой зависимости, в противном случае нулевую гипотезу отклоняем.
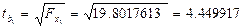
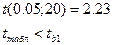
Статистическая значимость коэффициента регрессии 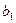 при х1 подтверждается.
при х1 подтверждается.
Определение линейного уравнения парной регрессии.
а=1.98839228
b=1.22966199
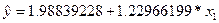
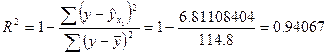
Включенные в регрессию фактор ввод в действие новых основных фондов объясняет 94.69% вариации выработки продукции на одного работника. Статистическую значимость уравнения регрессии оцениваем с помощью F-критерия Фишера.
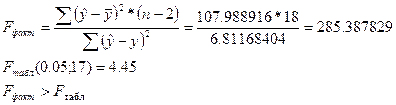
Уравнение регрессии в целом статистически значимо.
Заключение.
Изучены факторы, формирующие значение показателя выработки продукции на одного работника. Первоначально были отобраны два факторных признака: ввод в действие новых основных фондов и удельный вес рабочих высокой квалификации в общей численности рабочих. Получено уравнение множественной регрессии. Качество модели признано хорошим. Установлено, что факторные признаки находятся в тесной линейной корреляционной взаимосвязи, дублируют друг друга , один из них следует исключить из модели. Выполнена ранжировка факторов на основе анализа коэффициентов частной корреляции. Ввод в действие новых основных фондов оказывает более сильное влияние на выработку продукции на одного работника, чем удельный вес рабочих высокой квалификации . Доказана статистическая значимость параметра b1 и случайная природа формирования параметра b2. Модель множественной регрессии с факторами х1 и х2 содержит неинформативный фактор х2, следовательно при моделировании можно ограничиться уравнением парной регрессии. Оценено уравнение парной линейной регрессии ввода в действие новых основных фондов на выработку продукции на одного работника. Распечатка выполненных расчетов прилагается.
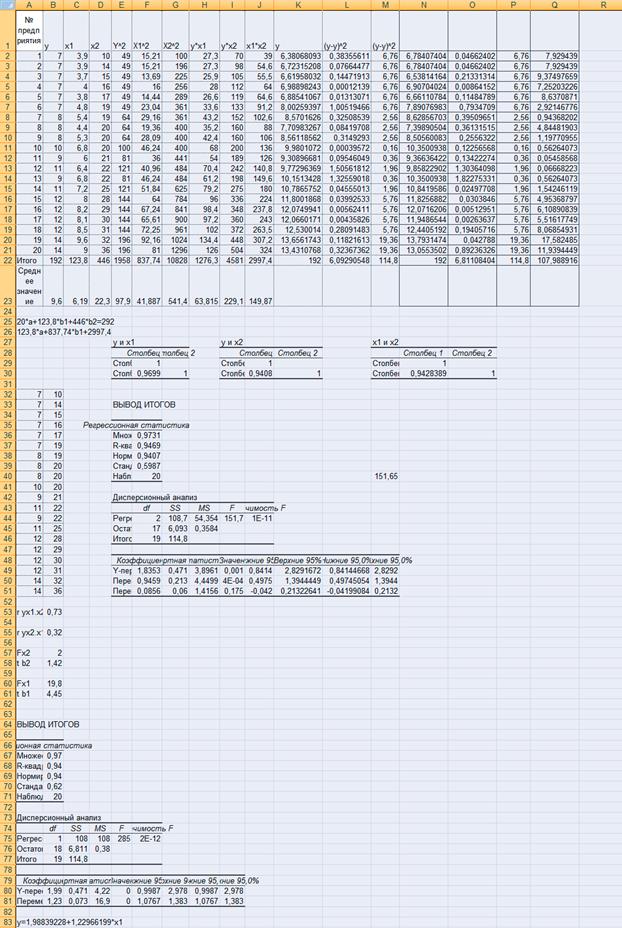
Варианты заданий для контрольных работ.
Тема : Парная регрессия.
Вариант 1.
Данные опроса 8 семей о расходах на продукты питания в зависимости от уровня доходов семьи приведены в таблице (числа относительные ).
| Номер эксперимента | Доходы семьи (Х) | Расходы на продукты питания (Y) |
| 1,4 | 1,1 | |
| 3,3 | 1,4 | |
| 5,5 | ||
| 7,6 | 2,4 | |
| 9,8 | 2,8 | |
| 3,1 | ||
| 14,7 | 3,5 | |
| 18,9 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Оцените тесноту связи.
3. Рассчитайте параметры парной линейной регрессии.
4. Оцените значимость уравнения регрессии с помощью коэффициента детерминации.
5. Оцените силу связи фактора с результатом.
6. С помощью F – критерия Фишера определите статистическую надежность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозируется увеличение значения фактора на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Выводы оформите в аналитической записке.
Вариант 2.
По 17 регионам страны изучается зависимость ежемесячного среднедушевого дохода Y ( тыс.руб) от удельного веса населения в трудоспособном возрасте в общей численности населения, Х (%).
| № региона | Х | Y |
| 60,6 | 3,4 | |
| 59,6 | 3,1 | |
| 60.8 | 3,7 | |
| 59,4 | 3,4 | |
| 60,4 | 3,6 | |
| 60,8 | 3,3 | |
| 60,6 | 3,1 | |
| 59,3 | 3,3 | |
| 60,3 | 3,6 | |
| 62,3 | 4,7 | |
| 3,3 | ||
| 61,4 | 4,1 | |
| 58,9 | 3,4 | |
| 3,2 | ||
| 59,2 | 3,4 | |
| 3,9 | ||
| 60,2 | 3,2 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между факторами.
2. Оцените тесноту связи.
3. Рассчитайте параметры парной линейной регрессии и поясните их смысл.
4. Оцените значимость уравнения регрессии с помощью коэффициента детерминации.
5. Оцените силу связи фактора с результатом.
6. С помощью F – критерия Фишера определите статистическую надежность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозируется увеличение значения фактора на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Выводы оформите в аналитической записке.
Вариант 3.
Имеются данные по 10 хозяйствам.
| № хозяйства | Урожайность, ц/га, У | Внесено удобрений, кг/га, Х |
| 2,1 | ||
| 3,6 | ||
| 3,5 | ||
| 5,0 | ||
| 6,5 | ||
| 4,2 | ||
| 6,3 | ||
| 4,0 | ||
| 6,0 | ||
| 7,5 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между факторами.
2. Оцените тесноту связи.
3. Рассчитайте параметры парной линейной регрессии и поясните их смысл.
4. Оцените значимость уравнения регрессии с помощью коэффициента детерминации.
5. Оцените силу связи фактора с результатом.
6. С помощью F – критерия Фишера определите статистическую надежность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозируется увеличение значения фактора на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Выводы оформите в аналитической записке.
Вариант 4.
По 7 областям региона известны данные о расходах на покупку продовольственных товаров и среднемесячной заработной плате 1 работающего.
| № региона | Расходы на покупку продовольственных товаров, % к общему объему расходов, Y | Среднемесячная заработная плата 1 работающего,тыс.руб., Х |
| 68,8 | 4,5 | |
| 58,3 | 5,9 | |
| 62,6 | 5,7 | |
| 52,1 | 7,2 | |
| 54,5 | 6,2 | |
| 57,1 | ||
| 7,8 | ||
| 47,7 | ||
| 47,1 | 8,1 | |
| 45,5 | 8,4 | |
| 45,4 | 8,5 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между факторами.
2. Оцените тесноту связи.
3. Рассчитайте параметры парной линейной регрессии и поясните их смысл.
4. Оцените значимость уравнения регрессии с помощью коэффициента детерминации.
5. Оцените силу связи фактора с результатом.
6. С помощью F – критерия Фишера определите статистическую надежность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозируется увеличение значения фактора на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Выводы оформите в аналитической записке.
Вариант 5.
Имеются следующие данные о работе строительно-монтажных организаций:
| № организации | Объем выполненных строительно-монтажных работ,млн.руб.,Х | Прибыль,млн.руб.,Y |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между факторами .
2. Оцените тесноту связи.
3. Рассчитайте параметры парной линейной регрессии и поясните их смысл.
4. Оцените значимость уравнения регрессии с помощью коэффициента детерминации.
5. Оцените силу связи фактора с результатом.
6. С помощью F – критерия Фишера определите статистическую надежность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозируется увеличение значения фактора на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Выводы оформите в аналитической записке.
Вариант 6.
По группе промышленных предприятий получены следующие данные:
| № завода | Текучесть кадров, % | Выполнение плана по производительности труда,% |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между факторами .
2. Оцените тесноту связи.
3. Рассчитайте параметры парной линейной регрессии и поясните их смысл.
4. Оцените значимость уравнения регрессии с помощью коэффициента детерминации.
5. Оцените силу связи фактора с результатом.
6. С помощью F – критерия Фишера определите статистическую надежность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозируется увеличение значения фактора на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Выводы оформите в аналитической записке.
Вариант 7.
Имеются данные о стаже работы и месячной выработке продукции рабочих:
| Номер рабочего | Стаж работы, лет | Среднемесячная выработка,тыс. руб |
| 6,5 | ||
| 9,2 | ||
| 4,5 | ||
| 2,5 | ||
| 2,7 | ||
| 13,2 | ||
| 10,5 | ||
| 10,2 | ||
| 5,4 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между факторами .
2. Оцените тесноту связи.
3. Рассчитайте параметры парной линейной регрессии и поясните их смысл.
4. Оцените значимость уравнения регрессии с помощью коэффициента детерминации.
5. Оцените силу связи фактора с результатом.
6. С помощью F – критерия Фишера определите статистическую надежность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозируется увеличение значения фактора на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Выводы оформите в аналитической записке
Вариант 8.
Известны следующие данные по ряду банков:
| № банка | Суммарный актив, млрд.дол. | Объем вложений акционеров, млрд.дол. |
| 507,2 | 19,5 | |
| 506,6 | 19,8 | |
| 487,8 | 21,1 | |
| 18,6 | ||
| 493,6 | 19,6 | |
| 458,9 | 11,7 | |
| 429,3 | 10,5 | |
| 386,9 | 13,6 | |
| 311,5 | 10.8 | |
| 302,2 | 10,9 | |
| 10,3 | ||
| 242,4 | 10,6 | |
| 231,9 | 8,5 | |
| 214,3 | 6,7 | |
| 208,4 | 8,3 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между факторами .
2. Оцените тесноту связи.
3. Рассчитайте параметры парной линейной регрессии и поясните их смысл.
4. Оцените значимость уравнения регрессии с помощью коэффициента детерминации.
5. Оцените силу связи фактора с результатом.
6. С помощью F – критерия Фишера определите статистическую надежность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозируется увеличение значения фактора на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Выводы оформите в аналитической записке.
Вариант 9.
Данные опроса 8 семей о расходах на продукты питания в зависимости от уровня доходов семьи приведены в таблице (числа относительные в расчете на 100 руб. дохода и расхода).
| Номер эксперимента | Доходы семьи (Х) | Расходы на продукты питания (Y) |
| 2,2 | 2,1 | |
| 3,3 | 2,4 | |
| 5,5 | ||
| 7,6 | 3,4 | |
| 9,8 | 3,8 | |
| 4,1 | ||
| 14,7 | 4,5 | |
| 18,9 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между факторами .
2. Оцените тесноту связи.
3. Рассчитайте параметры парной линейной регрессии.
4. Оцените значимость уравнения регрессии с помощью коэффициента детерминации.
5. Оцените силу связи фактора с результатом.
6. С помощью F – критерия Фишера определите статистическую надежность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозируется увеличение значения фактора на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Выводы оформите в аналитической записке.
Вариант 10.
По 17 регионам страны изучается зависимость ежемесячного среднедушевого дохода Y ( тыс.руб) от удельного веса населения в трудоспособном возрасте в общей численности населения, Х (%).
| № региона | Х | Y |
| 60,6 | 3,4 | |
| 59,6 | 3,1 | |
| 60.8 | 3,7 | |
| 59,4 | 3,4 | |
| 60,4 | 3,6 | |
| 60,8 | 3,3 | |
| 60,6 | 3,1 | |
| 59,3 | 3,3 | |
| 60,3 | 3,6 | |
| 62,3 | 4,7 | |
| 3,3 | ||
| 61,4 | 4,1 | |
| 58,9 | 3,4 | |
| 3,2 | ||
| 59,2 | 3,4 | |
| 3,9 | ||
| 60,2 | 3,2 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между факторами .
2. Оцените тесноту связи.
3. Рассчитайте параметры парной линейной регрессии и поясните их смысл.
4. Оцените значимость уравнения регрессии с помощью коэффициента детерминации.
5. Оцените силу связи фактора с результатом.
6. С помощью F – критерия Фишера определите статистическую надежность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозируется увеличение значения фактора на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Выводы оформите в аналитической записке.
Тема : Множественная регрессия.
Вариант 1.
Представлен реальный доход на душу населения Y (ден.ед.), процент рабочей силы, занятой в сельском хозяйстве Х1 и средний уровень образования населения в возрасте после 25 лет Х2 ( число лет, проведенных в учебном заведении) для 15 стран:
| Страна | Y | X1 | X2 |
1. Написать уравнение множественной регрессии. Пояснить смысл параметров.
2. Оценить статистическую надежность уравнения регрессии с помощью коэффициента детерминации и F- критерия Фишера.
3. Проанализировать линейные коэффициенты парной и частной корреляции.
4. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии факторов.
Выводы оформите в аналитической записке.
Вариант 2.
По 20 предприятиям региона изучается зависимость выработки продукции на одного работника Y( тыс.руб.) от ввода в действие новых основных фондов Х1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих Х2 (%).
| № предприятия | Y | X1 | X2 |
| 3,9 | |||
| 3,9 | |||
| 3,7 | |||
| 3,8 | |||
| 4,8 | |||
| 5,4 | |||
| 4,4 | |||
| 5,3 | |||
| 6,8 | |||
| 6,4 | |||
| 6,8 | |||
| 7,2 | |||
| 8,2 | |||
| 8,1 | |||
| 8,5 | |||
| 9,6 | |||
1. Написать уравнение множественной регрессии. Пояснить смысл параметров.
2. Оценить статистическую надежность уравнения регрессии с помощью коэффициента детерминации и F- критерия Фишера.
3. Проанализировать линейные коэффициенты парной и частной корреляции.
4. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии факторов.
Выводы оформите в аналитической записке.
Вариант 3.
По 10 филиалам предприятия известны следующие данные:
| № филиала | Производительность труда (Y) | Фондовооруженность (Х1) | Энерговооруженность (Х2) |
1. Написать уравнение множественной регрессии. Пояснить смысл параметров.
2. Оценить статистическую надежность уравнения регрессии с помощью коэффициента детерминации и F- критерия Фишера.
3. Проанализировать линейные коэффициенты парной и частной корреляции.
4. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии факторов.
Выводы оформите в аналитической записке.
Вариант 4.
Имеются следующие данные о выработке продукции Y (тыс. шт.), среднемесячной заработной плате рабочих Х1 (ден.ед.) и потерях рабочего времени Х2(ч.):
| № рабочего | Y | Х1 | Х2 |
| 8,5 | 15,8 | ||
| 8,0 | 16,0 | ||
| 9,4 | 12,3 | ||
| 12,0 | 2,5 | ||
| 10,5 | 5,4 | ||
| 9,0 | 9,8 | ||
| 9,5 | 7,4 | ||
| 5,4 | 21,0 | ||
| 4,8 | 21,3 | ||
| 9,3 | 5,7 | ||
| 12,6 | 2,8 | ||
| 8,8 | 2-6 | 6,9 | |
| 7,1 | 14,5 | ||
| 6,5 | 17,8 | ||
| 9,0 | 6,5 | ||
| 6,3 | 16,9 |
1. Написать уравнение множественной регрессии. Пояснить смысл параметров.
2. Оценить статистическую надежность уравнения регрессии с помощью коэффициента детерминации и F- критерия Фишера.
3. Проанализировать линейные коэффициенты парной и частной корреляции.
4. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии факторов.
Выводы оформите в аналитической записке.
Вариант 5.
Результаты хозяйственной деятельности торговых предприятий за год приведены в таблице:
| № предприятия | Уровень рентабельности,% | Удельный вес продовольственных товаров в товарообороте,% | Время обращения товаров, дней |
| 3,62 | 74,2 | ||
| 3,8 | 73,5 | ||
| 2,77 | |||
| 2,12 | 84,3 | ||
| 4,33 | 67,3 | ||
| 4,01 | 70,1 | ||
| 2,01 | 83,1 |
1. Написать уравнение множественной регрессии. Пояснить смысл параметров.
2. Оценить статистическую надежность уравнения регрессии с помощью коэффициента детерминации и F- критерия Фишера.
3. Проанализировать линейные коэффициенты парной и частной корреляции.
4. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии факторов.
Выводы оформите в аналитической записке.
Вариант 6.
Данные опроса десяти групп семей о расходах на говядину в зависимости от цены на говядину и на свинину приведены в таблице:
| № семьи | Расходы на говядину | Цена на говядину | Цена на свинину |
1. Написать уравнение множественной регрессии. Пояснить смысл параметров.
2. Оценить статистическую надежность уравнения регрессии с помощью коэффициента детерминации и F- критерия Фишера.
3. Проанализировать линейные коэффициенты парной и частной корреляции.
4. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии факторов.
Выводы оформите в аналитической записке.
Вариант 7.
Результаты обследования десяти статистически однородных строительных организаций приведены в таблице
| Общая сумма затрат | Объем выполненных работ | Число рабочих | |
| 5,9 | |||
| 4,8 | |||
| 4,6 | |||
| 6,1 | |||
| 5,3 | |||
| 5,6 | |||
| 6,6 | |||
| 6,1 | |||
| 6,3 | |||
| 5,1 |
1. Написать уравнение множественной регрессии. Пояснить смысл параметров.
2. Оценить статистическую надежность уравнения регрессии с помощью коэффициента детерминации и F- критерия Фишера.
3. Проанализировать линейные коэффициенты парной и частной корреляции.
4. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии факторов.
Выводы оформите в аналитической записке.
Вариант 8.
Дана зависимость уровня рентабельности торговой деятельности от удельного веса продовольственных товаров и оплаты труда.
| № торгового предприятия | Уд.вес продов. товаров в товарообороте,% | Среднемесячная оплата труда, ден.ед. | Уровень рентабельности,% |
| 74,2 | 3,62 | ||
| 73,5 | 3,8 | ||
| 2,77 | |||
| 84,3 | 2,12 | ||
| 67,3 | 4,33 | ||
| 70,1 | 4,01 | ||
| 83,1 | 2,01 | ||
| 3,05 | |||
| 3,6 |
1. Написать уравнение множественной регрессии. Пояснить смысл параметров.
2. Оценить статистическую надежность уравнения регрессии с помощью коэффициента детерминации и F- критерия Фишера.
3. Проанализировать линейные коэффициенты парной и частной корреляции.
4. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии факторов.
Выводы оформите в аналитической записке.
Вариант 9.
Представлен реальный доход на душу населения Y (ден.ед.), процент рабочей силы, занятой в сельском хозяйстве Х1 и средний уровень образования населения в возрасте после 25 лет Х2 ( число лет, проведенных в учебном заведении) для 15 стран:
| Страна | Y | X1 | X2 |
1. Написать уравнение множественной регрессии. Пояснить смысл параметров.
2. Оценить статистическую надежность уравнения регрессии с помощью коэффициента детерминации и F- критерия Фишера.
3. Проанализировать линейные коэффициенты парной и частной корреляции.
4. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии факторов.
Выводы оформите в аналитической записке.
Вариант 10.
По 10 филиалам предприятия известны следующие данные:
| № филиала | Производительность труда (Y) | Фондовооруженность (Х1) | Энерговооруженность (Х2) |
1. Написать уравнение множественной регрессии. Пояснить смысл параметров.
2. Оценить статистическую надежность уравнения регрессии с помощью коэффициента детерминации и F- критерия Фишера.
3. Проанализировать линейные коэффициенты парной и частной корреляции.
4. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии факторов.
Выводы оформите в аналитической записке.
ТЕМА: ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЯХ .
Построение аддитивной модели временного ряда включает следующие шаги:
1) Выравнивание исходного ряда методом скользящей средней;
2) Расчет значений сезонной компоненты S;
3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (T+Е);
4) Получение уравнения тренда и расчет значений Т с использованием полученного уравнения тренда;
5) Расчет полученных по модели значений (Т+S);
Пример.
В таблице №1 приведены данные по динамике производства яиц в РФ за период 1999-2002 гг.
Динамика производства яиц в России. Табл.1.
| Год | Квартал | Производство, млрд.шт. |
| 7,5 | ||
| 9,1 | ||
| 9,1 | ||
| 7,5 | ||
| 7,8 | ||
| 9,3 | ||
| 9,1 | ||
| 7,7 | ||
| 7,7 | ||
| 9,7 | ||
| 9,7 | ||
| 8,1 | ||
| 8,3 | ||
| 9,8 | ||
| 8,2 |
1. Постройте график временного ряда.
2. Постройте аддитивную модель временного ряда.
3. Оцените качество модели.
4. Дать прогноз производства яиц в первом полугодии ближайшего следующего (5-го) года.
Построение аддитивной модели.
1. Выравнивание исходного ряда методом скользящей средней. Расчет оценок сезонной компоненты в аддитивной модели.
| Год | Квартал | t | 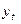 млрд шт млрд шт
| Итого за 4 квартала | Скользящая средняя за 4 квартала | Центрированная скользящая средняя | Оценка сезонной компоненты |
| 7,5 | |||||||
| 9,1 | |||||||
| 9,1 | 33,2 | 8,3000 | 8,3375 | 0,7625 | |||
| 7,5 | 33,5 | 8,3750 | 8,4000 | -0,9000 | |||
| 7,8 | 33,7 | 8,4250 | 8,4250 | -0,6250 | |||
| 9,3 | 33,7 | 8,4250 | 8,4500 | 0,8500 | |||
| 9,1 | 33,9 | 8,4750 | 8,4625 | 0,6375 | |||
| 7,7 | 33,8 | 8,4500 | 8,5000 | -0,8000 | |||
| 7,7 | 34,2 | 8,5500 | 8,6250 | -0,9250 | |||
| 9,7 | 34,8 | 8,7000 | 8,7500 | 0,9500 | |||
| 9,7 | 35,2 | 8,8000 | 8,8750 | 0,8250 | |||
| 8,1 | 35,8 | 8,9500 | 8,9875 | -0,8875 | |||
| 8,3 | 36,1 | 9,0250 | 9,0375 | -0,7375 | |||
| 36,2 | 9,0500 | 9,0625 | 0,9375 | ||||
| 9,8 | 36,3 | 9,0750 | |||||
| 8,2 |
2. Расчет значений сезонной компоненты в аддитивной модели.
Найдем оценки сезонной компоненты по следующей формуле
[фактическое уравнение ряда]-[центрированная скользящая средняя]
| Показатель | Год | Номер квартала | |||
| - | - | 0,7625 | -0,9000 | ||
| -0,6250 | 0,8500 | 0,6375 | -0,8000 | ||
| -0,9250 | 0,9500 | 0,8250 | -0,8875 | ||
| -0,7375 | 0,9375 | - | - | ||
| Итого за i квартал | -2,2875 | 2,7375 | 2,2250 | -2,5875 | |
Средняя оценка сезонной компоненты для i квартала 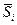
| -0,7625 | 0,9125 | 0,7417 | -0,8625 | |
Скорректированная сезонная компонента 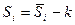
| -0,7698 | 0,9052 | 0,7344 | -0,8698 |
В моделях с сезонной компонентой предполагается, что сезонные воздействия взаимно погашаются.
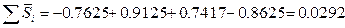
Рассчитаем корректирующий коэффициент.

Скорректированные значения сезонной компоненты найдем по формуле
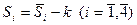
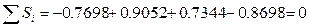
3. Устранение сезонной компоненты из исходных данных уровня ряда и получение выровненных данных 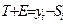 . Данные приведены в таблице.
. Данные приведены в таблице.
| Год | Квартал | t | 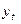 , млрд шт , млрд шт
| Скорректированная сезонная компонента 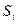
| 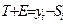
|
| 7,5 | -0,7698 | 8,2698 | |||
| 9,1 | 0,9052 | 8,1948 | |||
| 9,1 | 0,7344 | 8,3656 | |||
| 7,5 | -0,8698 | 8,3698 | |||
| 7,8 | -0,7698 | 8,5698 | |||
| 9,3 | 0,9052 | 8,3948 | |||
| 9,1 | 0,7344 | 8,3656 | |||
|
Дата добавления: 2014-12-08; просмотров: 3386; |
Генерация страницы за: 0.288 сек.
