Интегралдық есептеулер

Любиш експериментувати, подобаються оригінальні ідеї, з задоволенням створюєш із простих буденних речей справжні витвори мистецтва? Тоді, думаю, цей урок буде Тобі до душі. Пропоную разом зі мною створити ажурні незвичні ялинкові прикраси із… макаронних виробів.)
1 3 609 0
Для роботи Тобі потрібні:
1. макаронні вироби різних форм, але особливо ефектні фігурні округлі або ж у формі черепашок;
2. термопістолет для клею;
3. підкладка для візерункової композиції, найкраще підійде пластикова;
4. фарби: біла, золота, срібляста, гарно виглядатиме сніжинка блакитна або червона;
5. блискітки: сухі або у тюбику;
6. стрічка, нитка, тасьма — те, на чому висітиме сніжинка.
До роботи!

Висипаємо на спеціально відведене для цього місце макаронні вироби різних форм. Звісно, спочатку запитай дозволу у мами, а ще краще якщо вона сама виділить необхідну кількість їстівних «детальок». Спочатку без клею, просто складаємо із них цікаві візерунки. Ось тут Ти можеш проявити свою безмежну фантазію, аби створити оригінальну, не схожу на усі інші, казкову прикрасу.

Як тільки вийде гарна сніжинка, наносимо крапельками термо-клей у тих місцях, де макаронинки стикаються між собою. Коли клей засохне, можна починати прикрашати сніжинку: розфарбовувати, посипати блискітками, оздоблювати бісером. Ефект та остаточний результат залежатиме тільки від Твого старання та власних ідей.


Непогана прикраса вийде і з продовгуватих макаронів.

Уважно вивчи весь процес роботи, а потім і сам приступай до створення оригінальної ялинкової прикраси. Здивування та захват родичів і знайомих гарантовані.




Удачі!
ДДД
 дқ
дқ  нжо:
нжо:  теңсіздігін қанағаттандыратын барлық нүктелер үшін жинақсыз
теңсіздігін қанағаттандыратын барлық нүктелер үшін жинақсыз
 дқ
дқ  нжо:
нжо:  шартын қанағаттандыратын барлық z нүктелер үшін абсолютті жинақты
шартын қанағаттандыратын барлық z нүктелер үшін абсолютті жинақты
дқжрДбқт: 
дқжрКбқт: 
Е 
 dz : -1
dz : -1
Е  ж
ж  б,о
б,о  А)
А) 
Е  = А)
= А) 
Е  б,о
б,о  А)
А) 
Е  dz, Г:Іz-πІ=1 : 0
dz, Г:Іz-πІ=1 : 0
Е F(p)=  -дбб, B(p)бт
-дбб, B(p)бт  сайкес
сайкес  еб,о F(p)-нт: f(t)=
еб,о F(p)-нт: f(t)= 
Е F(p)=  -дрбб,B(p) бтқж
-дрбб,B(p) бтқж  тб,оF(p)-н т: f(t)=
тб,оF(p)-н т: f(t)= 
Е(t)÷F(p)б,о  :
: 
Е(t)÷F(p)б,о  :
: 
 фбт:
фбт: 
Е  ,
,  б,о
б,о  :
: 
ЕЕЕ
Е𝑓(t)  жТпб,ооб >
жТпб,ооб > 
 : s w:val="16"/><w:lang w:val="KZ"/></w:rPr><m:t>-pt</m:t></m:r></m:sup></m:sSup></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
: s w:val="16"/><w:lang w:val="KZ"/></w:rPr><m:t>-pt</m:t></m:r></m:sup></m:sSup></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 
Е𝑓(t)÷F(p) б,о  ү
ү  :
: 
Е𝑓(t)÷F(p) б,отиб  :
: 
Е𝑓(t)÷F(p) бо  :
: 
Е𝑓(t)  б,о𝑓(
б,о𝑓(  t)
t)  :
: 
енеенде:  ЖЖЖ
ЖЖЖ
жДб: 
ЖДбк:  , l≤1
, l≤1
Женде: 
енпде: 
жКб: 
ЖКибк: 
ка  сқжбо:
сқжбо: 
Каf(x)фLқбиқфе:  Касққөа:
Касққөа:  кафқк:
кафқк:  кж
кж  қ жинақсыз е:
қ жинақсыз е: 
кж  сқ жинақты е:
сқ жинақты е:  К-Ршққа:
К-Ршққа: 
ККК
Кққд? : 1≑ 
Кс n-ші дт : Wк=  𝒛 = -i ксктж: 1
𝒛 = -i ксктж: 1 
Ксnдшф: 
Ксмее: z=4-3i: 5
қефк:  ЛЛЛ
ЛЛЛ
 қжз: Абсолютті жинақты
қжз: Абсолютті жинақты
 қжз: жинақсыз
қжз: жинақсыз
 қжр: R=1
қжр: R=1
 қжр: R=1
қжр: R=1
 қжр: R=1
қжр: R=1
 қжр:R=
қжр:R=  12
12
 қжр:R=2
қжр:R=2
ҚҚҚ
Лқббк: 
Лқдбқт: 
r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">  мтаққө :
мтаққө :  -шеңбер
-шеңбер
Мф:  n =
n = 
Н-Лфк: 
ННН
Оқә y(0)=0,  (0)=0 бшб
(0)=0 бшб  =2 тш
=2 тш  y(t)=
y(t)= 
Оқә y(0)=0,  (0)=0 бшб
(0)=0 бшб  =t тш
=t тш  y(t)=
y(t)= 
ООО
Р-М фқта: f(t)=  dp
dp
РРР
 тб,ок
тб,ок  А)
А) 
 фб:
фб: 
 фТқжк:
фТқжк: 
 (1+sinz)dz иек,мLқ0(0,0)жА(π,0)нқккк : π+2
(1+sinz)dz иек,мLқ0(0,0)жА(π,0)нқккк : π+2
Эфк: 
ЭЭЭ
𝑓(t) =  жf'(0)=
жf'(0)=  ,о : 𝑓′′
,о : 𝑓′′ 
F

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|


|
Интегралдық есептеулер
$$$ 1.
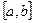 кесіндісіндегі
кесіндісіндегі 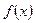 функциясының анықталған интегралы
функциясының анықталған интегралы 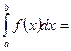
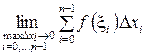
$$$ 2.
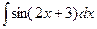 анықталмаған интегралын есептеңіз:
анықталмаған интегралын есептеңіз:
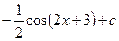
$$$ 3.
Егер 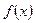 функциясы жұп болса, онда
функциясы жұп болса, онда 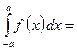
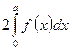
$$$ 4.
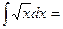
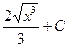
$$$ 5.
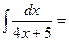
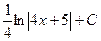
$$$ 6.
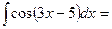
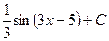
$$$ 7
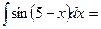
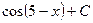
$$$ 8
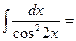
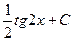
$$$ 9
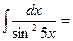
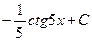
$$$ 10
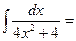
A) 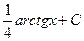
$$$ 11
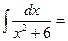
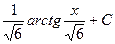
$$$ 12
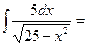
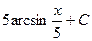
$$$ 13
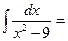
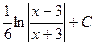
$$$ 14
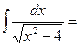
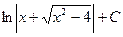
$$$ 15
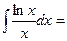
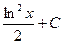
$$$ 16
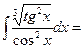
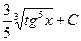
$$$ 17
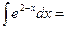
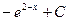
$$$ 18
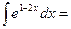
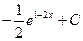
$$$ 19
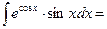
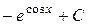
$$$ 20
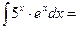
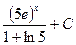
$$$ 21
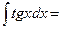
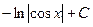
$$$ 22
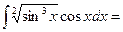
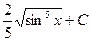
$$$ 23
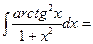
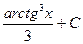
$$$ 24
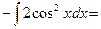
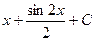
$$$ 25
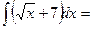
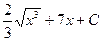
$$$ 26
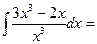
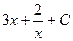
$$$ 27
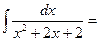
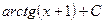
$$$ 28
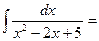
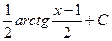
$$$ 29
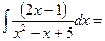
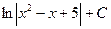
$$$ 30
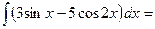
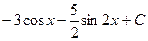
$$$ 31
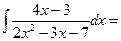
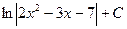
$$$ 32
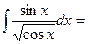
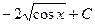
$$$ 33
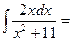
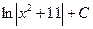
$$$ 34
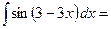
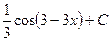
$$$ 35
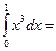
1/4
$$$ 36
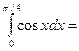
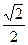
$$$ 37
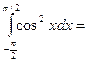
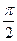
$$$ 38
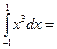
$$$ 39
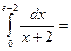
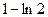
$$$ 40
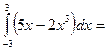
$$$ 41
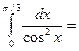
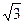
$$$ 42
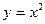 ,
, 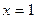 ,
, 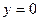 сызықтарымен қоршалған жазық фигураның ауданын есептеу керек
сызықтарымен қоршалған жазық фигураның ауданын есептеу керек
1/3
$$$ 43
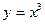 ,
, 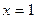 ,
, 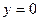 сызықтарымен қоршалған жазық фигураның ауданын есептеу керек
сызықтарымен қоршалған жазық фигураның ауданын есептеу керек
1/4
$$$ 44
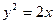 ,
, 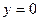 ,
, 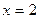 сызықтарымен қоршалған жазық фигураның ауданын есептеу керек
сызықтарымен қоршалған жазық фигураның ауданын есептеу керек
8/3
$$$ 45
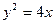 ,
, 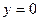 ,
, 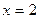 сызықтарымен қоршалған жазық фигураның ауданын есептеу керек
сызықтарымен қоршалған жазық фигураның ауданын есептеу керек
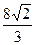
$$$ 46
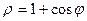 сызығымен қоршалған жазық фигураның ауданын есептеу керек
сызығымен қоршалған жазық фигураның ауданын есептеу керек
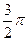
$$$ 47
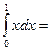
1/2
$$$ 48
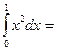
1/3
$$$ 49
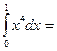
1/5
$$$ 50
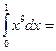
1/10
$$$ 51
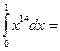
1/15
$$$ 52
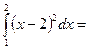
1/3
$$$ 53
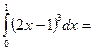
$$$ 54
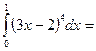
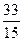
$$$ 55
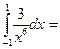
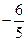
$$$ 56
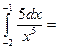
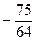
$$$ 57
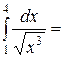
$$$ 58
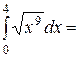
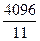
$$$ 59
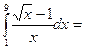
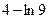
$$$ 60
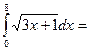
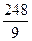
$$$ 61
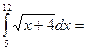
74/3
$$$ 62
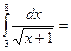
$$$ 63
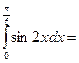
1/4
$$$ 64
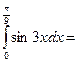
1/6
$$$ 65
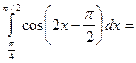
1/2
$$$ 66
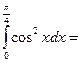
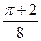
$$$ 67
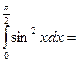
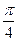
$$$ 68
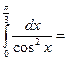
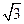
$$$ 69
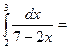
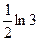
$$$ 70
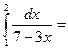
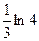
$$$ 71
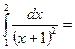
1/6
Дата добавления: 2014-12-06; просмотров: 1315;
