Критерій граничного рівня

Критерій граничного рівня не дає оптимального рішення, наприклад, максимуму прибутку або мінімуму витрат. За цим критерієм можна визначити допустимий спосіб дій.

Припустимо, що величина попиту х за одиницю часу (інтенсивність попиту) на деякий товар задається неперервною функцією розподілу f(x). Якщо запаси в початковий момент невеликі і в подальшому можливий дефіцит товару. У протилежному випадку до кінця розглянутого періоду запаси нереалізованого товару можуть виявитись дуже великими. В обох випадках втрати не оминемо. У першому випадку зменшується потенційний прибуток і передбачається втрата клієнтів, у другому – збільшуються витрати відповідно на доставку та зберігання товару.

Можливий компроміс полягає у виборі рішення, яке балансує два види вказаних втрат. Оскільки визначити втрати від дефіциту дуже важко, особа, яка приймає рішення, може встановити необхідний рівень запасів таким чином, щоб величина очікуваного дефіциту не перевищувала А₁ одиниць, а величина очікуваних надлишків не перевищувала А₂ одиниці. Виразимо математично ці умови. Нехай R – граничний рівень запасів. Тоді очікуваний дефіцит

, (12.10)

а очікуваний надлишок

. (12.11)

При довільному виборі А₁ і А₂ вказані умови можуть виявитися суперечливими. В цьому випадку для забезпечення допустимості розв’язку необхідно послабити одне з обмежень.

Приклад 12.3. Величина попиту х на деякий товар задається функцією розподілу, щільність якої має вигляд:

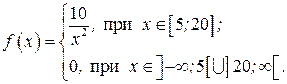
Знайти граничний рівень запасу R.

¨Розв’язування.

Перейдемо до визначення очікуваного дефіциту:

.

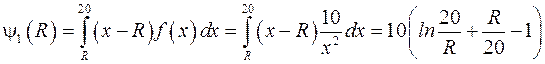Аналогічно знайдемо очікуваний надлишок:

.

Використання критерію граничного рівня приведе до таких нерівностей:

Виконаємо відповідні перетворення:

Остаточно маємо:

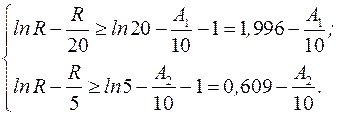
Граничні значення А₁ і А₂ повинні бути вибрані так, щоб обидві нерівності виконувались принаймні для одного значення R. Наприклад, покладемо А₁ =2 і А₂= 5. Тоді нерівності набудуть вигляду:

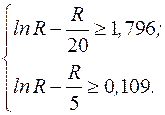
Значення R повинно знаходитись між 5 і 20, тому що в цих границях змінюється попит.

Для визначення множини значеньR побудуємо табл. 12.3, яка показує, що обидві умови виконуються для .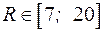

Таблиця 12.3

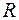
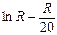
	1,58	1,70	1,85	1,98	2,09	2,19	2,28	2,36	2,44	2,51	2,57	2,63	2,69	2,75	2,80	2,85
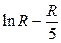
	1,29	1,43	1,56	1,66	1,76	1,84	1,92	1,99	2,05	2,11	2,17	2,22	2,27	2,31	2,36	2,4

12.4. Кількісний аналіз прийняття рішень методом ”дерева цілей”

У попередніх параграфах розглянуто критерії, що дають можливість проводити аналіз вибору з множини одноетапних альтернатив. Тобто господарське рішення, прийняте на перспективу, не залежало від рішень, прийнятих у поточному моменті. В той же час у практичній діяльності виробничих та інших структур досить часто трапляються випадки аналізу багатоетапних процесів прийняття рішень, у яких взаємозалежні управлінські рішення приймаються послідовно. Такий тип рішень піддається графічному моделюванню з допомогою «дерева цілей» (рішень).

Припустимо, що ми сформулювали постановку задачі прийняття інвестиційних рішень, крім того, відомі можливі альтернативи дій, а також визначено ймовірності їх відбуття та корисності наслідків. Інвестор, як особа, котра приймає рішення (ОПР), має можливість вибору альтернатив, але поки що не вирішив, як діяти у цій ситуації. Провівши високоякісний аналіз інвестиційної діяльності, ОПР будує "дерево рішень". Основними його елементами є вершини двох типів: рішення (позначають квадратами – ‚) і випадки (позначають кругом – О). У першому типі вершини вибір повністю визначає ОПР, а в другому – вибір залежить від випадку, тобто не перебуває під наглядом ОПР. В останньому випадку найбільше, що може зробити інвестор, – поставити ймовірності для тих віток дерева, які мають початок у випадкових вершинах. На рис. 12.4.1 вершини 1, 4, 5, 6 є першого типу, а 2, 3, 7, 8 – другого.

Наступний крок дії ОПР полягає у встановленні числових значень наслідків, пов'язаних із раціоналізацією шляхів на "дереві рішень". Розглянемо шлях від початку до деякої умовної точки С. У прикладних дослідженнях із згаданим шляхом будуть пов'язані конкретні затрати, тобто своєрідні наслідки, відбуття яких пов'язане з деякою ймовірністю. Припустимо, що ОПР необхідно здійснити вибір альтернативи або 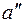, тобто між подіями l₁ або l₂, тоді наслідкам необхідно поставити у відповідність значення величин корисності 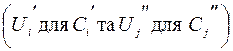так, щоб мало місце співвідношення. Якщо , то справедлива нерівність

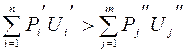, (12.12)

де i та j – індекси станів ; 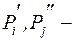відповідні ймовірності, – значення величини корисності відповідно в станах i та j.

Рис. 12.4.1. Основні елементи “дерева цілей”

Це означає, що оптимальною буде та альтернатива, для якої очікувана корисність буде максимальною.

Тоді, починаючи рухатися справа наліво, тобто рух відбувається по дереву в зворотному напрямку, і користуючись раніше встановленим принципом оптимальності (максимум або мінімум), для кожного вузла обчислюють розподіл імовірностей та очікувану корисність. Далі знову для кожного вузла ОПР вибирає таку альтернативу, яка приводить до найбільш очікуваної корисності, і приписуємо отриману корисність вузлу рішень.

Розглянемо аналіз інвестиційної ситуації на умовному прикладі щодо інвестування у випуск певного виду продукції. Інвестор інвестує кошти у випуск продукції П₀, на яку в цей час існує ринковий попит. Наявне технологічне устаткування, фінансовий стан підприємства, існуюча організація праці, маркетингова діяльність дають інвестору стабільний дохід. Разом з тим, інвестор може вкласти інвестиції у випуск продукції підвищеного класу П₁та високого П₂. Попередній фінансовий аналіз показує, що інвестування у випуск продукції П₁ забезпечить інвестору річний приріст прибутку розміром 30 млн. грн. за умови існування на неї ринкового попиту, у протилежному випадку – знизить на 3 млн. грн.

Перехід на випуск продукції П₂ дозволить, у випадку існування попиту, отримати приріст прибутку 50 млн. грн., а за його відсутності інвестор понесе додаткові річні видатки розміром 10 млн. грн.

Імовірність того, що при переході на випуск продукції нового виду, виробник успішно справиться з поставленим завданням, становить 0,8.

Для визначення ринкового попиту інвестор може провести відповідні маркетингові дослідження (експерименти), які призведуть до додаткових витрат розміром 5 млн. грн. Разом із тим, невідомо, як можуть закінчитися проведені дослідження. З досвіду попередніх років інвестор знає, що позитивні висновки справджуються на 70 %, а негативні – на 90 %. Інвестору необхідно прийняти рішення щодо інвестування у випуск нового виду продукції, а якщо переходити, то на П₁, чи на П₂? Крім того, потрібно вирішити питання щодо замовлення дослідження.

Для знаходження оптимального рішення поставленої проблеми можна використати метод "дерево рішень". На практиці згадані виробничі процеси розвиваються в динаміці, тому на першому етапі необхідно встановити їх часову послідовність. Інвесторові необхідно, насамперед, вирішити питання щодо аналізу прогнозної інформації про ринок збуту, тобто замовляти дослідження чи ні. Зрозуміло, що висновки з проведеного дослідження прискорять прийняття більш об'єктивного рішення.

Припустимо, що інвестор вирішив замовити дослідження на прогнозну оцінку ринку збуту. Ця процедура вимагатиме певного часу, доки інвестор отримає висновки з проведеного дослідження. Зміст висновку може передбачити один із двох варіантів: успіх або невдача.

Побудуємо логічну схему процедури прийняття рішень у вигляді "дерева цілей" (рис. 12.4.2). На «дереві» добре видно події, з яких складається процедура прийняття рішень. Буквами А, В, С, Д позначимо стани: А – початковий стан, F₁,…,F₁₅ – кінцевий стан, В, С, Д – стани чи точки розгалуження.

Лінія, що йде від початкової події до будь-якої кінцевої, називається повним шляхом (АВ₀С₀Д₁–повний шлях). Відрізок між двома подіями назвемо віткою (С₁Д₅ – вітка). Як бачимо, процедура прийняття рішень включає події трьох видів: події, що залежать від рішення інвестора (замовлення дослідження, вибір продукції) – це дії; події, що є наслідками рішень інвестора, але на характер яких він не може вплинути; події, коли інвестор не може вплинути на результати висновків замовленого дослідження, назвемо просто подіями.

Із події А виходять дві вітки (дії): l₀ – інвестор не робить замовлення на дослідження та l_і – замовляє дослідження. Вони є змінними процесу прийняття рішень і складають множину . Із стану В₁ виходять дві вітки, які означають такі події: Q₁– дослідження передбачає успіх і Q₂– передбачає невдачу. Зі стану В₀ виходить вітка, яка має лише формальне значення, Q₀(фіктивна подія). На ці події інвестор вплинути не може. Позначимо окреслену сукупність подій як множину .

Із станів С₀, С₁ і С₂ виходять по три вітки, які відображають події: Z₀ – випуск продукції П₀ триває; Z₁ – перехід інвестування на випуск продукції П₁; Z₂ – перехід інвестування на випуск продукції П₂. Вони є змінними процесу прийняття рішень і об'єднуються в множину . Продовжуючи аналіз станів, бачимо, що з Д₂, Д₃, Д₅, Д₆, Д₈, Д₉ виходять по дві вітки, які позначають події: S₁, S₂, відповідно, успіх і невдачу інвестора при переході на інвестування випуску нового виду продукції. На завершення маємо, що із станів Д₁, Д₄, Д₇виходить тільки по одній формальній вітці (S₀),що свідчить про відсутність альтернатив відносно успіху або невдачі випуску П₀.

Згадані вище події не є змінними процесу прийняття рішень, їх множину позначимо через .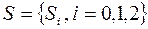

Доповнимо "дерево цілей" числовими даними зміни річного обсягу прибутку. Відповідно до умови задачі прибуток зміниться таким чином: 0 – виробництво продукції П₀ зберігається; +30 – виробництво продукції П₁ за наявності успіху; -3 – виробництво продукції П₁ за відсутності успіху; +50 – виробництво продукції П₂ за наявності успіху; -10 – виробництво продукції П₂ за відсутності успіху.

Помістимо зазначені величини на відповідних логічних гілках ”дерева рішень”. Враховуючи затрати, пов'язані із дослідженням ринку збуту, знайдемо для кожного кінцевого стану величину ефекту (корисності) U_tjki, які відобразимо на кінцях відповідних віток (рис. 12.4.2). Аналізуючи числові результати, бачимо, наскільки більше зв'язаний з ризиком перехід на випуск продукції П₂ порівняно з П₁. Проте окреслений ризик може бути виправданий прогнозною величиною річного прибутку.

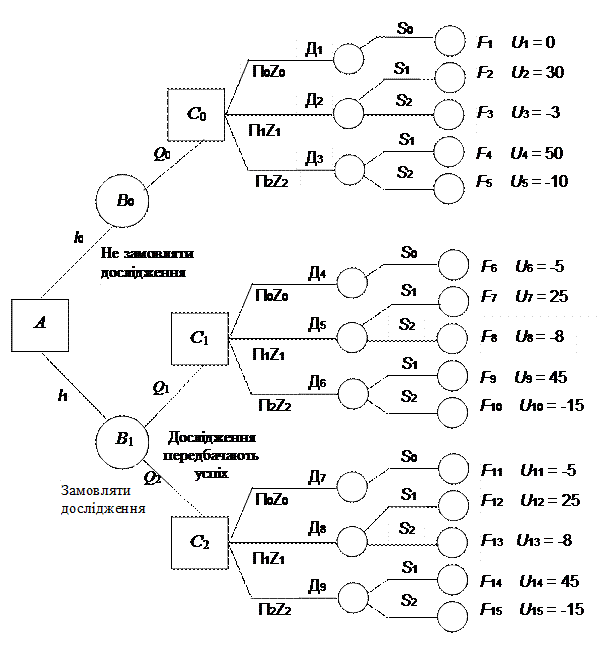
Рис. 12.4.2. Прийняття рішень із допомогою «дерева цілей»

Для отримання ефективного інвестиційного рішення використаємо кількісні значення імовірнісних величин. Припустимо, що інвестор приймає рішення не замовляти дослідження про ринок попиту. Це означає, що ми перебуваємо у вершині рішень С₀ і перед ним стоїть завдання вибору однієї з трьох альтернатив: Z₀, Z₁, Z₂, які означають відповідно випуск продукції П₀, П₁, П₂.

Нехай інвестор вибирає альтернативу Z₀ (точка Д₁), імовірність того, що інвестор не отримає прибутку (U₁= 0), становитиме Р₀ = 1. Якщо інвестор зупиниться на випуску П₁, тоді з вершини Д₂ (вершина випадків) можливий як успіх (S₁) із імовірністю Р(S₁) = 0,8, і в результаті інвестор отримає додатковий прибуток U₂ = 30 млн. грн., так і невдача (S₂) з імовірністю Р(S₂)=0,2 та розміром річних витрат у сумі U₃ = 3 млн. грн. P(S₁) та P(S₂) є суб'єктивними ймовірностями.

Розглянемо аналіз випадку, пов'язаного із випуском продукції П₂. Маємо, що із вершини випадку Д₃, знову виходять дві вітки, які відповідно моделюють успіх (S₁) і невдачу (S₂). Імовірність першого випадку становить 0,8, а другого 0,2 і, як результат, річний прибуток збільшиться відповідно на U₁ = 50 млн. грн. або зменшиться на U₃ = 10 млн. грн.

Перейдемо до аналізу ситуації, пов'язаної із замовленням дослідження на вивчення ринкового попиту. Тоді у вершині випадків В₁ має місце два наслідки, як позитивний Q₁ (дослідження передбачає успіх) із імовірністю Р₁ = 0,7, так і негативний Q₂ (передбачає невдачу) з імовірністю Р₂ = 0,3.

Отримавши висновки замовленого дослідження інвестор, перебуваючи у вершинах випадків С₁ або С₂ повинен знову прийняти рішення щодо вибору однієї з альтернатив {Z_0,, Z₁, Z₂}. Припустимо, що висновок дослідження є позитивним. Продовжуючи випуск продукції П₀, інвестор несе річні видатки розміром U₆= 5 млн. грн. (Р₀ = 1). Вибравши П₁, можна отримати прибуток U₇ =30 – 5 = 25 млн. грн. із імовірністю або витрати U₈=30+5 = 8 млн. грн. з імовірністю 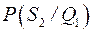. Для випуску продукції П₂ одержимо величину прибутку U₉ = 50 – 5 = 45 млн. грн. або витрат U₁₀ =10 + 5 = =15млн. грн.

Аналогічно проаналізуємо випадок отримання негативного висновку з проведеного дослідження. У вершині С₂ знову можливі три альтернативи {Z₀, Z₁, Z₂}. Прийняття їх дає прибуток U₁₂, U₁₄ або витрати U₁₁ ,U₁₃,U₁₅. Провівши відповідні розрахунки, одержимо:

U₁₁ = 5; U₁₂ = 25; U₁₃= 8;U₁₄= 45;U₁₅ =15 млн. грн.

Розраховані значення будуть характеризуватися ймовірностями 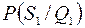і . Однак отриманні результати не дають однозначної відповіді на прийняття ефективного рішення. Для зменшення ризику та більшої впевненості при виборі оптимальної альтернативи надалі використовуємо математичний апарат теорії ймовірності. За умовою задачі відомо, що потенційні можливості підприємства у питанні випуску нових видів продукції оцінюють величиною Р₃ = 0,8. Ця величина є суб'єктивною імовірністю і суттєво відрізняється від класичного означення ймовірності. Суб'єктивна ймовірність є мірою можливого відбуття якої-небудь однієї події за умови, що кількісне вираження є результатом особистого експерименту.

Оскільки події S₁ і S₂ утворюють повну групу події, то має місце P(S₁) + P(S₂) = 1. Суб'єктивні ймовірності, що відомі до прийняття рішення, називаються апріорними ймовірностями. Зрозуміло, що інвестор прийме рішення щодо проведення дослідження ринку попиту, тоді цим він дає зрозуміти про використання отриманих результатів в прийнятті рішення.

При одержанні позитивного висновку з проведеного дослідження (Q₁) інвестор у подальшому повинен звернути увагу на ступінь достовірності результатів. Отже, ймовірність того, що за сприятливого рішення продукція П₁ або П₂ будуть мати попит, становить .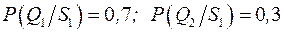

Провівши аналогічні міркування щодо негативного висновку, одержимо:

.

Наступним кроком аналізу дій буде обчислення умовних імовірностей

.

Для їх знаходження використаємо формулу Байєса:

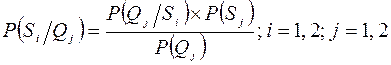. (12.13)

Враховуючи конкретні числові значення, отримаємо:

Оскільки має місце рівність , отримаємо:

.

Звідси, ймовірності відповідних подій будуть: . Отримавши значення P(Q₁) i P(Q₂), обчислимо:

Перейдемо до знаходження оптимального рішення, тобто нам необхідно одержати оптимальну альтернативу дій інвестора. Під оптимальною альтернативою будемо розуміти таке рішення, яке за описуваних умов дає інвестору найбільший річний приріст прибутку. Опишемо алгоритм аналізу оптимальної альтернативи дій інвестора для дискретного випадку з допомогою таких етапів.

Етап 1. Маючи числові значення кінцевих станів , обчислимо для станів 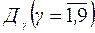відповідні очікувані величини .

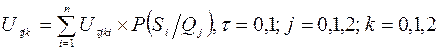. (12.14)

Покажемо, наприклад, розрахунок очікуваного прибутку для стану Д₅:

.

Аналогічно обчислимо інші значення cтанів .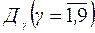

Етап 2. Для кожного стану C_j(0, 1, 2)вибираємо вітку Z_k, що дає найбільше значення очікуваного приросту:

.

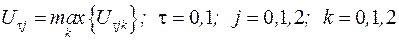Так, наприклад, для стану С₁ маємо:

.

Аналогічно проводять обчислення для інших станів.

Етап 3. Для кожного наступного стану обчислюємо максимально очікуваний приріст прибутку:

.

Наприклад, .

Етап 4. Повернувшись у початковий стан А, вибираємо таку вітку, яка дає максимально очікуваний приріст: .

Таким чином, ми отримаємо оптимальну стратегію прийняття інвестиційного рішення. У нашому випадку маємо:

.

Отже, аналіз показує, що найбільший очікуваний приріст прибутку становитиме 42,96 млн. грн. Звідси, оптимальною альтернативою буде замовлення дослідження щодо прогнозу ринку попиту. Незалежно від висновку, інвестору необхідно вкласти кошти у впровадження виробництва продукції П₂. Зазначений висновок пояснюється тим, що, при прийнятті позитивного прогнозу щодо ринку попиту (подія Q₁), ми потрапимо на вітку С₁Д₆(випуск продукції П₂), а у випадку негативного висновку (подія Q₂) – переходимо на вітку С₂Д₉(випуск продукції П₂), оскільки найбільша очікувана корисність буде 42,96 млн. грн.