E) нет таких
Какая из приведенных систем логических функций не является функционально полной?
D) {x 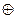 y, 0, 1}
y, 0, 1}
Совершенная дизъюнктивная нормальная форма (СДНФ) логической функции f(x,y,z) = 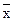
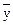 V(x y
V(x y 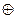 z) имеет вид
z) имеет вид
A) 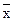 &
& 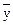 &
& 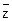 V
V 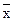 &
& 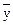 &z V
&z V 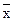 &y&z V x&
&y&z V x& 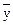 &z V x&y&
&z V x&y& 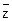
Пусть Х и Y - два множества, |X|=4, |Y|=7. Сколько существует инъективных отображений X®Y?
B) 840
В матрице указаны веса ребер связного неориентированного шестивершинного графа. Найдите вес остовного дерева минимального веса.
¥ 2 2 2 2 2
2 ¥ 4 1 6 8
2 4 ¥ 9 3 5
2 1 9 ¥ 1 4
2 6 3 1 ¥ 3
2 8 5 4 3 ¥
E) 9
Найдите цикломатическое число графа, заданного множеством вершин X={ 0, 1, 2, 3, 4, 5 } и отношением на этом множестве 4=< x+y<=6.
D) 2
Найдите хроматическое число графа, заданного множеством вершин X={0, 1, 2, 3, 4, 5 } и отношением на этом множестве 4=< x+y<=6.
B) 2
Найдите диаметр графа, заданного множеством вершин X={ 0, 1, 2, 3, 4, 5 } и отношением на этом множестве 4=< x+y<=6.
A) 3
На контрольной по математике в группе из 25 человек было предложено два типа задач - по алгебре и по геометрии. Алгебраические задачи решили 18 человек, геометрические- 15 человек, и алгебраические, и геометрические-10 человек. Сколько человек не решили ничего?
E) 2
Укажите множество всех существенных переменных функции
f(x,y,z)=((x®y) (z®y))~(xz®y)
E) {x,y,z}
Полином Жегалкина для функции f(x, y) = x V 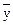 имеет вид
имеет вид
B) 1 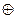 y
y 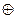 xy
xy
Какая из приведенных функций тождественно ложная?
D) a & 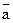
Сколько всевозможных подмножеств содержит множество
F = {0, 2, 4, 6, 8, 10, 12, 14, 16}?
D) 512
Сколько существует всевозможных функциональных отображений множества B во множество A?
А ={1, 2, 3, 4} В={5, 6, 7}
B) 64
Сколько пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, если каждая из них в числе встречается не более одного раза?
A) 720
Сколько элементов содержит множество А × В, если А ={7, 2, 3, 5} и В={3, 1, 5}?
D) 12
Из данного множества формул выделите те, которые имеют вид конъюнктивной нормальной формы (КНФ)
1) 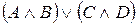 2)
2) 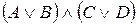 3)
3) 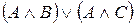
4) 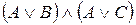 5)
5) 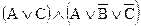 6)
6) 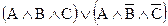
C) 2, 4, 5
Найдите равные множества в данной последовательности:
1) (А \ В) ∩ С 2) (В \ А) ∩ С 3) (А \ С) ∩ В 4) (С \ А) ∩ В 5) (В \ С) ∩ А 6) (С \ В) ∩ А
Дата добавления: 2014-12-06; просмотров: 1348;
