Меры изменчивости (рассеивания, разброса)
Это статистические показатели, характеризующие различия между отдельными значениями выборки. Они позволяют судить о степени однородности полученного множества, о его компактности, а косвенно – и о надежности полученных данных и вытекающих из них результатов. Наиболее используемые в психологических исследованиях показатели: размах, среднее отклонение, дисперсия, стандартное отклонение, полуквартильное отклонение. Размах (Р) – это интервал между максимальным и минимальным значениями признака. Определяется легко и быстро, но чувствителен к случайностям, особенно при малом числе данных.
Примеры: 0, 2, 3, 5, 8 (Р = 8-0 = 8);
-0.2, 1.0, 1.4, 2.0 (Р = 2,0-(-0,2) = 2,2);0,2,3,5,67 (Р = 67-0 = 67).
Среднее отклонение (МД) – это среднеарифметическое разницы (по абсолютной величине) между каждым значением в выборке и ее средним:
МД = ∑d / N,
где d = |Х– M|; М – среднее выборки; X – конкретное значение; N – число значений.
Множество всех конкретных отклонений от среднего характеризует изменчивость данных, но если их не взять по абсолютной величине, то их сумма будет равна нулю. И вся информация пропадает. МД показывает степень скученности данных вокруг среднего. Кстати, иногда при определении этой характеристики выборки вместо среднего (М) берут иные меры центральной тенденции – моду или медиану.
Дисперсия (Д) (от лат. dispersus – рассыпанный). Другой путь измерения степени скученности данных – это избегание нулевой суммы конкретных разниц (d = Х-М) не через их абсолютные величины, а через их возведение в квадрат, и тогда получают дисперсию:
Д = ∑d2 / N – для больших выборок (N > 30); Д = ∑d2/ (N-1) – для малых выборок (N < 30).
Стандартное отклонение (а). Из-за возведения в квадрат отдельных отклонений d при вычислении дисперсии получается очень не наглядная величина, далекая от самих отклонений. Чтобы этого избежать и получить характеристику, сопоставимую со средним отклонением, проделывают обратную математическую операцию – из дисперсии извлекают квадратный корень. Его положительное значение и принимается за меру изменчивости, именуемую среднеквадратическим или стандартным отклонением:
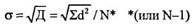
МД, Д и s применимы для интервальных и пропорциональных данных.
Для порядковых данных обычно в качестве меры изменчивости берут полуквартилыше отклонение (Q), именуемое еще полукваргттьным коэффициентом или полумеждуквартильным размахом. Вычисляется этот показатель следующим образом. Вся область распределения данных делится на четыре равные части. Если отсчитывать наблюдения начиная от минимальной величины на измерительной шкале (на графиках, полигонах, гистограммах отсчет обычно ведется слева направо), то первая четверть шкалы называется первым квартилем, а точка, отделяющая его от остальной части шкалы, обозначается символом Q1. Вторые 25% распределения – второй квартиль, а соответствующая точка на шкале – Q2. Между третьей и четвертой четвертями распределения расположена точка Q3. Полуквартильный коэффициент определяется как половина интервала между первым и третьим квартилями:
Q = (Q3 – Q1)/2.
Понятно, что при симметричном распределении точка Q2 совпадет с медианой (а следовательно, и со средним), и тогда можно вычислить коэффициент Q для характеристики разброса данных относительно середины распределения. При несимметричном распределении этого недостаточно. И тогда дополнительно вычисляют еще два коэффициента Q – для правого и левого участков:
Qлев. = (Q2-Q1)/2; Qправ.= (Q3-Q2)/2
Дата добавления: 2014-12-05; просмотров: 991;
