Проблема чотирьох фарб

В математиці теорема про чотири кольори говорить, що будь-яку розташовану на сфері карту можна розмалювати чотирма кольорами так, щоб дві любі області, які мають спільні зони границі, були розмальовані в різні кольори. Ця теорема була сформульована Ф. Гутрі в 1652 р. але довести її не могли довгий час.

Теорема Хівуда(полягає в тому, що будь-який граф можна розмалювати 5 різними кольорами) була доведена в 1890 р. Понизити верхню планку для хроматичного числа будь-якого планарного графа з 5 до 4, тобто підтвердити гіпотезу про чотири кольори не вдавалося майже 90 років. У 1969 р. задача була зведена до розгляду кінцевого, але досить великого числа конкретних випадків, пізніше їх число було скорочене до «всього лиш» 1482. Нарешті в 1976 р. К.Аппель і В.Хейкен за допомогою комп’ютерної програми розібрали всі ці конкретні випадки (витративши на це приблизно 2000 годин роботи потужного на той час комп’ютера). В результаті вони довели наступну теорему.

Теорема про чотири кольори.

Хроматичне число будь-якого планарного графа не перевищує 4.

Доведення цієї теорем стало першим випадком «комп’ютерного» вирішення важкої і давно суто математичної проблеми.

2.4 Точні та евристичні методи розфарбовування графа

В даний час існують методи точного розфарбовування графа. До задачі пошуку оптимального розфарбовування графа зводиться задача пошуку критерію оптимальності для класифікацій спеціального виду h-класифікацій. Точні методи мають експоненціальну складність, їх складність становить O(log(N)) – складність цих алгоритмів різко зростає при збільшенні числа ребер графа N, а також вони дуже громіздкі.

Іншим класом алгоритмів розфарбовування графів є евристичні алгоритми. Вони побудовані на основі однієї чи декількох з наведених теорем:

Теорема 1. Для графа G кількість фарб χ(G)<= k <= n.

Теорема 2. (Кенінга). Граф є біхроматичним (2-х хроматичним), тоді й тільки тоді, коли він не містить непарних простих циклів. З цієї теореми випливає, що будь-яке дерево є біхроматичним.

Для оцінки верхнього значення хроматичного числа графу використовується Теорема Уелша-Пауел. Нехай у графі G вершини впорядковані за спаданням степенів. Тоді

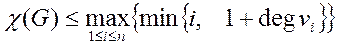
Спільною ознакою евристичних алгоритмів є те, що зазвичай при розфарбовуванні графа послідовно перебираються його вершини, при цьому колір кожної вершини визначається за певним правилом. Необхідно зауважити, що на відміну від точних алгоритмів, результатом евристичних алгоритмів не завжди є оптимальне розфарбовування, тобто може використовуватись більша кількість кольорів, ніж мінімально необхідна.[4]