Вторая вкладка
Вторая вкладка «Распределение частиц» см. Рисунок 3.
В качестве начальных условий здесь указываются:
После ввода всех условий, необходимо нажать кнопку «Создать частицы», тогда программа создаст случайным образом частицы, которые будут отражены в элементе panel.
Частицы на панели отрисовываются с помощью встроенного метода DrawEllipse, принадлежащего библиотеке System.Drawing.Graphics. Диаметр частиц и их положение определяются с помощью генератора случайных чисел.
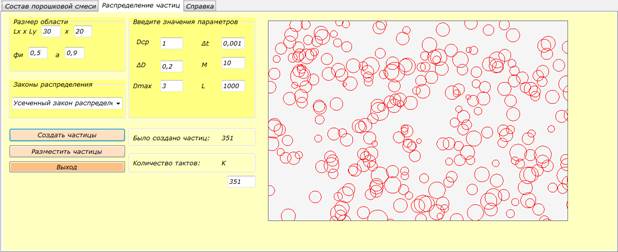
Рисунок 5. Создание частиц
При нажатии на кнопку «Разместить» с помощью метода вязкой суспензии частицы распределяются и занимают все доступное пространство.
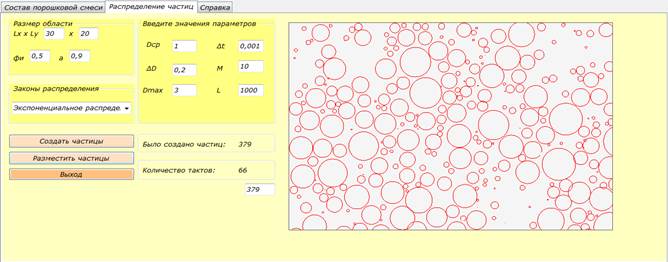
Рисунок 6. Размещение частиц
В качестве результатов исследования выводятся количество созданных частиц и число тактов, за которое частицы были распределены в пространстве.
ИССЛЕДОВАНИЕ
Целью исследования является, анализ скорости заполнения пространства частицами при различных значениях плотности «φ» и коэффициента «а» для усечено нормального распределения.
Для этого были проведены исследования в диапазоне параметров;
Ø 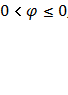 ,
,
Ø  .
.
При больших значениях φ и малых значениях а количество тактов очень большое. Для плотности φ = 0,8 число тактов очень велико даже при а близком к 1.
Я получила такие данные:
Таблица 1. Анализ скорости заполнения пространства частицами
| a/фи | 0,5 | 0,6 | 0,7 | 0,8 |
| 0,1 | ||||
| 0,2 | ||||
| 0,3 | ||||
| 0,4 | ||||
| 0,5 | ||||
| 0,6 | ||||
| 0,7 | ||||
| 0,8 | ||||
| 0,9 | ||||
Исходя из этих данных, были построены следующие зависимости:
При 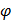 = 0,5
= 0,5

Рисунок 7. Зависимость скорость от «фи = 0,5»
При 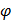 = 0,6
= 0,6
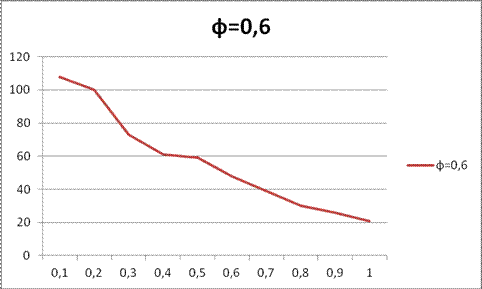
Рисунок 8. Зависимость скорости от «ф=0,6»
При 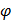 =0,7
=0,7
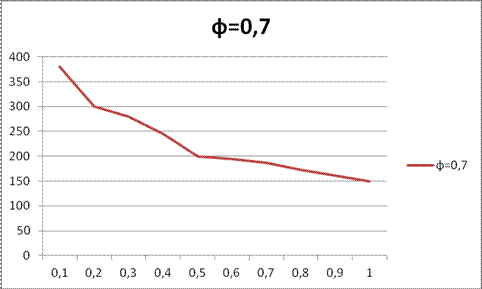
Рисунок 9. Зависимость скорости от «фи=0,7»
ВЫВОДЫ
В ходе курсовой работы был исследован метод вязкой суспензии для моделирования структуры дисперсных систем. Также был изучен метод Монте-Карло для моделирования частиц, используя различные распределения:
· Усеченной нормальное распределение;
· Гамма распределение;
· Экспоненциальное распределение;
· Логнормальное распределение.
Была создана компьютерная программа, реализующая следующие функции:
· Моделирование частиц в соответствии с заданными распределениями методом Монте-Карло.
· Моделирование размещения частиц в области с заданными размерами с помощью метода вязкой суспензии в соответствии с заданными распределениями методом Монте-Карло.
В ходе разработки программы были изучены и освоены некоторые функции языка C# и среды разработки Microsoft Visual Studio 2013:
Ø Компонент ZedGraph для построения графиков функций;
Было проведено исследование скорости размещения частиц в пространстве, в зависимости от плотности распределения, и значений параметров. Полученные результаты показали, что с возрастанием плотности «φ» и уменьшением параметра скорости «a» скорость размещения частиц в пространстве уменьшается. Для уменьшения времени расчетов при заданной плотности, параметр a должен быть равен 1.
СПИСОК ЛИТЕРАТУРЫ
1. Рашковский С.А., Курс лекций по предмету «Математическое моделирование сложных молекулярных структур». 2014 г.
2. Википедия — свободная энциклопедия [ru.wikipedia.org/wiki].
3. Шпаргалка по ZedGraph [jenyay.net/Programming/ZedGraph].
Дата добавления: 2014-11-29; просмотров: 1323;
