П3. Определение параметров прямой линии, проведенной через совокупность точек по методу наименьших квадратов

Пусть имеется совокупность m точек с координатами (x_i, y_i), причем значимость каждой точки совокупности одинакова. Через эти точки необходимо провесим прямую линию

y = a + bx.

Для того, чтобы прямая линия как можно ближе соответствовала всей совокупности точек, должно быть выполнено условие минимального отклонения ординаты прямой при данной абсциссе x_i от истинной ординаты y_i или [y_i –(a + bx_i)] ® 0.

Это условие выполняется для всей совокупности точек, поэтому

.

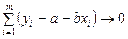Полученное выражение не учитывает возможность появления больших отклонений противоположных знаков, сумма которых может быть близка к нулю. Поэтому удобнее пользоваться квадратами отклонений, имеющими только положительные значения. В этом случае обеспечивают минимизацию квадрата отклонений или

.

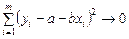Для определения минимума этого выражения его дифференцируют по параметрам a и b, а полученные соотношения приравнивают к нулю.

Таким образом, определение параметров прямой линии a и b сводится к решению системы двух уравнений с двумя неизвестными

.

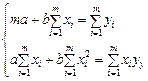Решив систему уравнений, получают

; .