РАСПРЕДЕЛЕНИЕ РАССЕЯННОГО В СРЕДЕ ИЗЛУЧЕНИЯ
Если рассеянное в защите излучение не попадает в точку детектирования, то для любой характеристики Gнр нерассеянного поля излучения, определяемой частицами, не претерпевшими взаимодействия - мощности дозы, плотности потока энергии или частиц, флюенса и др. - можно записать простое соотношение:
 , (5.12)
, (5.12)
где G0 - характеристика поля в отсутствие защиты; Gнр - то же при наличии защиты; d - толщина защиты; m - линейный коэффициент ослабления. Если детектор регистрирует только нерассеянное излучение, говорят о «хорошей геометрии» измерений, или об измерениях в геометрии узкого пучка.
 В реальных задачах всегда наряду с нерассеянным излучением регистрируется и многократно рассеянное в защите излучение. Геометрию, при которой детектор регистрирует нерассеянные и рассеянные частицы, называют геометрией широкого пучка (рис. 5.4). Бывает, что вклад в мощность дозы от рассеянного излучения может многократно (иногда в несколько тысяч раз) превосходить вклад от нерассеянного. Обычно этот вклад учитывается введением в соотношение (5.12) множителя В:
В реальных задачах всегда наряду с нерассеянным излучением регистрируется и многократно рассеянное в защите излучение. Геометрию, при которой детектор регистрирует нерассеянные и рассеянные частицы, называют геометрией широкого пучка (рис. 5.4). Бывает, что вклад в мощность дозы от рассеянного излучения может многократно (иногда в несколько тысяч раз) превосходить вклад от нерассеянного. Обычно этот вклад учитывается введением в соотношение (5.12) множителя В:
 , (5.13)
, (5.13)
где В(Еg, md, z) - фактор накопления, зависящий от характеристик источника излучения, материала защиты и ее толщины, а также от компоновки защиты.
Таким образом, фактор накопления равен кратности превышения характеристик поля нерассеянного (Gнр) и рассеянного (Gр) излучения над характеристиками поля нерассеянного g-излучения:
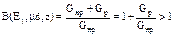 . (5.14)
. (5.14)
Для различных регистрируемых характеристик поля излучения различают фактор накопления: числовой (для плотности потока g-квантов), энергетический (для плотности потока энергии g-квантов), дозовый (для экспозиционной дозы), поглощенной энергии (для поглощенной в среде энергии).
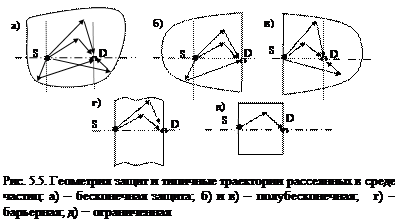 Различные виды геометрий защит приведены на рис. 5.5: бесконечная, полубесконечная, барьерная и ограниченная. Если добавление дополнительных слоев снаружи защиты не изменяет показаний детектора, то тогда защита может считаться бесконечной. Как правило, это означает не менее 4 - 6 длин свободного пробега3 за детектором или источником по линии, их соединяющей, и 2 - 3 длины свободного пробега перпендикулярно к этой линии. В дальнейшем расстояние будем измерять в безразмерных единицах md (d - толщина защиты), поскольку так удобнее сравнивать легкие и тяжелые материалы. Значение md = 1 соответствует толщине защиты, равной длине свободного пробега
Различные виды геометрий защит приведены на рис. 5.5: бесконечная, полубесконечная, барьерная и ограниченная. Если добавление дополнительных слоев снаружи защиты не изменяет показаний детектора, то тогда защита может считаться бесконечной. Как правило, это означает не менее 4 - 6 длин свободного пробега3 за детектором или источником по линии, их соединяющей, и 2 - 3 длины свободного пробега перпендикулярно к этой линии. В дальнейшем расстояние будем измерять в безразмерных единицах md (d - толщина защиты), поскольку так удобнее сравнивать легкие и тяжелые материалы. Значение md = 1 соответствует толщине защиты, равной длине свободного пробега  . Очевидно наибольший фактор накопления будет для бесконечной геометрии, он уменьшается по мере ограничения защиты, поскольку становится меньше возможностей для рассеяния и попадания рассеянного излучения в детектор.
. Очевидно наибольший фактор накопления будет для бесконечной геометрии, он уменьшается по мере ограничения защиты, поскольку становится меньше возможностей для рассеяния и попадания рассеянного излучения в детектор.
В различных справочниках по защите от ионизирующих излучений приводятся численные значения факторов накопления для различных характеристик поля излучения и материалов в бесконечной геометрии. Фрагмент такой таблицы, содержащей значения, необходимые для данной работы, приведен в табл. 5.2.
Таблица 5.2
Дозовые факторы накопления g-излучения с энергией 0,661 МэВ (137Cs) для точечного изотропного источника в бесконечной среде
 
| 0,5 | ||||||||||
| Al | - | 2,18 | 3,85 | 8,2 | 30,0 | - | |||||
| Fe | 1,45 | 1,94 | 3,04 | 5,8 | 18,5 |
Значения факторов накопления получают из решения кинетического уравнения переноса излучения численными методами. Существует множество эмпирических формул, аппроксимирующих значения фактора накопления в различных средах при различных энергиях. Наиболее удобная форма аналитического представления факторов накопления для бесконечной геометрии была предложена Тейлором:
 , (5.15)
, (5.15)
где коэффициенты А1, a1, a2 зависят только от Еg и z материала и не зависят от толщины защиты md. Значения А1, a1, a2 для точечного изотропного источника и бесконечной геометрии приведены в табл. 5.3. Погрешность формулы Тейлора не превышает 5 – 8 %.
Наиболее часто для защиты от изотопных источников применяется барьерная защита. Для такой защиты обычно вводится поправка на барьерность в виде множителя к фактору накопления в бесконечной среде. Для энергии Еg = 0,661 МэВ поправка на барьерность d составляет: для алюминия - 0,814, для железа – 0,88.
Энергетическая зависимость факторов накопления для точечного изотропного источника в различных материалах приведена на рис. 5.6. Для легких и средних элементов в данном диапазоне энергий преобладает комптоновское рассеяние и отношение средней энергии рассеянного излучения к энергии первичного растет с 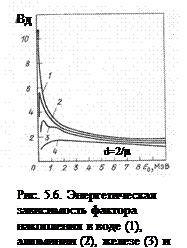 уменьшением энергии. Это приводит к накоплению излучения малых энергий и только за счет фотоэффекта при очень малых энергиях не происходит накопления до бесконечности. Конку-ренцией этих процессов обусловлен пик в области малых энергий. Несколько иначе протекают процессы в тяжелых веществах, например, в свинце. В указанном диапазоне энергий у свинца фактор накопления невелик, т.к. в тяжелых веществах преобладает фотоэлектрическое поглощение. С рос-том энергии влияние фотопоглощения уменьшается и фактор накопления растет. При небольшой толщине среды значение фактора накопления проходит через максимум в области ~ 1 - 2 МэВ, а затем уменьшается с ростом Еg (происходит поглощение g-квантов за счет образования пар).
уменьшением энергии. Это приводит к накоплению излучения малых энергий и только за счет фотоэффекта при очень малых энергиях не происходит накопления до бесконечности. Конку-ренцией этих процессов обусловлен пик в области малых энергий. Несколько иначе протекают процессы в тяжелых веществах, например, в свинце. В указанном диапазоне энергий у свинца фактор накопления невелик, т.к. в тяжелых веществах преобладает фотоэлектрическое поглощение. С рос-том энергии влияние фотопоглощения уменьшается и фактор накопления растет. При небольшой толщине среды значение фактора накопления проходит через максимум в области ~ 1 - 2 МэВ, а затем уменьшается с ростом Еg (происходит поглощение g-квантов за счет образования пар).
Таблица 5.3
Коэффициенты А1, a1, a2 для представления фактора накопления
g-излучения по формуле Тейлора
| Коэффициент | Материал защиты | Для энергии 0,661 кэВ |
| А1 | Алюминий | 9,0 |
| Железо | 8,6 | |
| a1 | Алюминий | 0,13 |
| Железо | 0,091 | |
| a2 | Алюминий | |
| Железо | 0,021 |
Зависимость фактора накопления от толщины защиты проявляется в том, что при увеличении толщины фактор накопления вообще возрастает, хотя характер возрастания и причины для легких и тяжелых материалов несколько различны. Для высоких энергий у средних и легких элементов скорость возрастания фактора накопления с толщиной близка к линейной (рис. 5.7 а)). У тяжелых элементов, если Е < Еmin, фактор накопления растет медленно с расстоянием, а при Е > Еmin распространение большинства g-квантов будет определяться не m, а mmin, и фактор накопления на  чинает быстро расти (рис. 5.7 б)).
чинает быстро расти (рис. 5.7 б)).
Зависимость фактора накопления от атомного номера материала проявляется в уменьшении его с ростом Z. Исключение составляют большие энергии (> 3 МэВ) и большие толщины материалов. В этих случаях зависимость фактора накопления от Z вначале растет, проходит через максимум, а затем медленно падает.
Зависимость фактора накопления от взаимного расположения источника, детектора и ограниченной защиты представляет особый интерес при расчете защиты рабочего места в помещении с источником излучения. Существенная разница между фактором накопления при расположении источника вблизи защиты и при достаточном удалении от нее видна на рис. 5.8. Чем меньше первичного излучения попадает в защиту, тем меньше будет фактор накопления. Это обстоятельство широко используется при проектировании защит от источников ионизирующего излучения.
Факторы накопления гетерогенных защит. Большинство реально сооружаемых защит состоит не из одного материала, а из нескольких, размещаемых слоями. Основная трудность в проектировании таких  защит состоит в определении рассеянного компонента излучения. Если на первый слой вещества падает моноэнергетическое излучение, то на второй и последующие - излучение с непрерывным спектром, причем форма спектра зависит от материалов и толщин всех предыдущих слоев. Существует множество полуэмпирических формул для расчета факторов накопления гетерогенных защит.
защит состоит в определении рассеянного компонента излучения. Если на первый слой вещества падает моноэнергетическое излучение, то на второй и последующие - излучение с непрерывным спектром, причем форма спектра зависит от материалов и толщин всех предыдущих слоев. Существует множество полуэмпирических формул для расчета факторов накопления гетерогенных защит.
Физический смысл построения этих формул в том, что для n-го слоя рассматривается зависимость от толщины так, как это было бы, если все предыдущие слои состояли из того же материала, а исходной точкой служит «накопленный» до этого слоя фактор накопления. Графическая интерпретация фактора накопления в случае чередующихся слоев воды и алюминия показана на рис. 5.9. Для численных расчетов может быть применена формула Бродера:
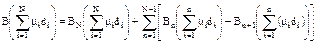 , (5.16)
, (5.16)
где номер слоя i отсчитывается от источника, N - число слоев. Следует заметить, что запись вида 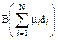 означает, что фактор накопления берется из таблиц или графиков как функция от аргумента
означает, что фактор накопления берется из таблиц или графиков как функция от аргумента  .
.


|
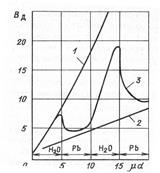
Основной недостаток построения этой формулы в том, что в ней не учитываются переходные эффекты вблизи границ раздела слоев. Влияние граничных эффектов на поведение фактора накопления показано на рис. 5.10. Видно, что при переходе из легкого вещества (воды) в тяжелое (свинец) формула Бродера неприменима. Свинец за счет большого сечения фотоэффекта интенсивно поглощает рассеянное в воде излучение. Для более близких по атомному номеру веществ, например, вода - алюминий или алюминий - железо переходные процессы почти незаметны и формулой Бродера вполне можно пользоваться. В конкретном случае, для двух слоев железо-алюминий формула Бродера расписывается так:
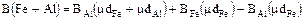 . (5.17)
. (5.17)
Если первый слой – алюминий, второй – железо, в выражении (5.17) надо поменять индексы Al « Fe.
МЕТОДИКА ЭКСПЕРИМЕНТА
Целью настоящей работы является определение дозовых факторов накопления и получение экспериментальных зависимостей факторов накопления различных материалов от толщины защиты. Исследуется влияние на фактор накопления взаимного расположения источника, детектора и защиты. Определяется фактор накопления гетерогенной защиты.
Схема проведения измерений дозового фактора накопления приведена на рис. 5.11. Между источником (1), находящимся в контейнере (2) и детектором (3), устанавливаются алюминиевые или железные пластины (4), рассматриваемые в данном случае как защита. Для измерения мощности экспозиционной дозы используется дозиметр ДРГ-03. В качестве источника g-излучения используется 137Cs, имеющий энергию g-линии 662 кэВ. Толщина алюминиевых пластин d = 0,92 см, железных - 0,74 см, линейный коэффициент ослабления g-излучения в алюминии m = 0,194 см-1, в железе - 0,573 см-1.
Дата добавления: 2014-12-02; просмотров: 3423;
