Подбор функции по опытным данным
Типовые формулы трендов для функций, зависящих от одного аргумента, приведены в подразд. 4.6, и их можно найти с помощью Мастера диаграмм. На диаграмме они приводятся с округленными коэффициентами. Если этой точности недостаточно, коэффициенты данных функций можно найти без построения диаграммы с помощью функций категории Статистические в библиотеке Мастера функций: ЛГРФПРИБЛ(), НАКЛОН(), ОТРЕЗОК(), ПРЕДСК(), РОСТ(), СТОШНЧ(), ТЕНДЕНЦИЯ() и ряда других.
Если требуется подобрать тренд нестандартного типа, можно построить несложный расчетный шаблон для самостоятельного расчета тренда по любой формуле с использованием метода наименьших квадратов. Он представлен на рис. 6.8.1 для тренда, который содержит только два подбираемых коэффициента, например, y = a x + b.
| A | B | C | D | E | F | |
| Таблица функции | Коэффициенты подбираемой функции | |||||
| Опыт | Тренд | Расхождения | а | b | ||
| х | f(х) | у(х) | f(x)-y(x) | |||
| Критерий МНК | ||||||
| S | ||||||
| Среднее расхождение | ||||||
| s | ||||||
Рис. 6.8.1
В столбцах А и В располагается таблица функции, для которой ищется тренд. В ячейки Е3 и F3 введены ориентировочные значения коэффициентов тренда. Эти значения обычно известны по смыслу задачи, и метод наименьших квадратов их только уточняет. Если это не так, то их оценивают с помощью графиков или выбирают произвольные числа в области допустимых значений функции. Начальное приближение, выбранное неаккуратно, просто несколько удлиняет процедуру поиска конечного результата.
В столбец С вводятся формулы тренда, которые используют для коэффициентов ориентировочные значения из ячеек Е3 и F3, а аргумент берут из столбца А "родной" строки (у аргумента – относительный адрес, у коэффициентов – абсолютные).
В столбец D заносятся формулы разности между опытными (f(x)) и расчетными (y(x)) значениями в каждой строке. Чем меньше эти расхождения, тем более удачными являются численные значения коэффициентов, используемых при расчетах. Однако судить о качестве тренда по расхождениям на отдельных точках неудобно. Совокупным критерием (S) качества тренда является сумма квадратов всех расхождений. Чем она меньше, тем в целом ближе расчетные и опытные значения. А тот факт, что расхождения возводятся в квадрат, позволяет на равных учитывать отклонения опыта от расчета как в большую, так и в меньшую стороны. Значение S заносится в ячейку F5, и его удобно рассчитывать с помощью функции СУММКВ() из категории Математические в библиотеке Мастера функций.
И, наконец, последняя, необязательная величина в расчетном шаблоне, это средняя амплитуда отклонения опыта от расчета. Ее можно ввести в ячейку F7 и для простоты оценить по формуле 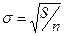 , где n – количество значений функции в таблице. Более точная оценка, учитывающая погрешность коэффициентов тренда, требует знания основ статистики.
, где n – количество значений функции в таблице. Более точная оценка, учитывающая погрешность коэффициентов тренда, требует знания основ статистики.
Дата добавления: 2015-01-02; просмотров: 789;
