ПО ВЫСШЕЙ МАТЕМАТИКЕ
Студента гр _____________
Ф.И.О.
Вариант № ____
Рецензент БИДЕНКО А.Е.
Город, год.
Задача 1. Проверить совместность системы уравнений и в случае совместности решить её: а) по формулам Крамера; б) матричным методом.
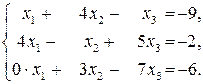
Находим определитель системы:
Так как определитель системы 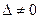 , то система совместна и имеет единственное решение.
, то система совместна и имеет единственное решение.
а) Находим решение по формулам Крамера.
Заменяя в определителе системы столбец коэффициентов при соответствующем переменном столбцом свободных членов, находим определители неизвестных:
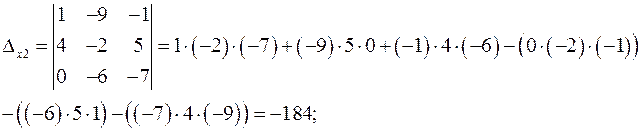
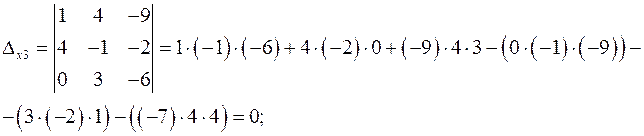 Тогда по формулам Крамера:
Тогда по формулам Крамера:
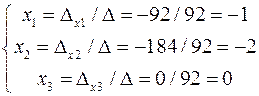
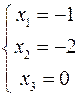
б) Решаем систему уравнений матричным методом:
Запишем матрицу А коэффициентов при неизвестных:
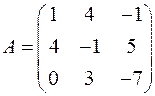
Запишем матрицу-столбец Х при неизвестных:
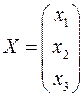
И матрицу-столбец Н свободных членов:
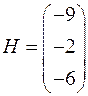
Тогда матричное уравнение 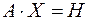 будет эквивалентно исходной системе уравнений, а его решение:
будет эквивалентно исходной системе уравнений, а его решение: 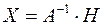 будет одновременно являться и решением исходной системы. То есть, чтобы найти столбец неизвестных Х, надо найти матрицу
будет одновременно являться и решением исходной системы. То есть, чтобы найти столбец неизвестных Х, надо найти матрицу 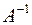 , обратную матрице
, обратную матрице  и справа умножить ее на матрицу свободных членов.
и справа умножить ее на матрицу свободных членов.
Ищем обратную матрицу 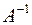 . Обратная матрица
. Обратная матрица 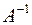 равна:
равна:
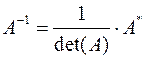 , где:
, где:
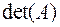 - определитель матрицы
- определитель матрицы  ;
;
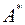 - транспонированная матрица алгебраических дополнений элементов исходной матрицы.
- транспонированная матрица алгебраических дополнений элементов исходной матрицы.
Для матрицы 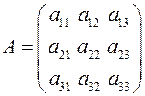 обратная матрица
обратная матрица  будет следующей:
будет следующей:
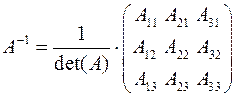
Определитель исходной матрицы А уже найден и он соответствует определителю системы и равен 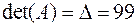 . Ищем алгебраические дополнения элементов исходной матрицы и транспонируем их в матрицу
. Ищем алгебраические дополнения элементов исходной матрицы и транспонируем их в матрицу 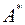 .
.
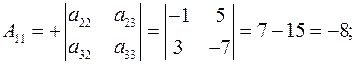
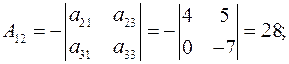
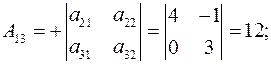
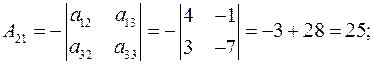
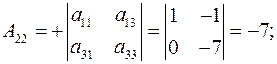
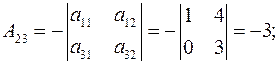
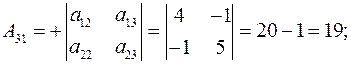

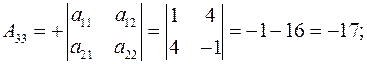
Обратная матрица 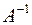 будет:
будет:
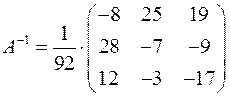
Решение системы линейных неоднородных уравнений 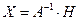 :
:
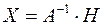



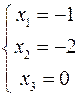
Задача 2. Вершины пирамиды находятся в точках 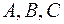 и
и 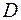 . .А(3; 5; 3); В(-3; 2; 8); С(-3; -2; 6);
. .А(3; 5; 3); В(-3; 2; 8); С(-3; -2; 6);  (7; 8; -2). Вычислить:
(7; 8; -2). Вычислить:
а) площадь грани 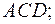
б) площадь сечения, проходящего через середину ребра 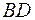 и вершины пирамиды
и вершины пирамиды  и С ;
и С ;
в) объём пирамиды 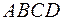 .
.
Решение.
Определим координаты точки  середины ребра
середины ребра  :
:
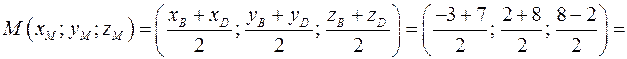 .
.
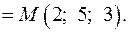
Из вершины  в вершины
в вершины 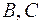 и
и 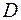 , а также в точку
, а также в точку 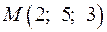 проведем векторы
проведем векторы
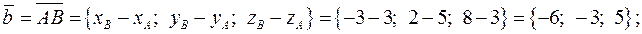
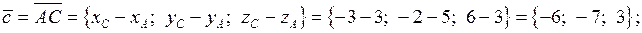
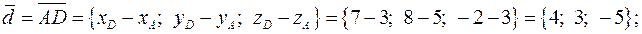
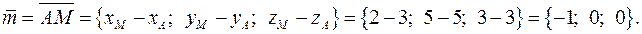
а) площадь грани  равна половине модуля векторного произведения векторов
равна половине модуля векторного произведения векторов 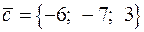 и
и 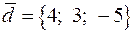 :
:

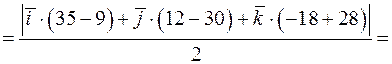
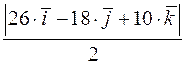 =
=
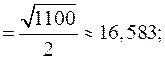
б) площадь сечения, проходящего через середину ребра 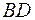 и вершины пирамиды
и вершины пирамиды  и С равна половине модуля векторного произведения векторов
и С равна половине модуля векторного произведения векторов 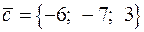 и
и 
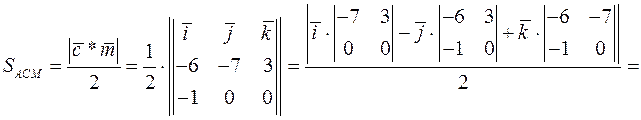
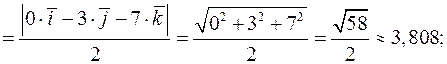
в) объём пирамиды 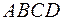 равен одной шестой части смешанного произведения векторов
равен одной шестой части смешанного произведения векторов 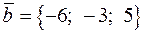 ,
, 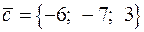 и
и
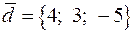 , идущих из одной вершины вдоль граней пирамиды:
, идущих из одной вершины вдоль граней пирамиды:
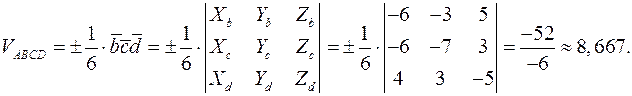
Задача 3. Даны четыре точки: 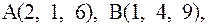
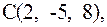
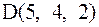 .
.
Составить уравнения:
а) плоскости ABC;
б) прямой AB;
в) прямой DM, перпендикулярной к плоскости ABC;
г) прямой CN, параллельной прямой AB;
д) плоскости, проходящей через точку D, перпендикулярно к прямой AB.
Вычислить:
е) синус угла между прямой AD и плоскостью ABC;
ж) косинус угла между координатной плоскостью Оху и плоскостью ABC.
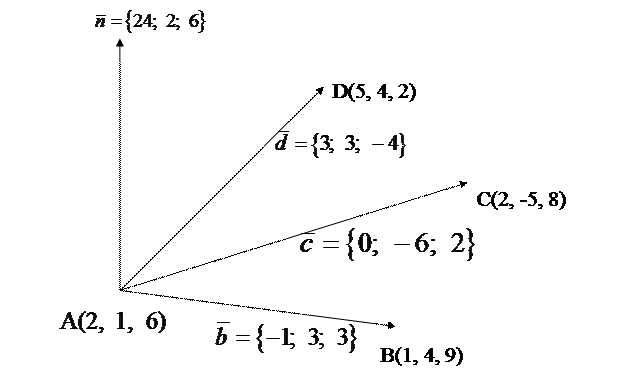
Решение.
Из точки 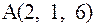 в точки
в точки 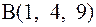 ,
, 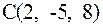 и
и 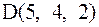 проведем векторы
проведем векторы
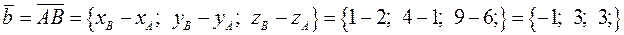
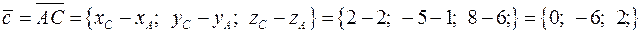

Найдем вектор 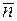 , перпендикулярный к плоскости векторов
, перпендикулярный к плоскости векторов 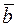 и
и 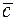 как их векторное произведение:
как их векторное произведение:
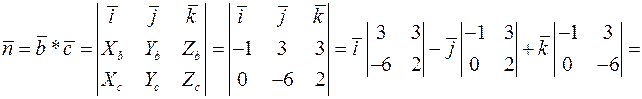

а)Уравнение плоскости ABC, проходящей через фиксированную точку 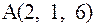 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору 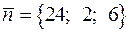 будет:
будет: 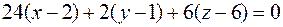 . После сокращения на 2 и приведения подобных членов получим общее уравнение плоскости ABC:
. После сокращения на 2 и приведения подобных членов получим общее уравнение плоскости ABC: 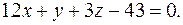
б) Уравнение прямой AB запишем как каноническое уравнение прямой, проходящей через фиксированную точку 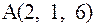 с направляющим вектором
с направляющим вектором 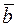
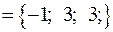 .
.
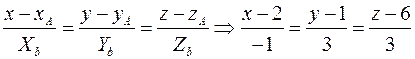 - каноническое уравнение прямой AB.
- каноническое уравнение прямой AB.
в)Уравнение прямой DM, перпендикулярной к плоскости ABC
запишем как каноническое уравнение прямой, проходящей через фиксированную точку 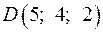 с направляющим вектором
с направляющим вектором
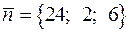 :
: 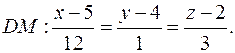
г) Уравнение прямой CN, параллельной прямой AB запишем как
каноническое уравнение прямой, проходящей через фиксированную точку 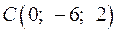 с направляющим вектором
с направляющим вектором
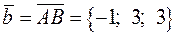 .
. 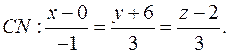
д) Уравнение плоскости, проходящей через точку D,
перпендикулярно к прямой AB. Как общее уравнение плоскости, проходящей через фиксированную точку 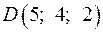 с нормальным вектором
с нормальным вектором 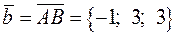 . Ее общее уравнение будет:
. Ее общее уравнение будет:
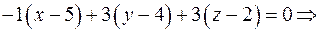
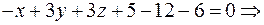
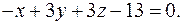
е) Синус угла между прямой AD и плоскостью ABC равен косинусу угла между вектором 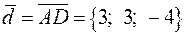 и нормальным вектором
и нормальным вектором 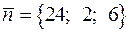 к плоскости ABC:
к плоскости ABC:

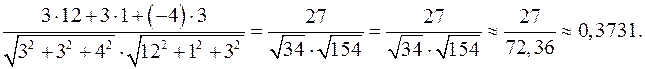
ж) Координатная плоскостью Оху имеет нормальным вектором вектор 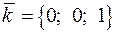 .Косинус угла между координатной плоскостью Оху и плоскостью ABC равен косинусу между векторами
.Косинус угла между координатной плоскостью Оху и плоскостью ABC равен косинусу между векторами 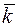 и
и 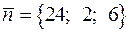 .
.
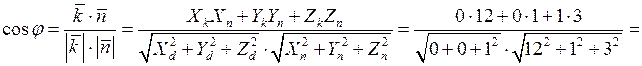
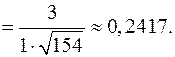
Задача 4Найти пределы не пользуясь правилом Лопиталя
а) 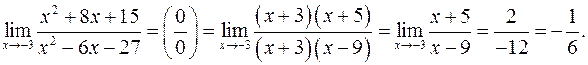
Так как и числитель и знаменатель выражения при 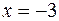 обращаются в нуль, то на основании следствия из теоремы Безу, они раскладываются на множители, среди которых одним из множителей будет
обращаются в нуль, то на основании следствия из теоремы Безу, они раскладываются на множители, среди которых одним из множителей будет 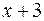 . Для нахождения других множителей производим деление уголком заданных многочленов на
. Для нахождения других множителей производим деление уголком заданных многочленов на 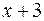 .
.
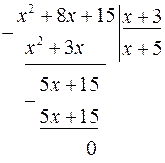
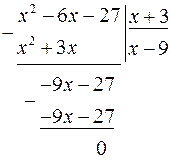
б) 
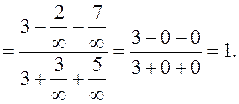
в) 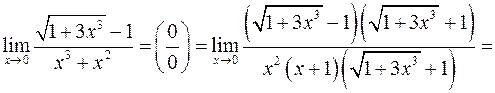
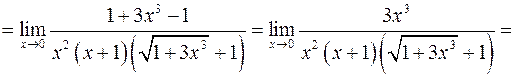
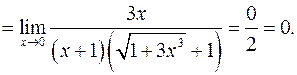
г) 
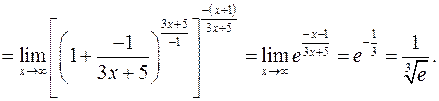
д) 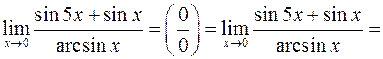
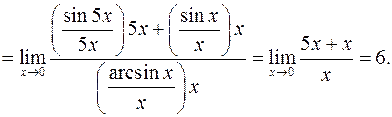
Задача 5. Продифференцировать данные функции
а) 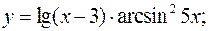

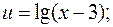
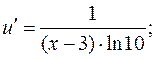
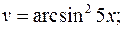
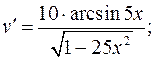
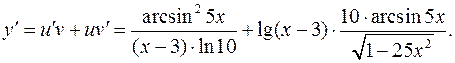
б) 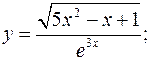
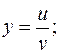
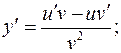
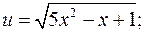
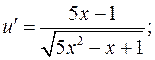
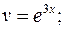
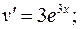
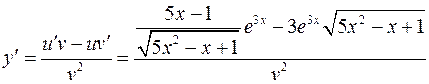
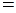
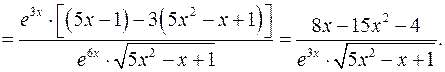
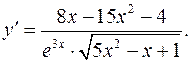
в) 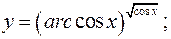 - логарифмическое дифференцирование.
- логарифмическое дифференцирование.
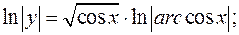
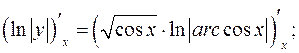
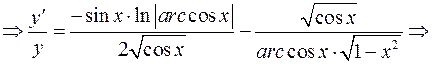
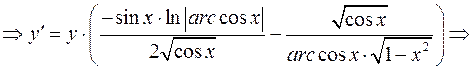
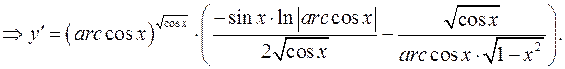
г) 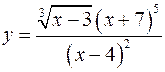 - логарифмическое дифференцирование.
- логарифмическое дифференцирование.
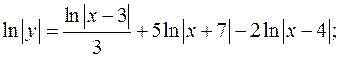
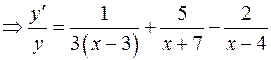
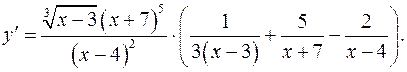
Задача 6. Найти первые и вторые производные  и
и 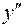 :
:
а) 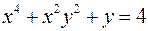 -Неявное задание функции
-Неявное задание функции
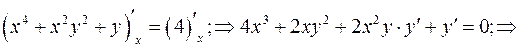
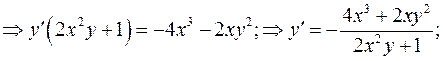
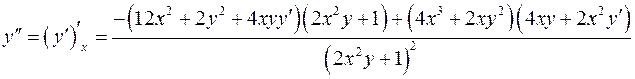 .
.
б) 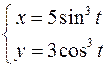 - Параметрическое задание функции
- Параметрическое задание функции
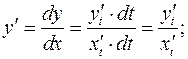
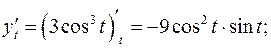
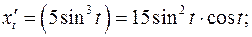
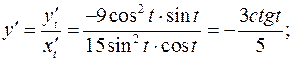
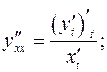
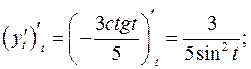
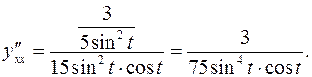
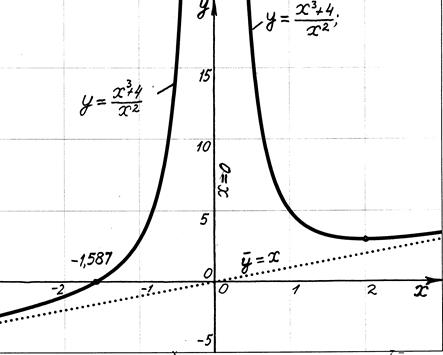
Задача 7. Провести полное исследование функции и построить её график. 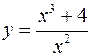
1. Область определения функции: 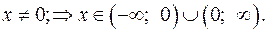
2. Функция общего вида, т.е. не является четной или нечетной, т.к.
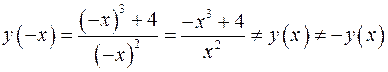 .Т.е. ось
.Т.е. ось  не является осью симметрии и начало осей координат не является точкой симметрии.
не является осью симметрии и начало осей координат не является точкой симметрии.
3. Находим точки пересечения графика функции с осями координат
3.1 Оси  график функции не пересекает, т.к. функция не определена при
график функции не пересекает, т.к. функция не определена при 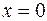 .
.
3.2 Ось 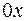 график функции пересекает в том случае, если
график функции пересекает в том случае, если
 .
. 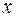 при этом равен
при этом равен 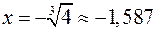 .
.
4. Исследуем функцию на монотонность и экстремумы.
4.1 Находим производную от функции:
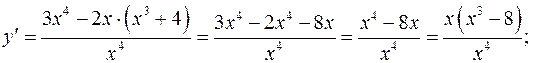
4.2 Находим критические точки функции: 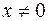 и
и 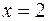 .
.
4.3 Строим таблицу исследования функции на монотонность и экстремумы.
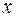
| 
| 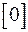
| 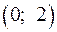
| 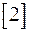
| 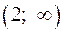
|

| 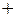
| 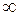
| 
| 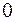
| 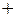
|
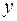
| 
| не определена | 
| min | 
|
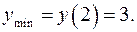
5. Исследуем функцию на выпуклость и вогнутость.
5.1 Находим вторую производную:
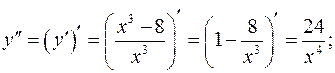
5.2 Критическая точка второго рода: 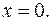
5.3.Строим таблицу исследования функции на выпуклость и вогнутость:
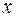
| 
| 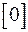
| 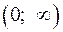
|
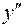
| 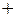
| 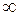
| 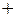
|
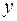
| 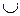
| не определена | 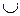
|
6. Исследуем функцию на наличие асимптот.
6.1 Прямая 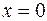 является вертикальной асимптотой, т.к.
является вертикальной асимптотой, т.к.
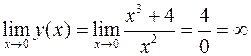 .
.
6.2 Прямая 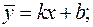 является наклонной асимптотой, если при
является наклонной асимптотой, если при
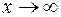 существуют два конечных предела:
существуют два конечных предела:
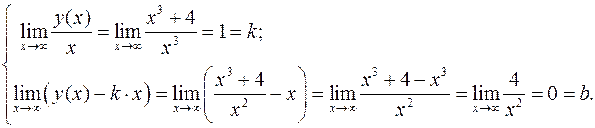
Поэтому прямая 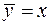 является горизонтальной асимптотой графика функции.
является горизонтальной асимптотой графика функции.
7. Строим график функции 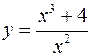
Дата добавления: 2014-12-01; просмотров: 14379;
