Пример 1. Здесь применима теорема о пределе частного
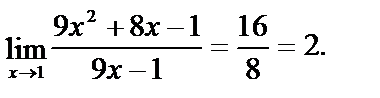
Здесь применима теорема о пределе частного. К этому же выражению при х®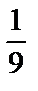 
теорема о пределе неприменима, т. к. 
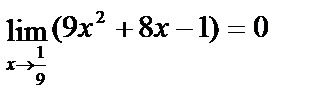и 
.
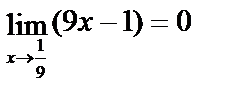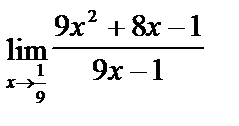представляет собой неопределенность вида 
.
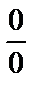Разложим на множители квадратный трехчлен.
9х2+8х–1=9·(х– 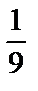)·(х+1).
Для этого достаточно найти корни х1 и х2 квадратного трехчлена
ах2+bх+с=а(х–х1)·(х–х2).
Под знаком предела сократим одинаковые множители и перейдем к пределу:
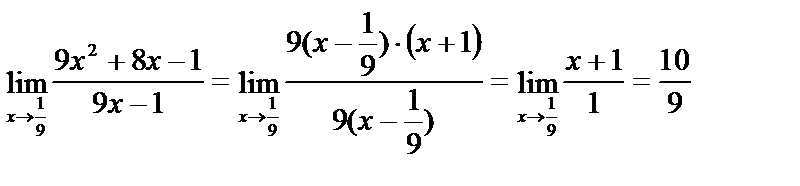
Дата добавления: 2014-12-30; просмотров: 786;