ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ РАЗРУШЕНИЯ
В основу рассматриваемых ниже представлений о «катастрофическом» разрушении положена физическая модель накопления повреждаемости металла в процессе пластической деформации.
Прежде всего, об оценке повреждаемости металла. Известны скалярные и тензорные характеристики повреждаемости. Наиболее широко представлены скалярные характеристики и меры повреждаемости.
В. В. Новожилов показал, что пластическое «разрыхление» можно оценить остаточным увеличением объема металла, т. е., с помощью первого инварианта тензора деформации. Примечательным является вывод об увеличении «разрыхления» пропорционально степени деформации сдвига:
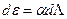 , (1.1)
, (1.1)
где: 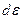 - приращение пластического «разрыхления» элементарного единичного объема деформируемого тела;
- приращение пластического «разрыхления» элементарного единичного объема деформируемого тела;
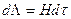 — приращение степени деформации сдвига за малый промежуток времени
— приращение степени деформации сдвига за малый промежуток времени 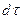 ;
;
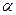 - множитель пропорциональности, определяющий интенсивность
- множитель пропорциональности, определяющий интенсивность
накопления и развития трещин; зависит не только от вида материала, но и от напряженного состояния, температуры и скорости деформации, а также характера протекания деформации (например, знакопеременное деформирование).
Зависимость (1.1) получила подтверждение при экспериментальном исследовании закономерностей пластического «разрыхления» металла, проведенном О. Г. Рыбакиной и Я. С. Сидориным. Ими было установлено, что объемное пластическое «разрыхление» как при циклическом, так и при статическом деформировании увеличивается с ростом пластической деформации 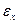 .
.
Будем полагать, что образование макроскопической трещины гриффитсова размера происходит в момент достижения величиной пластического «разрыхления» критического значения 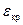 . Степень деформации сдвига, которую претерпела частичка металла к моменту достижения в ней предельного «разрыхления», обозначим
. Степень деформации сдвига, которую претерпела частичка металла к моменту достижения в ней предельного «разрыхления», обозначим 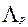 . Поделив правую и левую части уравнения (1.1) на
. Поделив правую и левую части уравнения (1.1) на 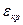 и обозначив левую часть через
и обозначив левую часть через 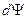 , получим:
, получим:
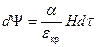 (1.2)
(1.2)
В правой части уравнения 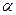 характеризует интенсивность пластического «рызрыхления», следовательно, величина
характеризует интенсивность пластического «рызрыхления», следовательно, величина 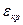 с пластичностью металла
с пластичностью металла 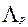 связана простой зависимостью:
связана простой зависимостью:
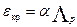 .
.
Подставим это выражение в уравнение (1.2) и проинтегрируем (используем принцип суперпозиции):
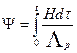 . (1.3)
. (1.3)
Величину 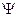 , как условились выше, будем называть степенью использования запаса пластичности металла. Очевидно, что до деформации степень использования запаса пластичности
, как условились выше, будем называть степенью использования запаса пластичности металла. Очевидно, что до деформации степень использования запаса пластичности 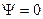 , в момент разрушения
, в момент разрушения 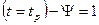 , в любой другой момент
, в любой другой момент 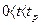 степень использования запаса пластичности
степень использования запаса пластичности 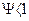 .
.
Таким образом, условие разрушения металла может быть определено в категориях теории пластичности уравнением:
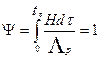 . (1.4)
. (1.4)
Физический смысл этого выражения заключается в достижении величиной пластического «разрыхления» в момент 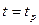 критического значения, после чего происходит образование трещины гриффитсового размера и наступает стадия катастрофического разрушения.
критического значения, после чего происходит образование трещины гриффитсового размера и наступает стадия катастрофического разрушения.
Для того чтобы провести расчет степени использования запаса пластичности металла и определить возможность разрушения металла при том или ином процессе обработки давлением, необходимо последовательно решить ряд задач. Прежде всего определить напряженное и деформированное состояние металла. Для этого необходимо определить траектории движения частиц в очаге деформации, а также значения интенсивности скоростей деформации сдвига Н и показателя напряженного состояния σ/Т вдоль этих траекторий. Эта задача для большинства процессов успешно решается известными в теории, обработки металлов давлением методами. В зависимости от характера задачи применяются как экспериментальные (например, метод визиопластичности), так и теоретические методы. Среди последних широкое распространение полумили инженерный метод, метод линий скольжения и вариационные методы.
Вторая задача связана с определением пластичности металла в зависимости от различных термомеханических параметров.
Результаты исследования пластичности в некоторых случаях с достаточной для практики точностью могут быть представлены параметрическими зависимостями, отражающими связь предельной степени деформации сдвига 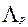 с показателем напряженного состояния (σ/Т), интенсивностью скорости деформации сдвига (Н), температурой
с показателем напряженного состояния (σ/Т), интенсивностью скорости деформации сдвига (Н), температурой 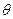 и некоторым показателем немонотонности В:
и некоторым показателем немонотонности В:
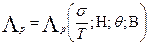 . (1.5)
. (1.5)
В случае, если известны напряженное и деформированное состояния,
т. е. известны Н и σ/Т вдоль траектории движения частиц деформируемого металла, а также зависимость пластичности металла (1.5), то с помощью уравнения (1.3) нетрудно определить степень использования запаса пластичности. Анализ результатов расчета позволяет сделать вывод о возможности разрушения металла при данном процессе обработки металлов давлением и определить в изделии области с наибольшей вероятностью разрушения.
 Лекция № 2.
Лекция № 2.
Тема: ОСНОВНЫЕ НАПРАВЛЕНИЯ ЭКСПЕРИМЕНТАЛЬНОЙ МЕХАНИКИ МАШИН.
Дата добавления: 2014-12-30; просмотров: 1424;
