Введение в предметную область и краткие теоретические сведения

В процессе исторического развития человек все более усовершенствовал орудия своего труда, и все более трудные задачи ему приходилось решать. Техническая необходимость заставляла человека принимать решения в различных сферах своей деятельности, будь то строительство, военное дело, экономика, медицина или игра. На практике человек убедился, что различные решения приводят к различным результатам. Опыт заставлял человека отбрасывать одни решения как негодные, и выбирать из оставшихся решений те, которые приводят к желаемому результату с наименьшими затратами. Имеются в виду не только материальные, но и моральные, этические, правовые и т.п.

Проблема принятия решений или проблема выбора альтернатив - это, может быть, самый распространенный класс задач, с которыми сталкивается не только исследователь, но и инженер-конструктор, хозяйственный руководитель и т.п. И математика, вооруженная современными средствами вычислительной техники, в анализе этих проблем может сыграть выдающуюся роль, но лишь в том случае, если применять ее «правильно».

Любые ситуации, требующие принятия решений, содержат, как правило, большое количество неопределенностей. Их принято разделять на три класса. Прежде всего, это - «неопределенности природы» - факторы нам просто не известные. Затем - «неопределенность противника». Человек всегда существует в условиях, при которых результаты его решений не строго однозначны, они зависят от действий других лиц (партнеров, противников и т.п.), действия которых он не может полностью учесть или предсказать. И, наконец, существуют так называемые «неопределенности желаний» или целей. В самом деле, перед исследователем всегда стоит несколько целей. Описать их одним показателем (критерием) невозможно. Конструктору самолета, например, необходимо обеспечить не только безопасность пассажиров, но и минимальную стоимость перелета. Экономисту нужно построить такой план, чтобы с «минимумом затрат добиться максимума выпуска продукции» и т.п., причем эти требования, как мы видим, часто противоречат друг другу.

Легко понять, что свести подобные задачи с неопределенностями к точно поставленным математическим задачам нельзя. Таким образом, анализ задач принятия решений в условиях неопределенности не может быть завершен силами одних математиков. И всегда умение «эксперта», т.е. профессионала в данной конкретной области, бывает необходимым, а подчас и решающим.

Проблема принятия решений в условиях неопределенности не является математикой, но только математик может изучить все многообразие особенностей этой проблемы и создать системы процедур, которые приведут оперирующую сторону к варианту тех решений, в которых она действительно нуждается.

Если решение принимается в условиях неопределенности, если, например, мы не знаем точно своей цели и результат операции оценивается многими критериями, то и само решение бессмысленно точно фиксировать. Можно говорить о классе «подходящих» решений - не более! Этот факт отчетливо понимается специалистами, и, по существу, он уже давно используется при анализе альтернатив возможных решений. Первым его достаточно четко сформулировал итальянский экономист Парето еще в 1904 году в форме так называемого принципа Парето. Позднее появился еще целый ряд подходов, позволяющих отбраковывать заведомо неприемлемые альтернативы, сузить множество анализируемых вариантов.

Очень важное место в проблемах принятия решений занимает анализ ситуаций, в которых определяющими являются не количественные, а качественные характеристики - холодный, не очень холодный, теплый или красный, темно-красный, почти красный и т.д. Конечно, в каждом конкретном случае для «качественных показателей» можно ввести определенную количественную шкалу - уровень тепла характеризовать градусами, а цвет - длиной волны линии поглощения. Но подобная «метризация» далеко не всегда помогает делу, ибо, во-первых, она вообще не всегда возможна, а во-вторых, не дает достаточно адекватного представления исходной информации. Однако Л. Заде обратил внимание, что этот способ описания особенно удобен при анализе ситуаций с величинами, оцениваемыми качественными характеристиками. Так возникла его теория лингвистических переменных, теория, которая существенно расширяет область традиционных операционалистских исследований. Следующий шаг - это проблема математической обработки той нечеткой информации, которая введена в модель. Для настоящего времени характерно стремление ко все более широкому применению математических методов для описания и анализа сложных экономических, социальных, экологических и других систем. Отличительная особенность многих из этих систем в том, что помимо объективных законов в их функционировании существенную роль играют субъективные представления, суждения и даже эмоции людей. Анализируя конкретную систему, мы фактически рассматриваем выделенную нами часть более полной сложной системы. Само это выделение мы производим, поскольку не в состоянии охватить и достаточно компактно математически описать и исследовать все многообразие свойств полной системы. То, какую часть более полной системы мы выделяем, определяется целями исследования и нашими представлениями о полной системе.

Во многих случаях задача принятия решений в общем виде математически может быть описана множеством допустимых выборов (альтернатив) и заданным на этом множестве отношением предпочтения, которое отражает интересы лица, принимающего решения. Бинарное отношение предпочтения на множестве альтернатив может быть описано в форме так называемой функции полезности.

Следует отметить, что не всякое отношение предпочтения и не на всяком множестве альтернатив можно описать функцией полезности. В некоторых случаях отношение удается описать не одной, а лишь конечным набором функций полезности, причем соответствующие задачи принятия решений обычно называют многокритериальными. Задачи принятия решений, в которых отношение предпочтения описано в форме функций полезности, называют задачами математического программирования. Рациональным решением в таких задачах является выбор допустимой альтернативы, на которой функция полезности принимает по возможности большее значение. Нечеткость в постановке задачи математического программирования может содержаться как в описании множества альтернатив, так и в описании функции полезности.

Нечетким отношением R на множестве X называется подмножество декартового произведения 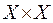, характеризующегося функцией принадлежности :

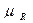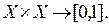
Значение 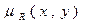этой функции мы понимаем как меру или степень, с которой выполняется отношение R между элементами x и y.