Подавление замираний с помощью пространственно-разнесенного приема
 Если антенн поставить несколько и разнести их в пространстве, то замирание сигнала происходит не одновременно, если принятые сигналы комбинировать, то можно компенсировать замирания, к тому же можно повысить С/Ш. С/Ш будет максимальным, если каждый сигнал с антенны взвешивать с к-том передачи в данном канале связи. Т.к. С/Ш определить сложно, то используют субоптимальные системы. Самая простая – схема автовыбора:
Если антенн поставить несколько и разнести их в пространстве, то замирание сигнала происходит не одновременно, если принятые сигналы комбинировать, то можно компенсировать замирания, к тому же можно повысить С/Ш. С/Ш будет максимальным, если каждый сигнал с антенны взвешивать с к-том передачи в данном канале связи. Т.к. С/Ш определить сложно, то используют субоптимальные системы. Самая простая – схема автовыбора:
 Эта схема не обеспечивает увеличения С/Ш, в отличие от оптимальной схемы. Значительно лучше схема линейного сложения:
Эта схема не обеспечивает увеличения С/Ш, в отличие от оптимальной схемы. Значительно лучше схема линейного сложения:
Как видно сигнал с первой антенны с помощью ФАПЧ фазируется с сигналом второй антенны, а за тем сигналы складываются. Чем больше антенн, тем качественней система подавления замираний, тем выше С/Ш, но и тем сложнее система. Обычно антенн до 16 шт. Существуют еще частотное и поляризационное разнесение.
48.Адаптивная компенсация помех.
Если амплитудно-фазовое соотношение по помеховому компоненту на выходах различных антенн различаются от аналогичных соотношений по сигнальному компоненту, то складывая с определенными весами выходные сигналы антенн можно обеспечить подавление помехового компонента.
Рассмотрим простейшую ситуацию когда одна из антенн направлена точно на источник помехи, а другая на источник сигнала, однако по боковым лепесткам принимает помеху.
 n0(jω)= nип(jω)k0(jω)
n0(jω)= nип(jω)k0(jω)
n1(jω)= nип(jω)k1(jω)
n0(jω)-y(jω)=0
y(jω)=kф(jω)·n1(jω)
Характеристики k0(jω) и k1(jω) описывают частотные характеристики трактов распространения помехи от источника помехи до А0 и от источника помехи до А1. Определим частотную характеристику адаптивного фильтра при которой на выходе вычитающего устройства происходит полное взаимное компенсация помех.
nип(jω)k0(jω)-nип(jω) k1(jω) kф(jω)=0
kф(jω)= 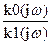
Эта система может подавлять любую помеху.(внеполосные и внутренние помехи)
Из полученного положения следует, что компенсация происходит независимо от формы помехи. Т.к. заранее характеристики k0 и k1 неизвестны и меняются во времени, то фильтр компенсатора помех должен быть адаптивным, и при его разработке решается задача выбора работы фильтра. Если фильтрацию обеспечивать по критерию минимума дисперсии выхода сигнала, то при этом обеспечивается наиболее глубокое подавление помехи.
Обозначим вых. Сигнал через Σ Σ=S + 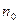 -y
-y
Дисперсия(усреднение по времени) DΣ=  2=
2=  2+
2+ 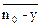 2+
2+ 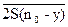 =
= 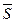 2+
2+ 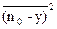
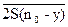 =0 за счет некоррелированности процессов S-сигнала и n-помехи;
=0 за счет некоррелированности процессов S-сигнала и n-помехи;
Из этого следует, что минимум DΣдостигается лишь при обеспечении min 2-ого слагаемого, что означает максимальную взаимную компенсацию процессов n0 и y.
Рассмотрим простейшую реализацию адаптивного фильтра, когда он представляет собой звено с переменным коэффициентом передачи. Определим оптимальное значение коэффициента передачи, который обеспечивает минимум дисперсии сигнала на выходе.
Σ=S +  -ωn ω - коэффициент передачи фильтра;
-ωn ω - коэффициент передачи фильтра;
DΣ= 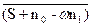 2=
2= 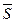 2+
2+ 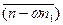 2
2
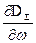 =0
=0 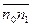 =ωопт
=ωопт 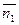 2 ωопт=
2 ωопт= 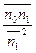
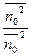 =
= 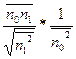 *
* 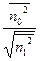 *
* 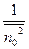
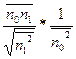 =ρ
=ρ 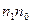
Оптимальные значения коэффициента передачи фильтра определяется степенью коррелированности процесса n0 n1, а также отношением их среднеквадратических значений. Определим степень подавления помехи при использовании данного адаптивного фильтра.
DΣ=(S+ 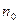 -ωопт
-ωопт 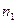 )2=
)2= 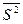 -
- 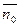 2-2ωопт
2-2ωопт 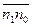 +ωопт2
+ωопт2 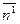 =
= 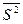 +
+ 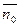 2-2
2-2 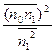 +
+ 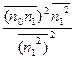 =
=
= 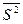 +
+ 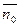 2-
2- 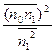 =
= 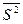 +
+ 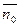 2(1-
2(1- 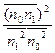 )
)
DΣ= 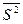 +
+ 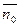 2(1-g)
2(1-g)
Если процессы 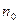 и
и 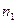 жестко коррелированны, то ρ=0, при этом обеспечивается полное подавление помехи. Если же эти процессы некоррелированы, то подавление помехи отсутствует.
жестко коррелированны, то ρ=0, при этом обеспечивается полное подавление помехи. Если же эти процессы некоррелированы, то подавление помехи отсутствует.
49. Компенсатор узкополосных синфазных помех.
 Совокупность
Совокупность  П2 и ФНЧ образует коррелятор, который вычисляет величину взаимной корреляции между процессами Σ и n1. Σ – это выход компенсатора, а n1 выход антенны на помеху. После инвертировании полярности сигнала выход сигнала коррелятора поступает на усилитель постоянного тока с усилением μ. Выход усилителя с точностью соответствует весовому коэффициенту W, на который умножается сигнал дополнительной антенны n1. В
П2 и ФНЧ образует коррелятор, который вычисляет величину взаимной корреляции между процессами Σ и n1. Σ – это выход компенсатора, а n1 выход антенны на помеху. После инвертировании полярности сигнала выход сигнала коррелятора поступает на усилитель постоянного тока с усилением μ. Выход усилителя с точностью соответствует весовому коэффициенту W, на который умножается сигнал дополнительной антенны n1. В 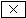 происходит компенсация помехи с выхода сигнала антенны n0 сигналом y. Покажем, что коэффициент ω’ соответствует ωопт , при котором обеспечивается наибольшая компенсация помех.
происходит компенсация помехи с выхода сигнала антенны n0 сигналом y. Покажем, что коэффициент ω’ соответствует ωопт , при котором обеспечивается наибольшая компенсация помех.
ω’= 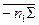 μ; Σ=n0+S+y=n0+S+n1ω’; ω’=
μ; Σ=n0+S+y=n0+S+n1ω’; ω’= 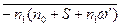 μ= -μ(
μ= -μ( 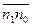 +
+ 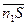 +
+ 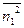 ω’)
ω’)
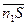 =0 т.к. сигнал и помеха не коррелируемые
=0 т.к. сигнал и помеха не коррелируемые
ω’=-μ( 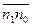 )-μ
)-μ 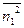 ω’) ω’=
ω’) ω’= 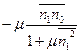
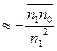 =- ωопт (при μn12>>1)
=- ωопт (при μn12>>1)
Доказано, что данная схема обеспечивает максимально возможное подавление помехи.
Дата добавления: 2014-12-24; просмотров: 919;
