Оптимизация
Оптимизация – это поиск наилучшего в заранее принятом смысле решения из множества допустимых решений. Цель оптимизации выражают целевой функцией, а условие предпочтительности одного решения другому - критерием оптимальности. Критерием оптимальности обычно принимают экстремум целевой функции. Параметры, вариацией которых ищут значение целевой функции, удовлетворяющее критерию оптимальности, называют оптимизируемыми параметрами. Множество допустимых решений получают из множества всех возможных решений заданием ограничений.
В общем виде задачу оптимизации формулируют следующим образом. Найти такие значения оптимизируемых параметров, при которых значение целевой функции удовлетворяет критерию оптимальности, и выполняются ограничения:
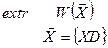 , ,
| (2.4) |
где 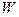 - целевая функция;
- целевая функция;
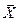 - вектор оптимизируемых параметров;
- вектор оптимизируемых параметров;
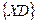 - область допустимых значений оптимизируемых параметров.
- область допустимых значений оптимизируемых параметров.
Рассмотрим постановку задачи оптимизации сортамента проката [4]. Расширение сортамента проката обеспечивает у потребителей значительную экономию металла, снижает трудовые затраты при его обработке, высвобождает мощности металлообрабатывающего оборудования, снижает массу производимых деталей и металлоконструкций. Однако в прокатном производстве затраты увеличиваются: растет дробность заказов, уменьшается размер партии, увеличивается количество и время переналадок стана, возрастает парк сменного оборудования. В связи с этим необходимо выбрать 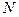 профилеразмеров , характеризуемых параметром
профилеразмеров , характеризуемых параметром 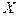 (например, для стали сортовой круглой - диаметром поперечного сечения), которые образуют сортаментный ряд, обеспечивающий минимум суммы затрат при производстве и потреблении:
(например, для стали сортовой круглой - диаметром поперечного сечения), которые образуют сортаментный ряд, обеспечивающий минимум суммы затрат при производстве и потреблении:
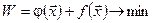 , ,
| (2.5) |
где 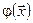 - сумма затрат на производство;
- сумма затрат на производство;
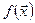 - сумма затрат на потребление;
- сумма затрат на потребление;
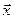 - множество значений параметра, принятого за характеристику профилеразмера (сортаментный ряд):
- множество значений параметра, принятого за характеристику профилеразмера (сортаментный ряд):
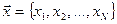 . .
| (2.6) |
Сортаментный ряд 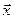 представляет собой набор установленных значений
представляет собой набор установленных значений 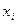 параметра
параметра 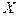 и поэтому с общих позиций стандартизации называется параметрическим рядом. Конкретные значения, образующие всякий параметрический ряд, должны выбираться на основе ряда предпочтительных чиселиз множества предпочтительных чисел
и поэтому с общих позиций стандартизации называется параметрическим рядом. Конкретные значения, образующие всякий параметрический ряд, должны выбираться на основе ряда предпочтительных чиселиз множества предпочтительных чисел 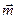 . Поэтому поиск минимума целевой функции (2.4) необходимо выполнять с учетом следующего ограничения:
. Поэтому поиск минимума целевой функции (2.4) необходимо выполнять с учетом следующего ограничения:
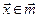 . .
| (2.7) |
В алгоритме стандартизации (рис. 2.1) оптимизация является тем этапом, на котором с помощью строгих экономико-математических методов выбираются конкретные значения параметров объектов стандартизации. Однако, необходимость в ней может появиться вновь как после обработки отзывов на проект стандарта (когда могут быть выявлены важные, но не учтенные ранее факторы), так и по результатам согласования проекта стандарта (когда могут выявиться не учтенные ранее ограничения) [5].
Дата добавления: 2014-12-24; просмотров: 952;
