Воронежский государственный архитектурно-строительный университет
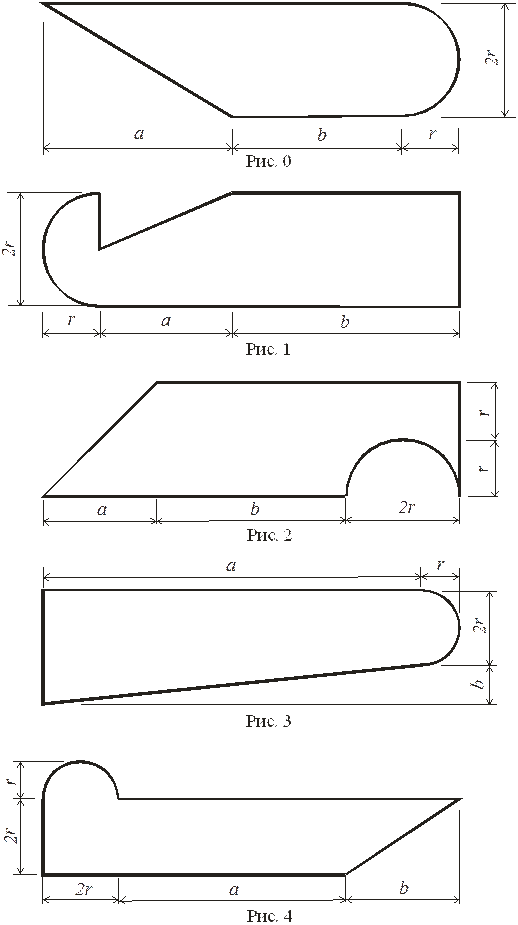
Определить координаты центра тяжести плоской фигуры, изображённой на соответствующем варианту задания рисунке (рис. 0 – 9), с учётом геометрических данных табл. С3.
Указания. Задача относится к теме: определение положения центра тяжести плоских фигур. В решении необходимо применить способ разбиения, при котором плоская фигура разбивается на простейшие части (прямоугольник, треугольник, полукруг), для которых положение центра тяжести известно:
для прямоугольника (квадрата) – на пересечении диагоналей;
для прямоугольного треугольника – в точке пересечения отрезков, проведённых на расстоянии 1/3 длины соответствующего катета ему перпендикулярно от вершины прямого угла;
для полукруга – на оси симметрии полукруга на расстоянии 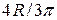 от центра соответствующего круга.
от центра соответствующего круга.
Координаты центра тяжести плоской фигуры определяются по формулам
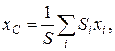
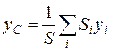 ,
,
где 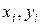 – координаты центра тяжести простейшей части фигуры,
– координаты центра тяжести простейшей части фигуры, 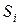 – её площадь,
– её площадь, 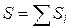 – суммарная площадь.
– суммарная площадь.
Для фигур, имеющих вырезы в виде простейших частей, применяется частный случай способа разбиений – способ дополнения (метод отрицательных площадей).
Пример С3.Определить координаты центра тяжести плоской фигуры, изображённой на рис. С3 при следующих данных: а=40 см, b=100 см, r=20 см.
Решение. Фигура разбивается на три простейшие части: прямоугольник, треугольник, полукруг, площади которых соответственно равны
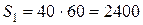 см2,
см2, 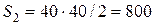 см2,
см2, 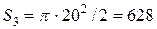 см2.
см2.
Площадь всей фигуры
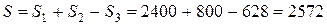 см2.
см2.
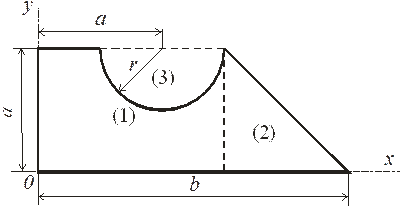
Рис. С3
Центры тяжестей рассматриваемых частей фигуры имеют следующие координаты:
для прямоугольника х1=30 см, y1=20 см;
для треугольника х2=60+40/3=73,3 см, y2=40/3=13,3 см;
для полукруга х3=40 см, y3=40-4·20/(3·π)=31,5 см.
Координаты центра тяжести фигуры в целом вычисляются по формулам
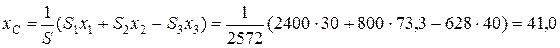 см;
см;
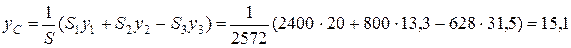 см.
см.
Ответ: xC = 41 см, yC = 15,1 см.
Таблица С3
| Номер условия | ||||||||||
| a, см | ||||||||||
| b, см | ||||||||||
| r, см |
Воронежский государственный архитектурно-строительный университет
Кафедра теоретической механики
Дата добавления: 2014-12-22; просмотров: 1173;
