ДАЛЬНЕЙШИЕ АЛГОРИТМИЧЕСКИЕ РАЗРАБОТКИ

Многими исследователями были предложены улучшения и обобщения описанного выше основного алгоритма обратного распространения. Литература в этой области слишком обширна, чтобы ее можно было здесь охватить. Кроме того, сейчас еще слишком рано давать окончательные оценки. Некоторые из этих подходов могут оказаться действительно фундаментальными, другие же со временем исчезнут. Некоторые из наиболее многообещающих разработок обсуждаются в этом разделе.

В [5] описан метод ускорения сходимости алгоритма обратного распространения. Названный обратным распространением второго порядка, он использует вторые производные для более точной оценки требуемой коррекции весов. В [5] показано, что этот алгоритм оптимален в том смысле, что невозможно улучшить оценку, используя производные более высокого порядка. Метод требует дополнительных вычислений по сравнению с обратным распространением первого порядка, и необходимы дальнейшие эксперименты для доказательства оправданности этих затрат.

В [9] описан привлекательный метод улучшения характеристик обучения сетей обратного распространения. В работе указывается, что общепринятый от 0 до 1 динамический диапазон входов и выходов скрытых нейронов неоптимален. Так как величина коррекции веса Δw_pq,k пропорциональна выходному уровню нейрона, порождающего OUT_p,j, то нулевой уровень ведет к тому, что вес не меняется. При двоичных входных векторах половина входов в среднем будет равна нулю, и веса, с которыми они связаны, не будут обучаться! Решение состоит в приведении входов к значениям ±½ и добавлении смещения к сжимающей функции, чтобы она также принимала значения ±½. Новая сжимающая функция выглядит следующим образом:

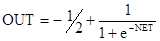. (3.13)

С помощью таких простых средств время сходимости сокращается в среднем от 30 до 50%. Это является одним из примеров практической модификации, существенно улучшающей характеристику алгоритма.

В [6] и [1] описана методика применения обратного распространения к сетям с обратными связями, т. е. к таким сетям, у которых выходы подаются через обратную связь на входы. Как показано в этих работах, обучение в подобных системах может быть очень быстрым и критерии устойчивости легко удовлетворяются.