Виды статистических группировок
В зависимости от ряда признаков выделяют следующие виды статистических группировок (рис.2.2).
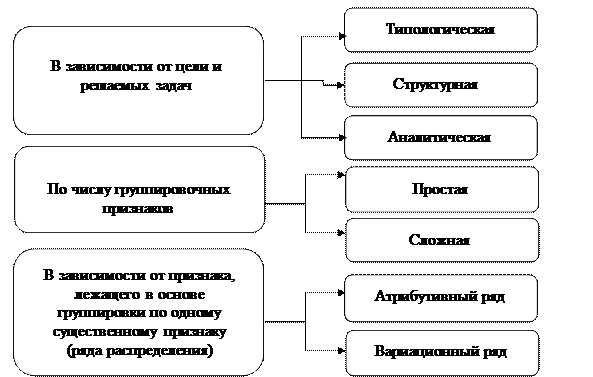
Рисунок 2.2. Виды статистических группировок
1. В зависимости от цели и решаемых задач
1.1. Типологическая группировка – разделение на группы качественно разнородной совокупности на классы, качественно однородные группы. В основу типологической группировки берется качественный (атрибутивный) признак. Например, распределение предприятий по формам собственности, административно-территориальное деление РФ.
1.2. Структурная группировка – разделение однородной в качественном отношении совокупности на группы, характеризующие ее состав и структуру. В основу структурной группировки преимущественно кладется количественный признак (иногда качественный). Например, состав населения по полу, возрасту, распределение крестьянских хозяйств России по размеру земельного участка.
1.3. Аналитическая группировка – выявляет взаимосвязи и взаимозависимости между изучаемыми явлениями и признаками, их характеризующими. В основание группировки кладется факторный (независимый) признак (под воздействием которого изменяются другие – результативные (зависимые)). В каждой группе производится расчет суммарных и средних значений результативного признака.
2. По числу группировочных признаков
2.1. Простые– группировка, в которой группы образованы только по одному признаку. Например, произведена группировка банков по одному признаку – ставке кредитования.
2.2. Сложные– группировка, в которой разбиение совокупности на группы производится по двум и более признакам, взятым в сочетании (комбинации). В свою очередь сложные группировки делятся на комбинационные (два-четыре признака) и многомерные (свыше четырех признаков). Сначала группы формируются по одному признаку, затем группы делятся на подгруппы по другому признаку, а эти в свою очередь делятся по третьему и так далее. Таким образом, сложные группировки дают возможность изучить единицы совокупности одновременно по нескольким взаимосвязанным признакам.
3. В зависимости от признака, лежащего в основе группировки по одному существенному признаку (ряда распределения) (упорядоченное распределение единиц совокупности на группы по определенному признаку).
3.1. Атрибутивные ряды распределения – группировки, образованные по качественному признаку. Примером атрибутивных рядов являются распределения населения по полу, национальности, статусу занятости, образованию и т.д.
3.2. Вариационные ряды распределения – группировки, образованные по количественному признаку. Например, распределение населения по возрасту, сотрудников по стажу работы и уровню заработной платы, домохозяйств – по уровню доходов и расходов и т.д.
Вариационный ряд состоит из двух элементов: вариантов и частот. Под вариантами (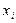 
) понимают конкретные значения признака, которые он принимает в вариационном ряду.
Частоты (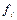 
) – это численности отдельных вариантов или каждой группы вариационного ряда, то есть это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения.
Накопленные частоты (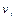 
) показывают число единиц совокупности, у которых значение варианта не больше данного. Сумма всех частот называется объемом совокупности ( 
).
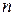Помимо частот в вариационном ряду распределения могут рассчитываться частости ( 
), представляющие собой частоты, выраженные либо в долях единицы, либо в процентах относительно объема совокупности 
.
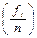Накопленные частости (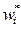 
) рассчитываются как отношение накопленной частоты к числу единиц совокупности и характеризуют долю единиц совокупности со значением не больше данного варианта.
В зависимости от характера вариации вариационные ряды подразделяются на дискретные и непрерывные.
Дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку, то есть признаку, принимающему только дискретные значения, число которых составляет счетное множество. Например, дискретный вариационный ряд может быть построен в случае группировки домохозяйств по числу детей, работающих членов семьи, иждивенцев.
В случае непрерывной вариации, когда величина варьирующего признака может принимать в определенных пределах любые значения, отличающиеся друг от друга на сколь угодно малую величину, целесообразно строить интервальные вариационные ряды.
Значения вариант в интервальных вариационных рядах могут быть как дробными, так и целыми. Значения варьирующего признака в этом случае задаются в виде интервалов. Каждый интервал имеет нижнюю границу (наименьшее значение признака в интервале) и верхнюю границу (наибольшее значение признака в интервале).
Дата добавления: 2014-12-21; просмотров: 1247;