Задачи и примеры к разделу 8
Задача 8.6.1. Расчет горного давления на крепь горизонтальной выработки в режиме заданной нагрузки
Условие задачи
Оценить устойчивость обнажения пород в горизонтальной выработке прямоугольного сечения и определить величину горного давления на крепь, работающую в режиме заданной нагрузки в следующих условиях:
- ширина выработки 2а = 5,5 м;
- высота выработки h = 3 м;
- глубина расположения выработки H = 350 м;
- угол внутреннего трения пород 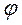 = 30о;
= 30о;
- величина сцепления c = 2 МПа;
- объемный вес пород γ = 26 кН/м3;
- выход керна в кусках 100 мм и более – 20%;
- расстояние между главными нарушениями – 0,3 м;
- характеристика нарушений – сплошные, разделение меньше 1 мм, стенки прочные;
- простирание нарушений относительно оси выработки – перпендикулярно оси выработки;
- направление падения нарушений – от массива к забою;
- угол падения нарушений – 50о;
- приток воды на 10 м выработки – 0 л/мин.
Решение
I.Оценка устойчивости выработки.
Оценка устойчивости выработки ведется по методике ЮАР, т.к. глубина расположения выработки (350 м) не превышает 500 м (максимальная глубина, при которой данная методика может применяться).
По данной методике устойчивость обнажения оценивается суммой баллов по шести факторам:
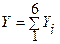 , баллы
, баллы
| где | Y1 | - | фактор, учитывающий прочность породы на одноосное сжатие (приложение 3), баллы; |
| Y2 | - | фактор, учитывающий степень нарушенности породного массива (приложение 4), баллы; | |
| Y3 | - | фактор, учитывающий расстояние между главными нарушениями в массиве (приложение 5), баллы; | |
| Y4 | - | фактор, учитывающий состояние мест нарушений (приложение 6), баллы; | |
| Y5 | - | фактор, учитывающий гидрогеологические условия (приложение 7), баллы; | |
| Y6 | - | фактор, учитывающий направление простирания и падения главных нарушений в породном массиве относительно оси выработки (приложения 8, 9), баллы. |
а) Для определения количества баллов по первому фактору рассчитаем прочность породы на одноосное сжатие Rсж
Для расчета Rсж воспользуемся предельным кругом Мора (рис. 1).
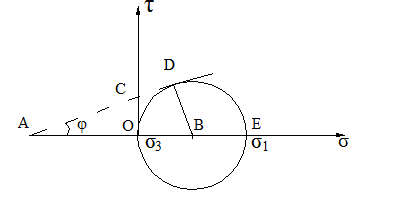
Рис. 1.. Предельный круг Мора
OВ = BЕ = DВ = 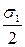 ; AВ = AO + OВ;
; AВ = AO + OВ;
СО = с (сцепление)
AO = 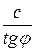 ; AВ =
; AВ = 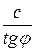 +
+ 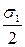 ;
;
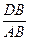 = sinφ;
= sinφ;
sinφ = 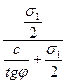 ; sinφ =
; sinφ = 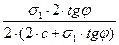 ;
;
σ1 tgφ = 2c sinφ + σ1 tgφ sinφ;
σ1 = 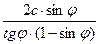 =
= 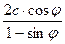
σ1 = Rсж
Следовательно, 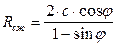 , кгс/см2
, кгс/см2
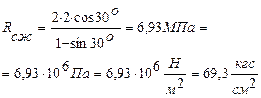
По приложению 3 находим Y1
Y1 = 1 балл (т.к. сопротивление породы одноосному сжатию Rсж находится в пределах > 30 < 100 кгс/см2).
б) По приложению 4 находим Y2
Y2 = 3 балла (т.к. выход керна < 25%).
в) По приложению 5 находим Y3
Y3 = 10 баллов (т.к. величина расстояния между главными нарушениями в массиве находится в пределах > 50 < 300 мм).
г) По приложению 6 находим Y4
Y4 = 20 баллов (т.к. поверхность нарушений слегка шероховатая; разделение < 1 мм; стенки нарушений – прочные).
д) По приложению 7 находим Y5
Y5 = 10 баллов (т.к. приток воды на 10 м выработки = 0 л/мин).
е) По приложениям 8, 9 находим Y6
Y6 = - 5 баллов (т.к. простирание нарушений перпендикулярно оси выработки; падение нарушений – от массива к забою; угол падения нарушений равен 50о).
Y = 1 + 3 + 10 + 20 + 10 – 5 = 39 баллов
По устойчивости породные массивы делятся на V классов. По сумме баллов определяем класс породы (приложение 10). При Y = 39 баллов, класс породы IV (характеристика плохая).
Зная характеристику породы, определим устойчивый пролет выработки АО по графику зависимости величины неподдерживаемого пролета выработки и времени ее устойчивого состояния от класса породы (приложение 11, рис37).
По графику получили, что АО < 5 м при сроке службы < 10 ч.
Следовательно, рассматриваемая выработка шириной 5,5 м нуждается в горной крепи.
II.Определение величины горного давления на крепь со стороны кровли и боков.
В предыдущих задачах были рассмотрены выработки, проводимые в крепких устойчивых породах, и сохраняющие устойчивость без установи горной крепи.
На практике в большинстве случаев для предотвращения обрушения пород в горных выработках необходимо возводить крепь. Крепь препятствует перемещению пород внутрь выработки, а следовательно, воспринимает давление горных пород.
Известно несколько теорий и методов расчета горного давления. К простейшим и дающим достаточно приближенные результаты методикам можно отнести теории проф. М.М Протодьяконова и проф. П.М. Цимбаревича.
По теории проф. М.М. Протодьяконова горное давление рассматривается как внешняя сила, действующая на горную крепь, и равная величине веса пород, входящих в свод естественного равновесия. Т.е. горное давление не зависит от глубины расположения выработки и характеристики крепи, а определяется только шириной этой выработки и коэффициентом крепости породы.
Проф. П.М. Цимбаревич развил теорию проф. М.М. Протодьяконова в применении к выработке с неустойчивыми породами в боках. Высота свода естественного равновесия по проф. П.М. Цимбаревичу определяется с учетом возможного сползания стен выработки (см. рис. 2).
Им же было введено понятия угла внутреннего сопротивления β:
β = arctg f,
где f – коэффициент крепости породы.
Рассмотрим расчет горного давления по теории проф. Цимбаревича П.М.
1. Расчетная схема (рис. 2)

|
b1
h
Рис.2. Расчетная схема для определения величины горного давления со стороны кровли и боков на крепь выработки прямоугольной формы по теории П.М. Цимбаревича.
2. Расчет горного давления со стороны кровли Р.
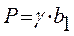 , кПа
, кПа
| где | γ | - | объемный вес пород, кН/м3; |
| b1 | - | высота свода естественного равновесия, м. |
Определим высоту свода естественного равновесия b1:
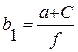 , м
, м
f = tgβ
| где | а | - | половина ширины выработки, м; |
| f | - | коэффициент крепости пород; | |
| β | - | угол внутреннего сопротивления пород, град. |
Из расчетной схемы 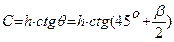 , м
, м
Определим угол внутреннего сопротивления пород 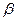 :
:
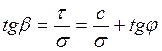 ,
,
| где | 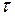
| - | касательные напряжения, МПа; |
| σ | - | нормальные напряжения, МПа; | |
| c | - | величина сцепления пород, МПа; | |
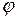
| - | угол внутреннего трения пород, град. |
Определим нормальные напряжения:
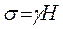 , МПа
, МПа
σ = 26 · 350 = 9,1 МПа
Следовательно, 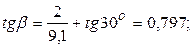
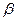 =38,54o
=38,54o
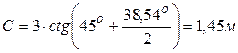
b1 = 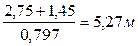
Горное давление со стороны кровли составит:
P = 26 · 5,27 = = 137,0 кПа
3. Расчет горного давления с боков выработки.
Боковое давление на крепь принимается по аналогии давления на подпорную стенку. Т. к. породы, в которых проведена выработка, являются однородными, боковое давление с боков у кровли и у почвы выработки рассчитывается по следующим формулам:
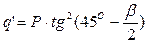 , кПа
, кПа
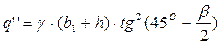 , кПа
, кПа
| где | Р | - | горное давление со стороны кровли, кПа; |
| β | - | угол внутреннего сопротивления пород, град; | |
| b1 | - | высота свода естественного равновесия, м; | |
| h | - | высота выработки, м. |
Боковое давление у кровли q׳:
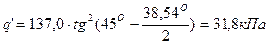
Боковое давление у почвы q׳׳:
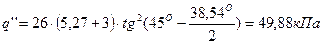
Давление на 1 п.м. выработки D:
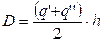 , кН/м
, кН/м
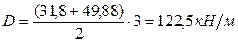
Задание для самостоятельного решения
I. Оценить устойчивость обнажения пород в горизонтальной выработке прямоугольного сечения в условиях, приведенных в табл.1.
II. Определить величину горного давления на крепь, работающую в режиме заданной нагрузки в тех же условиях.
Таблица 1
| Показатели | Варианты | ||
| 1 | 2 | 3 | |
| ширина выработки 2a, м | 6,5 | 6,4 | 5,5 |
| высота выработки h, м | 2,5 | 2,5 | |
| глубина расположения выработки H, м | |||
| угол внутреннего трения пород φ, град | |||
| величина сцепления с, МПа | 2,1 | 1,9 | |
| объемный вес пород γ, кН/м3 | |||
| выход керна в кусках 100 мм и более, % | |||
| расстояние между главными нарушениями, м | 0,4 | 0,35 | 0,25 |
| характеристика нарушений | прерывные, стенки прочные | поверхности сползания открытые | щель меньше 5 мм, заполнены мягким материалом |
| простирание нарушений относительно оси выработки | параллельно оси выработки | параллельно оси выработки | перпендикулярно оси выработки; падение от массива к забою |
| угол падения нарушений, град | 60о | 65о | 45о |
| приток воды на 10 м выработки, л/мин |
Задача 8.6.2. Оценка устойчивости обнажения пород и расчет горного давления на крепь горизонтальной выработки в режиме ее совместной работы с породой
Условие задачи
Оценить устойчивость обнажения пород в постоянной подземной выработке прямоугольного сечения и определить максимальную величину горного давления на крепь, работающую в режиме взаимного влияния крепи и породы, в следующих условиях:
| - ширина выработки вчерне L = 5,5 м; |
| - высота выработки h = 3,0 м; |
| - глубина расположения выработки H = 700 м; |
| - средний объемный вес пород γ = 27 кН/м3; |
| - угол внутреннего трения пород φ = 30о; |
| - величина сцепления с = 3,0 МПа; |
| - выход керна в кусках 100 мм и более - 35%; |
| - гидрогеологические условия - сухая выработка; |
| - параметр расчлененности массива - две системы трещин; |
| - характер мест нарушений – несообщающиеся трещины; |
| - характер изменения пород - неизменные стенки трещин; |
| - состояние породного массива - слабонарушенные породы. |
Толщину слоя разрушенных пород около выработки принять: 0; 0,25 и 0,5 радиуса выработки.
Решение
1.Оценка устойчивости выработки.
Принимая во внимание большую глубину расположения выработки (более 500 м), оценку устойчивости обнажения пород ведем по методике Норвежского института геомеханики.
Оценка устойчивости обнажения породного массива ведется по показателю Q:
Q= 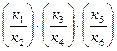 ,
,
где Кi – коэффициенты, определяемые по методике Норвежского института геомеханики (приложения 12 – 17).
По приложению 12 К1 = 35 (выход керна в кусках 100 мм и более - 35%).
По приложению 13 К2 = 4 (две системы трещин).
По приложению 14 К3 = 4 (трещины несообщающиеся).
По приложению 15 К4 = 1 (неизменные стенки трещин).
По приложению 16 К5 = 1 (выработка сухая).
Для определения К6, рассчитаем отношение Rсж/ σ1
Вертикальное напряжение в массиве σ1:
σ1 = γ · Н, МПа
σ1 = 27 · 700 = 18900 кПа = 18,9 МПа
Прочность породы при одноосном сжатии Rсж
Rсж = 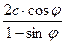 , МПа
, МПа
Rсж = 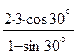 = 10,39 МПа
= 10,39 МПа
Отношение 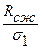 =
= 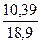 = 0,55
= 0,55
По приложению 17 К6 = 15.
Следовательно, Q = 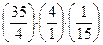 = 2,3
= 2,3
По показателю Q породы массива относятся к IV классу и являются слабыми (приложение 18).
По графику (приложение 19) находим базовый пролет А0 = 3,3 м.
По приложению 20 К7 = 1,6 (т.к. в задаче рассматривается постоянная горная выработка).
Зная К7, определим базовый пролет выработки А:
А = К7 · А0 , м
А = 1,6 · 3,3 = 5,3 м.
Т.к. А (5,3 м) < L (5,5 м), выработка нуждается в установке горной крепи.
2. Расчет максимальной величины горного давления на крепь выработки в режиме ее совместной работы с породой.
В рассмотренных ранее задачах при расчете горного давления учитывался только вес разрушенной породы, и не принимались во внимание такие факторы как усилие, передаваемое от расширяющегося массива, трение внутри разрушенной породы, препятствующее смещению ее в выработку, характеристика крепи и др.
В результате при решении задач были получены лишь приближенные результаты.
В реальных условиях давление на контуре выработки зависит от очень многих факторов, при этом его величина в недостаточно крепкой породе не является постоянной, а меняется и по достаточно сложному закону.
Первопричиной проявления горного давления является напряженное состояние породного массива, окружающего горную выработку. Т.е. разрушение породы на контуре выработки происходит в результате выделения энергии, накопленной массивом.
В упругой крепкой породе радиальное давление на контуре выработки снижается до нуля. Смещение породы в выработку можно принимать за упругое. Выделяемая энергия недостаточна для разрушения породы, в результате выработка остается устойчивой.
При недостаточно крепкой породе давление на контуре выработки меняется в зависимости от величины смещения породы в эту выработку. Следовательно, давление породы на крепь находится в обратной зависимости от величины податливости крепи.
При установке жесткой крепи обеспечивается малое смещение контура выработки, но крепь при этом несет большую нагрузку.
В условиях высокого горного давления целесообразно применение податливых крепей постоянного сопротивления, позволяющих управлять горным давлением путем назначения начального распора крепи, обеспечивающего смещение контура выработки без опасного разрушения окружающих выработку пород. Величина распора крепи устанавливается на основе моделирования взаимодействия крепи с породой в заданных условиях.
Т.к. упругое расширение породы в выработку происходит очень быстро (со скоростью звука), и управлять им мы практически не можем, управляемое давление Р, развиваемое на контуре выработки круглого поперечного сечения, можно считать состоящим из двух частей:
Р = Ра + Рb, МПа
где Ра – давление, возникающее при расслоении пород, окружающих выработку, МПа;
Рb – давление от веса отделившейся от массива породы, МПа.
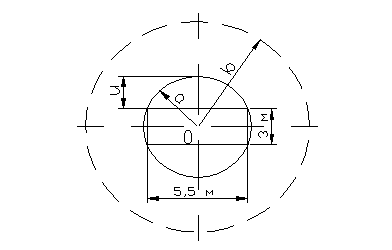
Рис. 4. Расчетная схема к определению горного давления на крепь горизонтальной выработки.
Давление, возникающее при расслоении породы, снижается с ростом величины смещения породы в выработку (т.е. с увеличением толщины слоя разрушенной породы) из-за нарастающей силы трения внутри разрушенного слоя породы.
Если горная порода обладала трением и сцеплением, но при расслоении сцепление породы снизилось до нуля, горное давление, возникающее при расслоении пород, Ра рассчитывается по следующей формуле:
Ра = 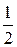
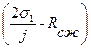 ·(1 – sinφ)·
·(1 – sinφ)· 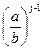 , МПа
, МПа
| где | σ1 | - | вертикальное напряжение в массиве, МПа; |
| j | - | величина, обратная коэффициенту бокового распора; | |
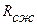
| - | временное сопротивление породы одноосному сжатию, МПа; | |
| φ | - | угол внутреннего трения породы, град.; | |
| а | - | радиус окружности, описанной вокруг поперечного сечения выработки, м (рис. 58); | |
| b | - | радиус окружности расслоившихся пород, м. |
Величина, обратная коэффициенту бокового распора, j:
j = 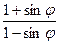
j = 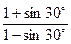 = 3
= 3
j – 1 = 2; j – 2 = 1
Радиус окружности, описанной вокруг выработки, а:
а = 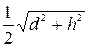 , м
, м
α = 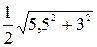 = 3,13 м
= 3,13 м
Рассчитаем горное давление при расслоении пород Ра на контуре окружности радиусом а при толщине слоя разрушенных около выработки пород, равным 0; 0,25 и 0,5 радиуса выработки а.
При b = а
Ра1 = 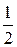 ·
· 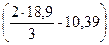 ·(1 – sin 30º)·
·(1 – sin 30º)· 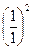 = 0,55 МПа
= 0,55 МПа
При b = 1,25a
Ра2 = Ра1 · 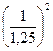 = 0,55 · 0,64 = 0,352 МПа
= 0,55 · 0,64 = 0,352 МПа
При b = 1,5а
Ра3 = Ра1 · 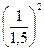 = 0,55 · 0,44 = 0,24 МПа
= 0,55 · 0,44 = 0,24 МПа
Величина давления при расслоении пород постоянна по всему контуру окружности радиуса а.
Давление от веса разрушенной породы растет с увеличением смещения породы в выработку, но темп роста этого давления резко снижается и величина давления приближается к постоянному значению. Давление может стать постоянным достаточно быстро при образовании свода естественного равновесия.
Давление от веса расслоившейся породы Рb вне радиуса а зависит от угла ω иопределяется по формуле:
Рb = 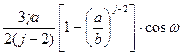 , МПа
, МПа
где ω – угол отсчета от начального положения, град. (см. рис.5).

 0О
0О
 270О 90О
270О 90О
180О
Рис. 5. Расчетная схема определения угла отсчета ω.
Нулевое значение ω будет в кровле, т.к. в этой точке ассиина веса пород является максимальной.
При ω = 0 о cosω = 1;
ω = 90о cosω = 0;
ω = 180о cosω = -1;
ω = 270о cosω = 0.
Следовательно, величина горного давления от веса разрушенных пород будет максимальной сверху контура окружности радиуса а, равной нулю с боков и отрицательной снизу.
Рассчитаем давление от веса разрушенной породы Рb сверху и снизу контура окружности радиуса а для трех случаев.
При b = а давление Р b 1 = 0 МПа
При b = 1,25а
Давление сверху:
Рb2 = 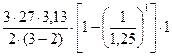 = 25,35 кПа = 0,0254 МПа
= 25,35 кПа = 0,0254 МПа
Давление снизу: Рb2' = -0,0254 МПа
При b = 1,5а
Давление сверху:
Рb3 = 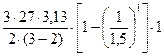 = 41,83 кПа = 0,0418 МПа
= 41,83 кПа = 0,0418 МПа
Давление снизу: Рb3' = -0,0418 МПа
Т.к. рассматриваемая выработка не круглой формы, необходимо рассчитать давление от веса пород внутри радиуса описанной окружности а Рс :
Рс = (γ · u)· cosω, МПа
| где | и | - | высота свода, м; |
| γ | - | объемный вес породы, кН/м3. |
Высоту свода: u = α - 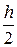 , м
, м
| где | а | - | радиус окружности, описанной вокруг выработки, м; |
| h | - | высота выработки, м. |
u = 3,13 – 1,5 = 1,63 м
Давление от веса пород внутри радиуса а в кровле составит: Рс = (27 · 1,63) · 1 = 44 кПа = 0,044 МПа
В почве Рс ' = - 0,044 МПа
Таким образом, наибольшее давление на крепь выработки Р будет в кровле:
при b = а
Р1 = Ра1 + Рb1 + Рс = 0,55 + 0 + 0,044 = 0,594 МПа
при b = 1,25а
Р2 = Р а2 + Рb2 + Рс = 0,352 + 0,0254 + 0,044 = 0,42 МПа
при b = 1,5а
Р3 = Р а3 + Рb3 + Рс = 0,24 + 0,0418 + 0,044 = 0,33 МПа
С боков выработки будет действовать только давление, возникающее при расслоении пород, Ра; со стороны почвы – давление Ра и давление от веса отделившейся от массива породы, но с отрицательным знаком, т.е. Ра - Рb' – Рс'.
Задание для самостоятельного решения
Оценить устойчивость обнажения пород в квершлаге прямоугольного сечения и определить максимальную величину горного давления на крепь, работающую в режиме взаимного влияния крепи и породы, в условиях приведенных в табл. 3.
Толщину слоя разрушенных пород около выработки принять: 0; 0,25 и 0,5 радиуса выработки.
Таблица 3
| Показатель | Значение по вариантам | ||
| 1 | 2 | 3 | |
| ширина выработки L, м | 6,5 | 5,5 | 6,0 |
| высота выработки h, м | 4,0 | 3,0 | 3,0 |
| глубина расположения выработки H, м | |||
| объемный вес пород γ, кН/м3 | |||
| угол внутреннего трения пород φ, град. | |||
| величина сцепления с, МПа | 2,5 | 2,0 | 2,5 |
| выход керна в кусках 100 мм и более, % | |||
| гидрогеологические условия | сухие выработки | малый приток воды | |
| параметр расчлененности массива | две системы трещин | три системы трещин | две системы трещин |
| характер мест нарушений | несообщающиеся трещины | грубые поверхности контактирующих пород |
Задача 8.6.3. Оценка устойчивости обнажения пород кровли горизонтальной выработки и расчет давления на крепь в режиме заданной деформации
Условие задачи
Оценить устойчивость обнажения пород кровли горизонтальной выработки прямоугольного сечения и определить давление на крепь в режиме заданной деформации в следующих условиях:
| - ширина выработки вчерне L = 4 м; |
| - высота выработки вчерне h = 3,0 м; |
- допускаемая величина осадки крепи 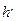 = 0,5 м; = 0,5 м;
|
| - глубина расположения выработки Н = 200 м; |
| - средний объемный вес породы γ = 27 кН/м3; |
| - угол внутреннего трения пород φ = 30о; |
| - величина сцепления с = 1,0 МПа; |
| - выход керна в кусках 100 мм и более - 25%; |
| - расстояние между главными нарушениями в массиве – 0,3 м; |
| - характеристика нарушений – в виде поверхностей сползания, разделенных щелью шириной 2 – 3 мм; простирание нарушений по нормали к оси выработки, угол падения 50о от забоя; |
| - коэффициент разрыхления пород при расслоении К = 1,1; |
| - гидрогеологические условия - приток воды на 10 м длины выработки 50 л/мин. |
Решение
1.Оценка устойчивости обнажения пород кровли выработки.
Принимая во внимание небольшую глубину расположения выработки (200 м), оценку устойчивости ведем по методике ЮАР.
Показатель устойчивости обнажения:
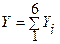 , баллы
, баллы
| где | Yi | - | баллы по учитываемым факторам, определяемым по методике ЮАР (приложения 3 – 9), баллы. |
а) Для определения количества баллов по первому фактору рассчитаем прочность породы на одноосное сжатие Rсж.
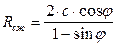 , кгс/см2
, кгс/см2
| где | с | - | величина сцепления, МПа; |
| φ | - | угол внутреннего трения, град. |
Rсж = 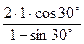 = 3,46 МПа = 34,6 кгс/см2
= 3,46 МПа = 34,6 кгс/см2
По приложению 3 находим Y1
Y1 = 1 балл (т.к. сопротивление породы одноосному сжатию Rсж находится в пределах > 30 < 100 кгс/см2).
б) По приложению 4 находим Y2
Y2 = 3 балла (т.к. выход керна < 25%).
в) По приложению 5 находим Y3
Y3 = 10 баллов (т.к. величина расстояния между главными нарушениями в массиве находится в пределах > 50 < 300 мм).
г) По приложению 6 находим Y4
Y4 = 6 баллов (т.к. характеристика нарушений - в виде поверхностей сползания, разделенных непрерывной щелью шириной < 5).
д) По приложению 7 находим Y5
Y5 = 4 балла (т.к. приток воды на 10 м выработки находится в пределах > 25 < 125 л/мин).
е) По приложениям 8, 9 находим Y6
Y6 = 0 баллов (т.к. простирание нарушений перпендикулярно оси выработки, угол падения нарушений от забоя и находится в пределах > 45о < 90о ).
Сумма баллов: Y = 1 + 3 + 10 + 6 + 4 – 0 = 24 балла
По сумме баллов определяем класс породы (приложение 10). При Y = 24 балла, класс породы IV (характеристика плохая).
Зная характеристику породы, определим устойчивый пролет выработки АО по графику зависимости величины неподдерживаемого пролета выработки и времени ее устойчивого состояния от класса породы (приложение 11, рис. 37).
По графику получили, что АО < 3 м при сроке службы < 5 ч.
Следовательно, рассматриваемая выработка шириной 4 м нуждается в установке горной крепи.
2. Определяем величину горного давления Р на крепь в режиме заданной деформации.
Горное давление на крепь Р :
Р = Ра + Рb+ Рс , МПа
где Ра – давление на контуре описанной окружности радиуса а, возникающее при расслоении пород, окружающих выработку, МПа;
Рb – давление от веса отделившейся от массива породы на контуре описанной окружности радиуса а, МПа;
Рс – давление от веса отделившейся от массива породы на крепь внутри описанной окружности радиуса а, МПа.
Расчетная схема приведена на рис. 6.
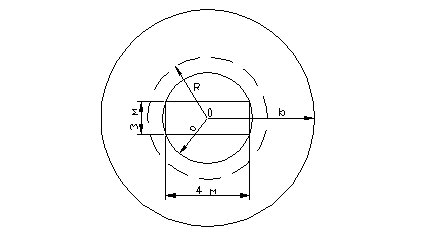
Рис. 6. Расчетная схема к определению горного давление на крепь горизонтальной выработки в режиме заданной деформации.
Горное давление, возникающее при расслоении пород, Ра :
Ра = 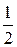
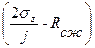 ·(1 – sinφ)·
·(1 – sinφ)· 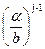 , МПа
, МПа
| где | σz | - | вертикальное напряжение в массиве, МПа; |
| j | - | величина, обратная коэффициенту бокового распора; | |
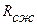
| - | временное сопротивление породы одноосному сжатию, МПа; | |
| φ | - | угол внутреннего трения породы, град.; | |
| а | - | радиус окружности, описанной вокруг поперечного сечения выработки, м; | |
| b | - | радиус окружности расслоившихся пород, м. |
Вертикальное напряжение в массиве σz:
σz = γ · Н; МПа
σz = 27 х 200 = 5400 кПа = 5,4 МПа
Величина, обратная коэффициенту бокового распора, j:
j = 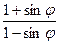
j = 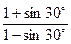 = 3; j – 1 = 2; j – 2 = 1
= 3; j – 1 = 2; j – 2 = 1
Радиус описанной около сечения выработки окружности после осадки крепи а:
а = 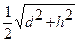 , м
, м
а = 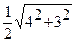 = 2,5 м
= 2,5 м
Радиус описанной около сечения выработки окружности до осадки крепи R:
R = 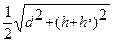 , м
, м
| где | h | - | высота выработки вчерне, м; |
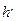
| - | допускаемая величина осадки крепи, м. |
R = 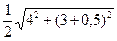 = 2,8 м
= 2,8 м
Отношение 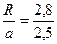 = 1,06
= 1,06
Определим зависимость между начальным радиусом описанной около сечения выработки окружности R, конечным а и радиусом b зоны расслоения пород (см. рис. 6).
Объем (на единицу длины) выработки радиуса b в массиве Vb:
Vb = πb2, м2 на единицу длины
Объем кольца толщиной S в массиве VS:
VS = π · (b2 – R2), м2 на единицу длины
После расслоения породы толщина кольца породы будет S1, его объем составит VS1:
VS1 = KVS = Kπ·(b2 – R2); м2 на единицу длины,
| где | К | - | коэффициент расслоения породы. |
Объем выработки Va после смещения в нее породы при расслоении составит:
Va = Vb – VS1 = π b2 – K π (b2 – R2)=
= π a2, м2 на единицу длины
откуда а2 = Va/π = b2 – K(b2 – R2);
тогда получим R = 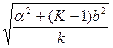 , м Отношение b/a:
, м Отношение b/a:
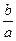 =
= 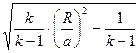 =
= 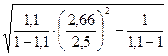 = 1,56
= 1,56
Получим b = 1,56 · а = 1,56 · 2,5 = 3,9 м
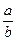 =
= 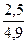 = 0,64
= 0,64
Горное давление Ра на контуре описанной окружности радиуса а при расслоении пород составит:
Ра = 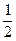 ·
· 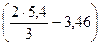 ·(1 – sin 30º) · 0,64 2= 0,014 МПа
·(1 – sin 30º) · 0,64 2= 0,014 МПа
Давление Рb от веса расслоившейся породы на контуре описанной окружности радиуса а определяем по формуле:
Рb = 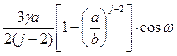 , МПа
, МПа
| где | ω | - | угол отсчета от начального положения, град. (см. задачу 17, рис. 28) |
При ω = 0 о cosω = 1;
ω = 90о cosω = 0;
ω = 180о cosω = -1;
ω = 270о cosω = 0.
Давление от веса расслоившейся породы Рb сверху составит:
Рb = 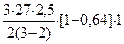 = 56 кПа = 0,056 МПа
= 56 кПа = 0,056 МПа
Снизу Pb' = - 0,056 МПа
Т.к. рассматриваемая выработка не круглой формы, необходимо рассчитать давление от веса пород внутри радиуса а Рс:
Рс = (γ · u)·cosω, МПа
| где | и | - | высота свода, м; |
| γ | - | объемный вес породы, кН/м3; | |
| ω | - | угол отсчета от начального положения, град. |
Высоту свода: u = α - 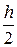 ; м,
; м,
| где | а | - | радиус окружности, описанной вокруг выработки, м; |
| h | - | высота выработки, м. |
Давление от веса пород внутри радиуса а в кровле выработки составит:
Рс = 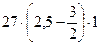 = 27 кПа = 0,027 МПа
= 27 кПа = 0,027 МПа
В почве Рс' = - 0,027 МПа
Таким образом, наибольшее давление на крепь выработки Р будет в кровле:
Р = 0,014 + 0,056 + 0,027 = 0,097 МПа
В боках Р = 0,014 МПа (давление от расслоения пород)
В почве Р = 0,014 – 0,056 – 0,027 = - 0,069 МПа
Задание для самостоятельного решения
Оценить устойчивость обнажения пород кровли горизонтальной выработки прямоугольного сечения и определить давление на крепь в режиме заданной деформации в условиях, приведенных в табл. 4.
Таблица 4
| Показатель | Значение по вариантам | ||
| 1 | 2 | 3 | |
| ширина выработки вчерне L, м | 4,5 | 4,5 | |
| высота выработки вчерне h, м | 3,2 | 3,3 | 3,2 |
| допускаемая величина осадки крепи h', м | 0,6 | 0,6 | 0,5 |
| глубина расположения выработки H, м | |||
| средний объемный вес породы γ, кН/м3 | |||
| угол внутреннего трения пород φ, град. | |||
| величина сцепления c, МПа | 1,0 | 1,05 | 1,0 |
| выход керна в кусках 100мм и более, % | |||
| расстояние между главными нарушениями в массиве, м | 0,4 | 0,4 | 0,3 |
| характеристика нарушений | в виде поверхностей сползания, разделенных щелью шириной 2-3 мм; простирание нарушений по нормали к оси выработки, угол падения 50о | ||
| коэффициент разрыхления пород при расслоении К | 1,1 | ||
| гидрогеологические условия | приток воды на 10 м длины выработки 50 л/мин. |
Дата добавления: 2014-12-21; просмотров: 1546;
