Задачи и примеры к разделу 6
Задача 6.4.1.Оценка несущей способности целика по данным испытаний образцов (детерминированный метод)
Условие задачи
Определить несущую способность целика цилиндрической формы диаметром 5 м и высотой 10 м по результатам испытаний образцов. Целик представлен крепким песчаником, разбитым тремя системами трещин. Расстояние между трещинами 1,5 м. Результаты испытаний образцов на сжатие приведены в табл. 2.
Таблица 2
| Число испытаний n | Размеры образцов, см | Объем образца V, см3 | Среднее значение предела прочности породы сжатию Q, МПа | |
| диаметр d | высота h | |||
| 3,0 | 6,0 | 42,39 | ||
| 3,5 | 7,0 | 67,31 | ||
| 4,0 | 8,0 | 100,48 | ||
| 4,5 | 9,0 | 143,07 | ||
| 5,0 | 10,0 | 196,25 | 115,5 | |
| 5,5 | 11,0 | 261,21 | 113,0 | |
| 6,0 | 12,0 | 339,12 | 111,7 |
Решение
Прочность породы в массиве меньше несущей способности образца породы, т.к. в отличие от образца породный массив имеет различные виды нарушений.
Основными методами определения прочности породы в массиве являются:
- методика Д.Ф. Коутса (для однородного массива);
- методика Г.М. Малахова (для массива, разбитого системой трещин на отдельные блоки);
- методика ВНИМИ (учитывает структурное ослабление массива).
1.Определение прочности структурного блока целика по формуле Д.Ф. Коутса
В данной задаче целик разбит системой трещин на блоки. Блок является однородной структурной единицей целика. Прочность структурного блока QБ определяем по формуле Д.Ф. Коутса.
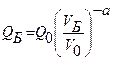 , МПа
, МПа
| где | QБ | - | прочность структурного блока, МПа; |
| Q0 | - | прочность единичного объема по данным испытания образцов той же формы, что и целик, МПа; | |
| VБ | - | объем структурного блока, см3; | |
| V0 | - | единичный объем (V0 = 100 см3); | |
| а | - | коэффициент, зависящий от свойств породы. |
Объем структурного блока VБ:
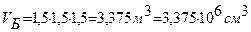
По результатам испытаний образцов строим график зависимости временного сопротивления породы сжатию Q от объема образца V (рис. 1).
Q, МПа

120 
V, см3
Рис. 1. График зависимости прочности образцов от их объема
Из графика (рис. 1) находим прочность единичного объема Q0 и значение коэффициента а.
Q0= 120 МПа (V0 = 100 см3)
а = tg  = 0,05
= 0,05
Прочность структурного блока QБ:
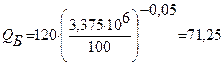 МПа
МПа
2.Определение несущую способность целика QЦ по формуле Г.М. Малахова.
Учитывая, что по условию задачи целик разделен системой трещин на блоки и зная прочность структурного блока, рассчитаем несущую способность целика по формуле Г.М. Малахова:
 , МПа
, МПа
| где | QЦ | - | несущая способность целика, МПа; |
| QБ | - | прочность структурного блока, МПа; | |
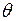
| - | размер исследуемой части массива (диаметр целика), м; | |
| S | - | расстояние между трещинами, м. |
Несущая способность целика QЦ составит:
 МПа
МПа
Задание для самостоятельного решения
Определить несущую способность целика цилиндрической формы диаметром 5 м и высотой 10 м по результатам испытаний образцов, изготовленных из материала целика. Целик представлен крепким песчаником, разбитым тремя системами трещин Расстояние между трещинами 1,3 м. Результаты испытаний образцов на сжатие приведены в табл. 3.
Таблица 3
| Число испытаний n | Размеры образцов, см | Объем образца V, см3 | Среднее значение временного сопротивления породы сжатию Q, МПа по вариантам | |||
| диаметр d | высота h | 1 | 2 | 3 | ||
| 3,0 | 6,0 | 42,39 | ||||
| 3,5 | 7,0 | 67,31 | ||||
| 4,0 | 8,0 | 100,48 | ||||
| 4,5 | 9,0 | 143,07 | ||||
| 5,0 | 10,0 | 196,25 | 112,5 | |||
| 5,5 | 11,0 | 261,21 | 110,0 | |||
| 6,0 | 12,0 | 339,12 | 108,7 |
Задача 6.4.2. Оценка несущей способности целика по прочности образцов (статистический метод)
Условие задачи
Определить несущую способность целика цилиндрической формы диаметром 5 м и высотой 10 м по данным испытаний на сжатие образцов, изготовленных из материала целика. Результаты испытаний образцов на сжатие приведены в табл. 4. Целик представлен крепким песчаником, слегка нарушенным одной системой несообщающихся трещин, расположенных на расстоянии 1,8 – 2 м друг от друга. Уровень риска разрушения целика принять 1%.
Таблица 4
| Число испытаний n | Размеры образца | Объем образца V, см3 | Среднее значение временного сопротивления образца сжатию Q, МПа | Коэффициент вариации VВО, % | |
| диаметр d, см | высота h, см | ||||
| 3,0 | 6,0 | 42,39 | 126,0 | 11,0 | |
| 3,5 | 7,0 | 67,31 | 123,0 | 10,0 | |
| 4,0 | 8,0 | 100,48 | 120,0 | 12,0 | |
| 4,5 | 9,0 | 143,07 | 117,0 | 13,0 | |
| 5,0 | 10,0 | 196,25 | 115,5 | 11,0 | |
| 5,5 | 11,0 | 261,21 | 113,0 | 12,0 | |
| 6,0 | 12,0 | 339,12 | 111,7 | 13,0 | |
| Среднее | 11,7 |
Решение
1.Определение среднего временного сопротивления целика сжатию QЦ0 по формуле Д.Ф. Коутса без учета структурного ослабления,
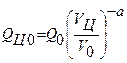 , МПа
, МПа
где VЦ - объем целика, см3
V0 - принятый единичный объем образца, см3;
Q0 - временное сопротивление сжатию образца единичного объема, МПа;
a - коэффициент, зависящий от свойств породы.
Объем целика VЦ:
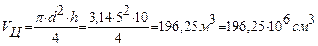
Единичный объем образца принимаем V0 = 100 см3
По результатам испытаний образцов строим график зависимости временного сопротивления Q от объема образца V (см. задачу 6. 4.2, рис. 3).
Из графика (задача 6.4.2, рис. 3) определяем временное сопротивление сжатию единичного объема образца Q0 и значение коэффициента а.
Q0= 120 МПа (V0 = 100 см3)
а = tg  = 0,05
= 0,05
Временное сопротивление сжатию целика без учета его структурного ослабления QЦ0 составит:
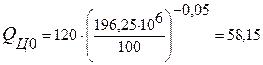 МПа
МПа
1.Определение среднего временного сопротивления целика сжатию с учетом его структурного ослабления QЦ по методике ВНИМИ.
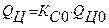 , МПа
, МПа
| где | КС0 | - | коэффициент структурного ослабления целика. |
Из приложения 1 определяем КС0 = 0,9
Следовательно, 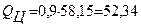 МПа
МПа
2.Определение несущей способности целика статистическим методом QЦ1 при уровне риска его разрушения P = 1%.
Прочность целика распределяется по нормальному закону.

Для уровня риска разрушения целика Р = 0,01 (1%) (рис. 2)
Ф(t )
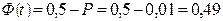
Р = 0,01 (площадь под кривой равняется 1,
половина этой площади равняется 0,5)
QЦ1 QЦ
Рис. 2. Кривая распределения прочности целика.
По таблице значений функции Лапласа (приложение 2) находим, что значению Ф(t) = 0,49 соответствует значение t = 2,33.
Из кривой распределения прочности целика (рис. 4) выражаем t.
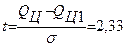 ,
,
| где | QЦ | - | среднее значение временного сопротивления целика сжатию, МПа; |
| QЦ1 | - | временное сопротивление целика сжатию при уровне риска разрушения целика Р = 1%, МПа; | |
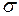
| - | среднее квадратичное отклонение (в данной задаче в МПа). |
Среднее квадратичное отклонение находится по формуле:
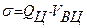 ,
,
| где | 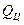
| - | среднее значение измеряемой величины (в нашем случае среднее значение временного сопротивления целика сжатию, МПа); |
| VВЦ | коэффициент вариации измеряемой величины (в данной задаче прочности целика). |
Следовательно, 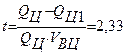
Из полученной формулы выражаем несущую способность целика QЦ1:
 , МПа
, МПа
Найдем коэффициент вариации прочности целика VВЦ.
По исследованиям Д.Ф. Коутса коэффициент вариации прочности целика VВЦ можно принимать в пределах 1,05 – 1,15 от коэффициента вариации прочности образцов VВО (%).
Принимаем 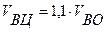 , %
, %
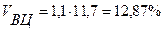
Найдем несущую способность целика QЦ1 при уровне риска его разрушения Р = 1%:
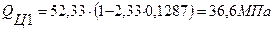
Задание для самостоятельного решения
Определить несущую способность целика цилиндрической формы диаметром 5 м и высотой 10 м по данным испытаний на сжатие образцов, изготовленных из материала целика. Результаты испытаний образцов на сжатие приведены в табл. 11.
Целик представлен крепким песчаником, слегка нарушенным одной системой несообщающихся трещин, расположенных на расстоянии 1,2 – 1,5 м друг от друга. Уровень риска разрушения целика принять 0,9%.
Таблица 5
| Число испытаний | Размеры образца | Объем V, см3 | Среднее значение временного сопротивления образца сжатию и коэффициент вариации по вариантам | ||||||
| диаметр d, см | высота h, см | 1 | 2 | 3 | |||||
| Q, МПа | VВО, % | Q, МПа | VВО, % | Q, МПа | VВО, % | ||||
| 3,0 | 6,0 | 42,39 | |||||||
| 3,5 | 7,0 | 67,31 | |||||||
| 4,0 | 8,0 | 100,48 | |||||||
| 4,5 | 9,0 | 143,07 | |||||||
| 5,0 | 10,0 | 196,25 | 112,5 | ||||||
| 5,5 | 11,0 | 261,21 | |||||||
| 6,0 | 12,0 | 339,12 | 13,0 | 108,7 | 10,0 | ||||
| Среднее | 11,7 | 11,3 | 11,6 |
Дата добавления: 2014-12-21; просмотров: 1326;
