Занимают одинаковые объемы.
При нормальных условиях (Т = Т0, р = р0) этот объем Vμ (молярный объем)равен:
Vμ = 22,41·10--3 м3/моль.
6.2. Закон Бойля-Мариотта
Для данной массы газа m при постоянной температуре Τ
произведение давления ρ на объем V есть величина постоянная:
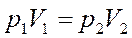 , или: , или: 
| Для данной массы газа при неизменной температуре (m = const, T = const). |
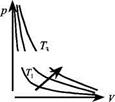 Кривая, изображающая зависимость между p и V, характеризующая свойства вещества при постоянной температуре, называется изотермой.
Кривая, изображающая зависимость между p и V, характеризующая свойства вещества при постоянной температуре, называется изотермой.
Изотермы — гиперболы, расположенные на графике тем выше, чем выше температура происходящего процесса.
6.3. Закон Дальтона.
Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.
|
 Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений p1,p2,...,pn входящих в нее газов:
Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений p1,p2,...,pn входящих в нее газов:
p = p1 + p2 + … + pn или pp = Σpi , где i =1…n.
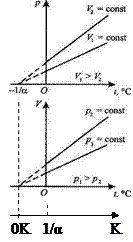
6.4. Закон Гей-Люссака.
|
объеме изменяется линейно с температурой tпо закону:
р = p0(1 + αt ) при V = const, т = const.
2) Объем Vданной массы т газа при постоянном
давлении изменяется линейно с температурой t:
V = V0( 1 + αt ) , при ρ = const; m = const,
где α = 1/273К-1, Vo и р0 — объем и давление при t = 0 0C.
Процесс,протекающий при постоянном давлении, называется изобарным.
На диаграмме в координатах (V,t) этот процесс изображается прямой, называемой изобарой.
Процесс,протекающий при постоянном объеме, называется изохорным.
На диаграмме в координатах (p,t) он изображается прямой, называемой изохорой.
Изобары и изохоры пересекают ось температуры в точке t = -1/α = -273° С. Если начало отсчета сместить в эту точку, то получим шкалу Кельвина (термодинамическую температуру):
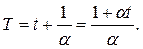 или
или 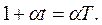
В термодинамической шкале температур закон Гей-Люссака:
V = V0(1 + αt) = V0αT, p = p0(1 + αt) = p0 αT
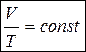 |
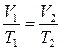 Откуда: или при p = const ; m = const.
Откуда: или при p = const ; m = const.
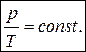 | |||
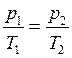 | |||
или при V = const ; m = const. (з-н Шарля),
где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре.
Уравнение Клайперона-Менделеева
(для Пр.зан)
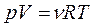 ,
,
где R = 8,31 Дж/К – молярная газовая постоянная.
9. Уравнение состояния идеального газа
(уравнение Клайперона – Менделеева)
Уравнением состояния термодинамической системы называется уравнение, которое связывает давление р, объем V и температуру Τ термодинамической системы, находящейся в состоянии термодинамического равновесия:
f(p,V,T) = 0,
где каждая из переменных является функцией двух других.
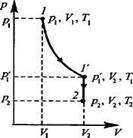 Пусть некоторая масса газа занимает объем V1,
Пусть некоторая масса газа занимает объем V1,
имеет давление р1и находится при температуре Τ1. Эта же масса газа в другом произвольном состоянии характеризуется параметрами p2,V2,T2. Переход из состояния 1 в состояние 2 осуществляется последовательно изотермическим (1-1') и изохорным (1'-2) процессами.
По законам Бойля-Мариотта и Гей-Люссака.
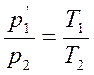 | |||
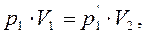 | |||
Исключая р1’, получим уравнение состояния идеального газа:
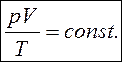 | |||
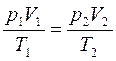 | |||
или
По закону Авогадро, при одинаковых pи Τмоли всех газов занимают одинаковый молярный объем Vμ.
Уравнение состояния для 1моля идеального газа:
ρVμ = RT,
где R = 8,31 Дж/(моль·К) — называется универсальной газовой постоянной.
Объем газа массы отсюда
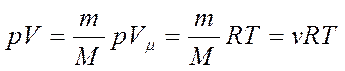 | |||
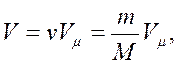 | |||
Макроскопические параметры – параметры, характеризующие состояние системы: Температура, давление, объем, и т.д. (например, электрическое сопротивление).
Уравнение Менделеева-Клапейрона — уравнение состояния для массы т идеального газа:
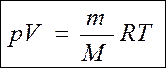 | |||||
| |||||
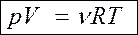 | |||||
Если использовать постоянную Больцмана:
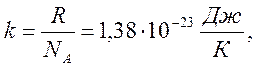 |
( 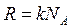 ),
),
то уравнение состояния для одного моля вещества примет вид:
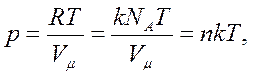 | |||
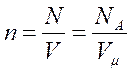 | |||
где n - концентрация молекул – число молекул в единице объема.
Tаким образом:
1) давление идеального газа при данной температуре прямо
пропорционально концентрации его молекул,
2) при одинаковых температуре и давлении все газы содержат в единице
объема одинаковое число молекул.
Число молекул, содержащихся в 1м3 газа при нормальных условиях, называется числом Лошмидта:
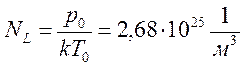 |
10. Основное уравнение молекулярно-кинетической теории идеальных газов
Пусть в сосуде объемом V находится идеальный газ массой m, cостоящий из N молекул массой m0, движущихся с одинаковыми скоростями v. Концентрация молекул в газе по определению n = N/ V.
Если при соударениях со стенками за время Δt элементарной площадке ΔS стенки сосуда передается импульс ΔР, то давление газа, оказываемое имна стенку сосуда
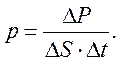 |
При каждом соударении молекула, движущаяся перпендикулярно стенке, передает ей импульс 2m0v. В среднем по направлению к стенке движется 1/6 часть всех молекул. (Если рассмотреть три взаимно перпендикулярные оси, то в среднем только 1/3 молекул движется вдоль одной из осей и только половина из них 1/2(1/3) вдоль данного направления.)
Поэтому, за время Δt площадки ΔS достигнут
N = 1/6·n·ΔS·v·Δt
молекул и передадут ей импульс
ΔΡ =1/3·n·m0·v2·ΔSΔt.
Давление, оказываемое газом на стенку сосуда: ρ = 1/3nm0v2.
Если газ в объеме V содержит N молекул, движущихся со скоростями
vl,v2,...,vN,
то целесообразно рассматривать среднюю квадратичную скорость, которая
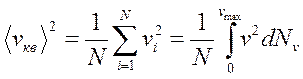 |
определяется как и
характеризует всю совокупность молекул газа.
Основное уравнение молекулярно-кинетической теории идеальных газов:
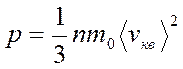 |
Другие варианты записи основного уравнения молекулярно-кинетической теории идеальных газов с учетом соотношений :
n = N/V и m = Nm0:
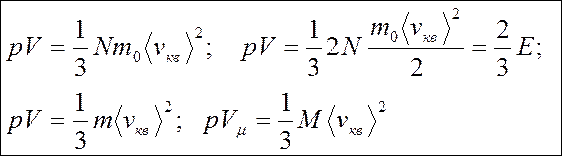
Здесь Ε — суммарная кинетическая энергия поступательного движения всех молекул газа, Vµ - молярный объем, M — молярная масса.
Используя уравнение Клапейрона - Менделеева, получим
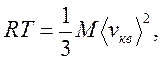 |
откуда находим среднюю квадратичную скорость молекул идеального газа:
11 .Средняя квадратичная скорость молекул идеального газа:
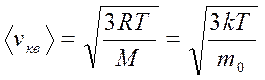
где использовано M = m0 NAи k = R/NA .
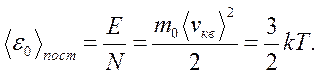 Средняя кинетическая энергия поступательного движения одной молекулы идеального газа:
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа:
Отсюда следует, что (εο) = 0 при Т = 0 К— прекращается движение молекул газа.
Молекулярно-кинетическое толкование температуры:
термодинамическая температура — есть мера средней кинетической энергии поступательного движения молекул газа.
12. Закон Максвелла о распределении молекул идеального газа
по скоростям
В газе, находящемся в состоянии равновесия при данной температуре, устанавливается некоторое стационарное, не меняющееся со временем, распределение молекул по скоростям.
Это распределение описывается функцией f(v), называемой функцией распределения молекул по скоростям, которая определяет относительное число молекул, скорости которых лежат в интервале от υ до υ + dv,
 т.е.
т.е. 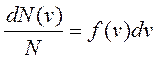
Закон Максвелла:
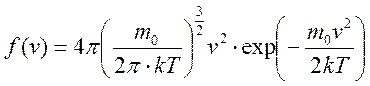 |
Эта функция удовлетворяет условию нормировки:
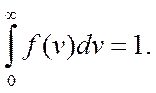 |
13. Наиболее вероятная скорость молекул идеального газа
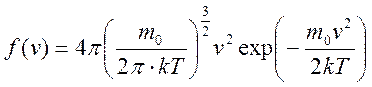 Из прошлой лекции, согласно закону Максвеллаплотность распределения молекул по скоростям:
Из прошлой лекции, согласно закону Максвеллаплотность распределения молекул по скоростям:
 |
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной споростью υΒ.
Приравняв 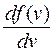 нулю, получаем:
нулю, получаем: 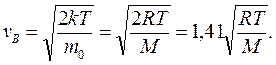
14. Средняя скорость молекулы газа:
(средняя арифметическая скорость)
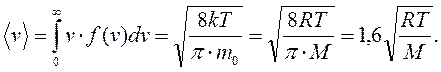 |
15. Средняя квадратичная скорость молекул идеального газа (Л2):
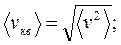
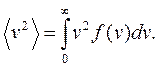
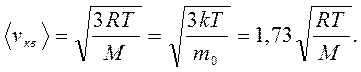 |
Дата добавления: 2014-12-20; просмотров: 1081;
