Обработка результатов многократных измерений.
Обработка результатов многократных измерений, согласно ГОСТ 8.207 «ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения», заключается в нахождении результата измерения ФВ и доверительного интервала, в котором находится ее истинное значение.
Исходной информацией для обработки является ряд из n (n > 4) результатов единичных измерений x1, x2 …,xn, из которых исключены известные систематические погрешности. Число измерений зависит от требований к точности получаемого результата и от реальной возможности выполнения повторных измерений.[14]
Последовательность обработки результатов многократных измерений включает в себя следующие основные этапы:
1) Исключение из результатов измерений известных систематических погрешностей;
2) Вычисление среднего арифметического значения измеряемой величины из n единичных результатов по формуле:
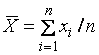 ( 1)
( 1)
3) Вычисление средней квадратической погрешности (СКО) единичных измерений в ряду 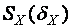 измерений по формуле:
измерений по формуле:
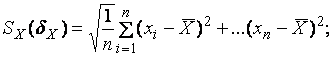 (2)
(2)
4) Исключение промахов (грубых погрешностей измерений);
5) Вычисление средней квадратической погрешности результата измерений среднего арифметического
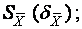 (3)
(3)
6) Вычисление доверительных границ случайной погрешности результата измерений 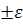 по формулам (4) и (5);
по формулам (4) и (5);
7) Вычисление доверительных границ погрешности результата измерений ±∆;
8) Представление результата измерений в виде 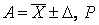 QUOTE A=x±Δ,
QUOTE A=x±Δ, 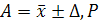 P , где P – доверительная вероятность.
P , где P – доверительная вероятность.
При заданном значении доверительной вероятности P и числе единичных измерений n определяют коэффициенты Стьюдента tp (табл. 3.2).
Таблица 3.2. - Значения коэффициента Стьюдента tp (ГОСТ 8.207-76)
| р | n- число единичных измерений | |||||||||
| 0,95 | 12,706 | 0,95 | 12,706 | 0,95 | 12,706 | 0,95 | 12,706 | 0,95 | 12,706 | 0,95 |
| 0,99 | 63,657 | 0,99 | 63,657 | 0,99 | 63,657 | 0,99 | 63,657 | 0,99 | 63,657 | 0,99 |
Доверительные границы случайной погрешности результата измерений ε определяют по следующей формуле:
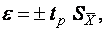 (4)
(4)
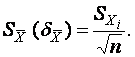 (5)
(5)
Пример обработки измерений, выполненных дифманометром:
При обработке уже имеющихся результатов измерений для исключения грубых погрешностей поступаем следующим образом:
1) Вычисляем среднее арифметическое nрезультатов наблюдений 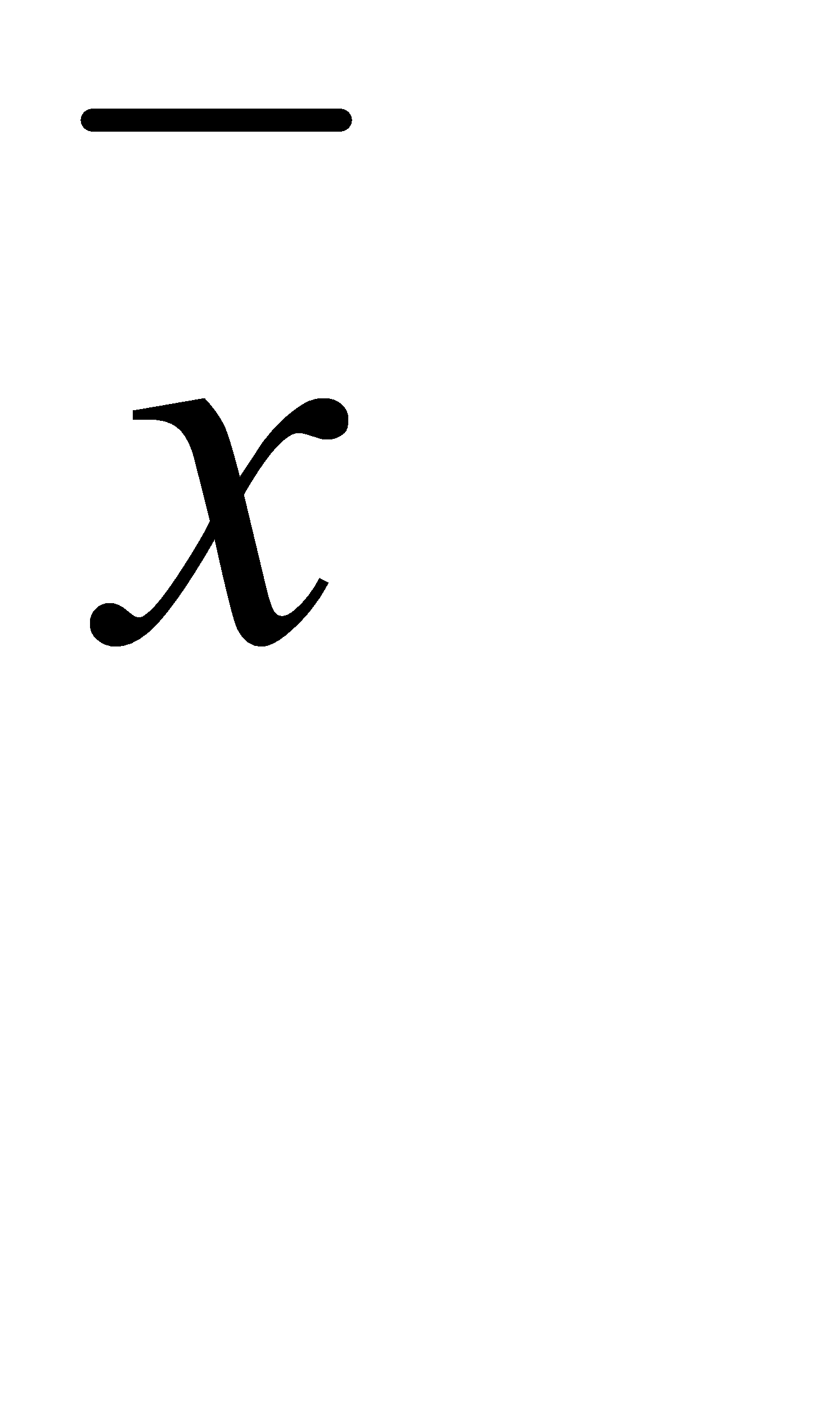 по формуле (1), данные измерений представлены в таблице 3.3:
по формуле (1), данные измерений представлены в таблице 3.3:
Таблица 3.3. - Результаты измерений.
| № | Показания, полученные в результате измерений. | Показания эталонного прибора |
| 1. | 24,9 кПа | 25,00 кПа |
| 2. | 25,1 кПа | 25,1 кПа |
| 3. | 25,00 кПа | 25,00 кПа |
| 4. | 25,2 кПа | 25,00 кПа |
| 5. | 24, 9 кПа | 25,00 кПа |
| 6. | 25,2 кПа | 25,00 кПа |
| 7. | 25,00 кПа | 25,00 кПа |
| 8. | 25,3 кПа | 25,00 кПа |
| 9. | 25,2 кПа | 25,00 кПа |
| 10. | 25,37 кПа | 25,00 кПа |
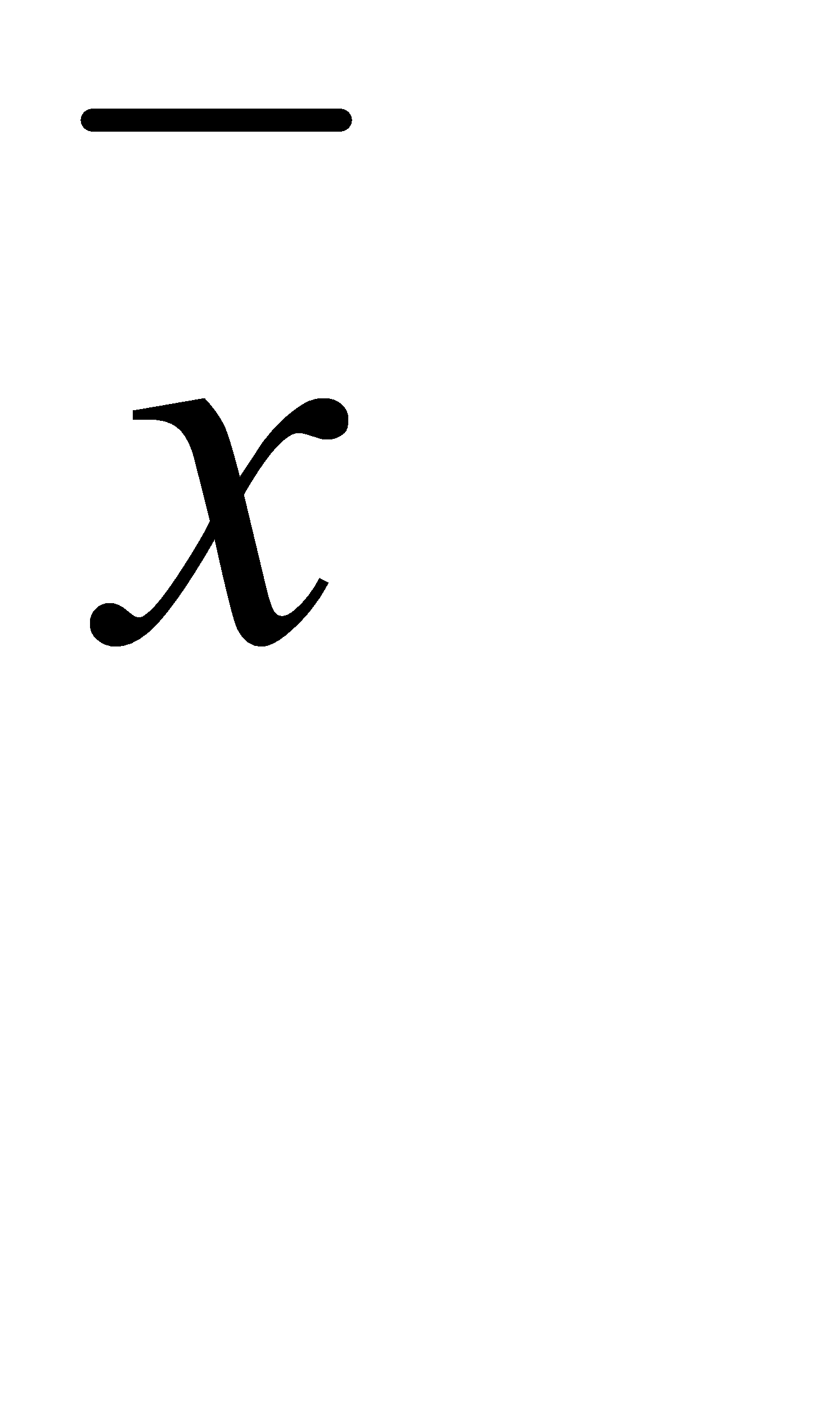 =
= 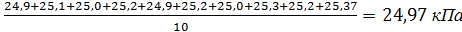
2) Вычисляем оценку среднего квадратического отклонения S результата измерений (2):
S = 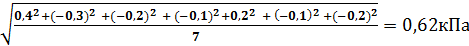
3) Определяем наличие (отсутствие)предполагаемого промаха хпот 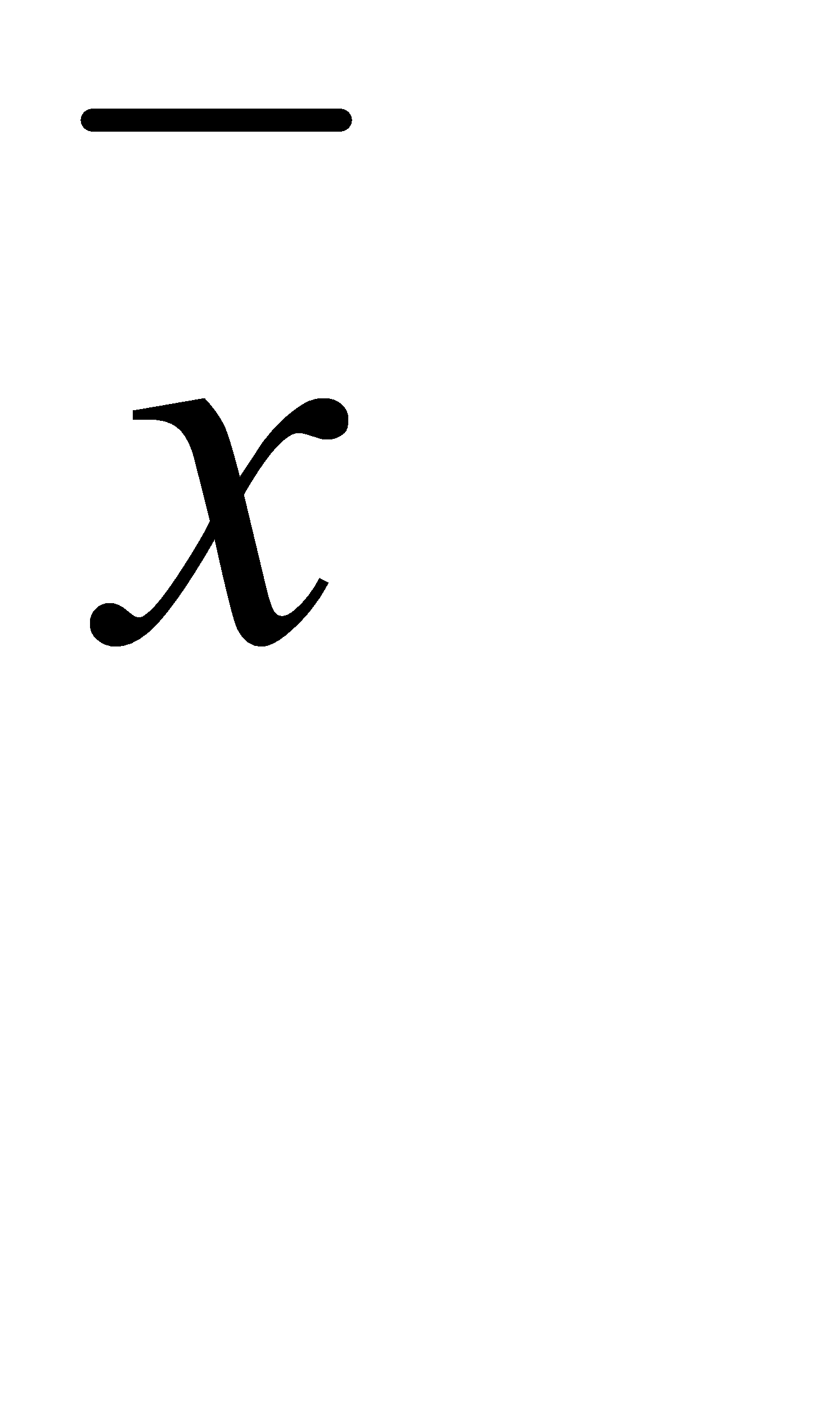 .Применяем критерий Романовского при n = 10. (табл.3.3)
.Применяем критерий Романовского при n = 10. (табл.3.3)
Таблица 3.4. – Критерии Романовского по ГОСТ 8.207-76
| P | N | |||||||||||
| 0,95 | 1,414 | 1,710 | 1,917 | 2,067 | 2,182 | 2,273 | 2,414 | 2,519 | 2,602 | 2,670 | 2,78 | |
| 0,99^ | 1,414 | 1,728 | 1,972 | 2,161 | 2,431 | 2,532 | 2,616 | 2,753 | 2,855 | 2.946 | 3,08 |
При этом вычисляют отношение:
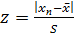
При n=10 получаем zт =2,414 соответственно z при этом вычисляем как:
Z = 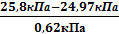 = 1,34
= 1,34
Поскольку z = 1,34 < 2,414, то, следовательно, значение во второй выборке 25,8 не является промахом.
Так как промахи измерений отсутствуют, то за результат измерения принимают среднее арифметическое результатов наблюдений.
При симметричной доверительной погрешности результаты представляют в форме Xср. ± ΔX, Р (Р– доверительная вероятность). Числовое значение результата измерения должно оканчиваться цифрой 1-го же разряда, что и значение погрешности.
Представляем результат измерения в виде X = 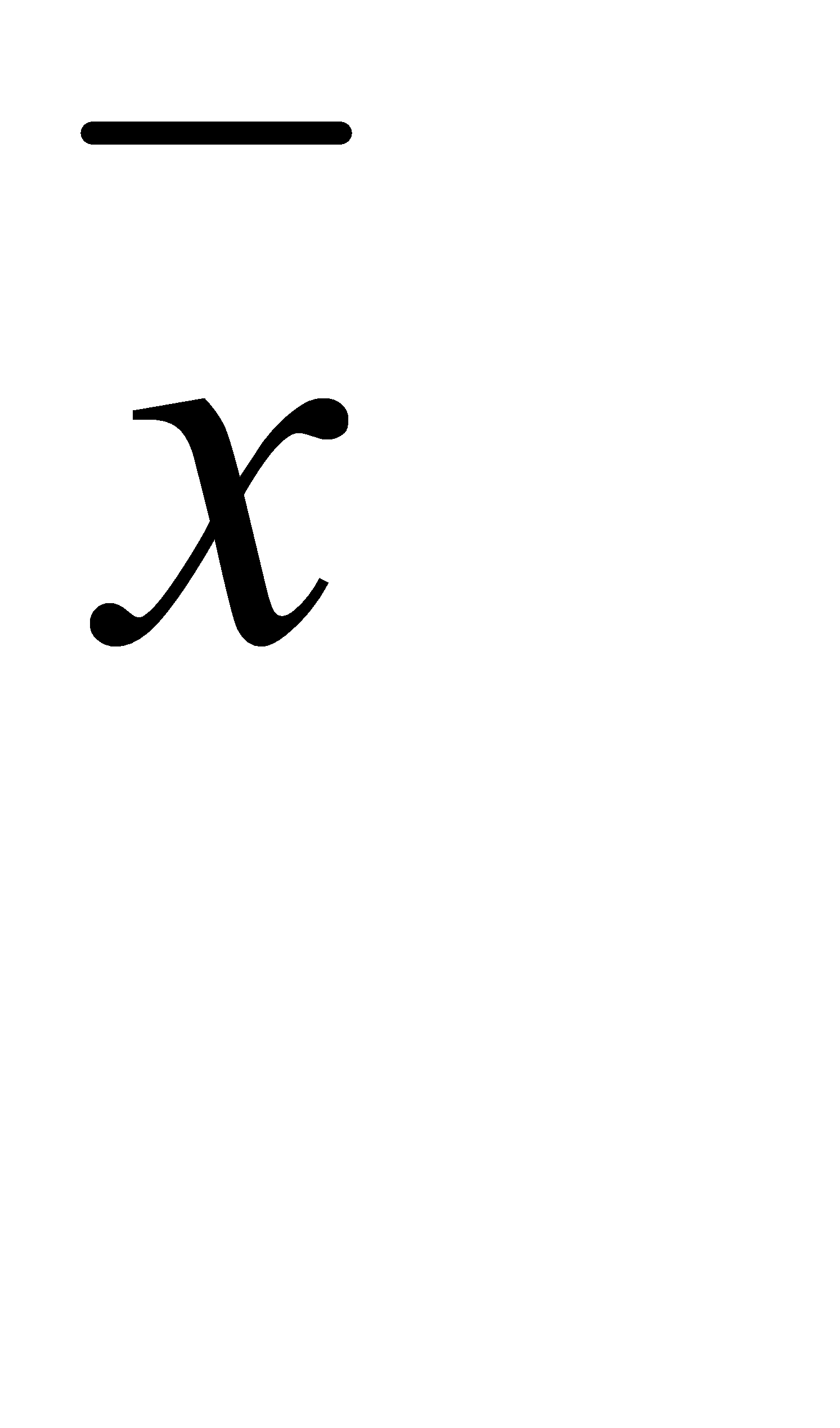 ± (Δx)Σ , Р
± (Δx)Σ , Р
В данном случае X = Xср. ± ΔX = 24,97 ± 1,34 кПа, 0,95. [7]
Результаты измерений и вычисления абсолютной погрешности представлены в таблице 3.5.:
Таблица 3.5. - Результаты абсолютной погрешности.
| № | Показания, полученные в результате измерений. | Показания образцового прибора | Абсолютная погрешность |
| 1. | 24,9 кПа | 25,00 кПа | 0,1 кПа |
| 2. | 25,1 кПа | 25,1 кПа | 0,1 к Па |
| 3. | 25,00 кПа | 25,00 кПа | 0,000 кПа |
| 4. | 25,2 кПа | 25,00 кПа | 0,2 кПа |
| 5. | 24, 9 кПа | 25,00 кПа | 0,1 кПа |
| 6. | 25,2 кПа | 25,00 кПа | 0,2 кПа |
| 7. | 25,00 кПа | 25,00 кПа | 0,00 кПа |
| 8. | 25,3 кПа | 25,00 кПа | 0,3 кПа |
| 9. | 25,2 кПа | 25,00 кПа | 0,2 кПа |
| 10. | 25,37 кПа | 25,00 кПа | 0,370 кПа |
ΔX= X0 - X
1. 25,00 кПа – 24,9 кПа = 0,1 кПа
2. 25,00 кПа – 25,1 кПа = 0,1 кПа
3. 25,00 кПа – 25,00 кПа = 0,00 кПа
4. 25,00 кПа – 25,2 кПа = 0,2 кПа
5. 25,00 кПа – 24,9 кПа = 0,1кПа
6. 25,00 кПа – 25,02 кПа = 0,2 кПа
7. 25,00 кПа - 25,00 кПа = 0,00 кПа
8. 25,00 кПа – 25,3кПа = 0,3 кПа
9. 25,00 кПа – 25,2 кПа – 0,2 кПа
10. 25,00 кПа – 25,370 кПа = 0,370 кПа
При поверке было выявлено, что погрешность поверяемого прибора не превышает погрешности образцового прибора (1,5% от измеряемой величины (см. Табл. 2.2), в данном случае 0,375 кПа), из чего можно сделать вывод, что поверяемый прибор пригоден для использования.
Дата добавления: 2014-12-20; просмотров: 4314;
