Продовження таблиці 4.2.1
| ПРОИЗВЕД(число1; число2; ...) Результат: добуток аргументів | Математические |
| СРЗНАЧ(число1; число2; ...) Результат: середнє арифметичне значення аргументів | Статистические |
| СУММ(число1; число2; ...) Результат: сума аргументів | Математические |
| СУММЕСЛИ (диапазон; “критерий”; диапазон_суммирования) Результат: сума клітинок, що задовольняють заданому критерію | Математические |
| СУММПРОИЗВ(массив1; массив2) Результат: сума добутків відповідних елементів масивів | Математические |
| СЧЕТ(значение1; значение2; ...) Результат: кількість чисел у списку аргументів | Статистические |
| СЧЕТЕСЛИ(диапазон; “критерий”) Результат: кількість клітинок діапазону, що задовольняють заданому критерію | Статистические |
| ТРАНСП(массив) Результат: транспонована матриця; треба вводити як формулу масиву | Ссылки и массивы |
Далі наведені приклади використання функцій електронної таблиці.
Приклад 1. Функції СУММЕСЛИ, СЧЕТЕСЛИ. Особливості використання цих функцій розглянемо на прикладі електронної таблиці, представленої на рис. 3.
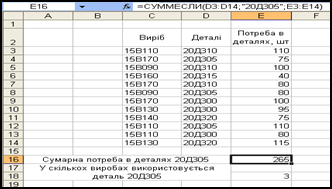
Рис. 3 – Розрахунки за функціями СУММЕСЛИ,СЧЕТЕСЛИ
Нехай, наприклад, треба розрахувати сумарну потребу в деталях 20Д305. Для цього спочатку активізують кнопку Вставка функции,у переліку знаходять функцію СУММЕСЛИ. Її аргумент Диапазонмістить значення діапазону комірок з назвами деталей, серед яких відшукуються ті, що задовольняють умову, поставлену в аргументі Критерий.Цей аргумент може містити число, умову, текст, адресу комірки, що містить потрібну назву (наприклад, 45, >1, "20Д305", A3).
Аргумент Диапазон_суммированиямістить діапазон тих клітинок, в якому відбувається підсумовування; при цьому обробляються тільки ті записи, значення яких задовольняють поставлену умову. Якщо Диапазон_суммированияпропущений, то обробляються комірки, адреси яких задано в аргументі Диапазон.
З урахуванням наведених пояснень для обчислення сумарної потреби в деталях типу 20Д305 у клітинку Е16 вводимо таку формулу
=СУММЕСЛИ(D3;D14;”20Д305”;E3:E14)
і отримуємо в результаті 265.
Функція СЧЕТЕСЛИ розраховує кількість заповнених комірок у діапазоні, які задовольняють поставлену умову. Якщо, наприклад, треба розрахувати, у скількох виробах використовується деталь 20Д305, то у клітинку E18 вводимо таку формулу
=СЧЕТЕСЛИ(D3:D14;"20Д305")
і отримуємо в результаті 3.
Приклад 2. Функція ЕСЛИ. Функція ЕСЛИ використовується для перевірки умови стосовно значень та формул і повертає одне розраховане значення, якщо задана умова після розрахунку дає значення ІСТИНА, й інші розраховані значення, якщо значення умови після розрахунку буде ХИБНІСТЬ. Аргументами функції можуть бути до семи вбудованих функцій в разі складних перевірок.
Нехай треба розрахувати значення функції такого вигляду:

для, наприклад, двох значень аргументу х = 2,1 і х = -1,3.
Спочатку в діапазон клітинок А2:А3 (рис.4) заносять значення х й активізують клітинку для розрахунку першого значення у (клітинка В2).
Далі активізують кнопку Вставка функции,знаходять функцію ЕСЛИ й активізують кнопку ОК.
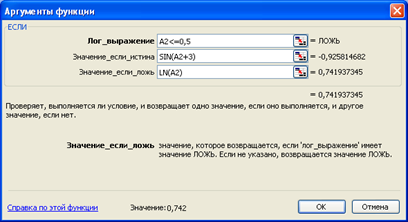
Рис. 4 - Введення аргументів функції ЕСЛИ
В аргументі Лог_выражение(рис. 4) створюють умову для першого рівняння (х≤0,5), причому х в Excel — це адреса клітинки, що містить значення х. Умова матиме вигляд А2<=0,5.
Аргумент Значение_если_истинамістить розрахунок першого рівняння, якщо умова аргументу Логическое выражениемає значення ІСТИНА. Аргумент Значение_если_ложьмістить розрахунок другого рівняння, якщо умова аргументу Логическое выражениемає значення ХИБНІСТЬ. Після натискування кнопки ОК створена формула заноситься у клітинку В2 і за цією формулою здійснюється обчислення для першого значення х.

Рис.5- Розрахунок за функцією ЕСЛИ
Далі її копіюють для другого значення у, і в результаті електронна таблиця набуває вигляду, показаного на рис. 5.
Приклад 3. Обчисленняз матрицами. Для роботи з матрицями використовують різні функції (табл. 1). Матриці можна перемножувати між собою, множити на вектор, транспонувати, створювати обернені матриці тощо.
Розрахунки з матрицями розглянемо на прикладі розв’язування системи лінійних рівнянь, заданої в матричної формі А×Х=С,де А –матриця системи, С – вектор вільних членів, Х – вектор розв’язку (корені) системи. Нехай
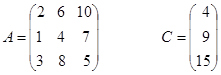
Якщо визначник матриці А не дорівнює нулю, то розв’язок системи лінійних рівняньА×Х=С знаходиться за формулою Х=А-1×С, де А-1 – обернена матриця А.
Спочатку створюють матрицю, А, наприклад, у діапазоні клітинок А2:С4, а вектора С –у діапазоні клітинок Е2:Е4 (рис. 6). Після цього над елементами матриці А і вектора С можна виконувати дії, що потрібні для розв’язування системи рівнянь.
Обчислення визначника матриці. Для обчислення визначника матриці застосовується функція МОПРЕД(массив), де массив – діапазон клітинок, в який записана матриця. У прикладі, що розглядається, для обчислення визначника матриці А у клітинку Е6 записана формула =МОПРЕД(А2:С4). Визначник не дорівнює нулю (рис. 6), таким чином, система має розв’язок.
Створення оберненої матриці.Треба створити обернену матрицю А-1 з елементів матриці А. Такі обчислення виконуються за формулою масиву. Для цього виділяють діапазон комірок (А9:С11), де буде створюватися нова матриця, активізують кнопку Вставка функции,вибирають функцію МОБР, і заносять відповідні значення елементів матриці А, в результаті отримують формулу =МОБР(А2:С4). Після цього встановлюють курсор на рядок формул та натискують на клавіші Ctrl+Shift+Enter.
Множення матриці на вектор.Нехай, наприклад, треба помножити матрицю на вектор. Для цього використовують функцію МУМНОЖ (Массив1; Массив2),де Массив1, Массив2— це масиви, які перемножуються. Кількість стовпців аргументу Массив1має бути такою, як і кількість рядків аргументу Массив2.Результатом множення матриць є масив з такою самою кількістю рядків, що й масив1, і з такою самою кількістю стовпців, що й масив2. Множення матриці на вектор виконується за формулою масиву.
Для розв’язування системи рівнянь матрицю А-1 требапомножитина векторС.Результатом будевектор розв’язку Х,для розміщення якого потрібні три клітинки, наприклад, Е9:Е11. Їх треба виділити, активізувати кнопку Вставка функции,вибрати функцію МУМНОЖ і занести відповідні значення діапазонів матриці А-1 та вектора С (рис. 4.2.9).
Після цього встановлюють курсор на рядок формул, натискують на клавіші Ctrl+Shift+Enterй одержують формулу МУМНОЖ(А9:С11;Е2:Е4).
Для перевірки розв’язку треба матрицю системи Апомножимо на знайдений вектор Х.Отриманий вектор повинен збігатися з вектором С.
Функції, що застосовувалися при розв’язуванні системи лінійних рівнянь, та отриманий розв’язок представлені відповідно на рис. 6 і 7.
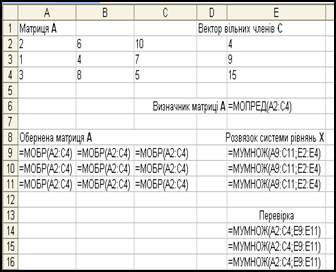
Рис. 6 - Функції, що застосовуються для розв’язання системи лінійних рівнянь
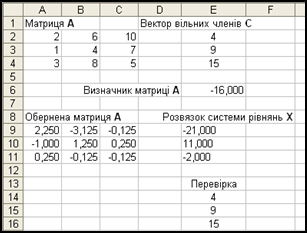
Рис.7- Розраховані значення коренів системи лінійних рівнянь
Дата добавления: 2014-12-20; просмотров: 1935;
