Концепции и методологические принципы квантовой механики. Понятие квантового микросостояния

Крушение классической физики и как следствие классического естествознания связано прежде всего со знаменитым немецким физиком-теоретиком Максом Планком, который связал хаотичность электромагнитного (светового) излучения атомных осцилляторов с их дискретностью и выдвинул идею квантового излучения энергии каждым осциллятором пропорционально частоте колебаний. Планк ввел коэффициент пропорциональности, новую фундаментальную константу 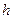, имеющую размерность действия (энергия, умноженная на время), получившую название постоянной Планка:

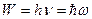, где .

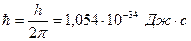Квантовая гипотеза М. Планка сняла проблему «ультрафиолетовой катастрофы» теплового излучения, согласно которой, исходя из классических представлений о тепловом излучении, энергия излучения любого тела при любой температуре должна быть абсурдно бесконечной. А. Эйнштейн первым подхватил идею М. Планка, предположив, что электромагнитные волны не только излучаются, но и поглощаются квантами. Эта гипотеза позволила ему на основе формулы Планка и закона сохранения энергии получить в 1905 г. уравнение для внешнего фотоэффекта, подтвержденное в дальнейшем экспериментально рядом ученых и позволившее экспериментально определить постоянную Планка. Когда же было экспериментально продемонстрировано, что и процесс распространения света имеет квантовый характер (опыты В. Боте. Г. Гейгера, А. Комптона), стало ясно, что свет имеет двойственную корпускулярно-волновую природу. Так, свет при интерференции, дифракции, поляризации проявляет чисто волновые свойства, а при излучении нагретых тел, люминесценции, внешнем фотоэффекте, фотопроводимости – чисто корпускулярные свойства, т.е. как поток «частиц» (квантов), которые назвали фотонами.

Боровская теория водородоподобного атома, в основу которой Н. Бор в 1913 г. закладывает идею о квантовании величины действия при движении электрона по круговой орбите («планетарная модель атома Резерфорда-Бора»), подкрепляла возникший корпускулярно-волновой дуализм света.

И совершенно «безумная», но «революционная» в «драме идей» становления квантовой механики гипотеза была выдвинута Луи де Бройлем о том, что с двигающимся электроном связана некая волна, длина волны 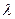которой равна 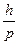, где 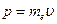- импульс электрона. Он применил эту идею к интерпретации стационарных орбит боровской модели атома. Он считал, что в длине такой орбиты укладывается целое число длин волн электрона, и тогда волны электрона находятся в фазе сами с собой и не разрушаются собственной интерференцией. В 1924 г. де Бройль изложил эту идею в своей диссертации «Исследования по квантовой теории», которую поддержал А. Эйнштейн. Последний рекомендовал эту работу Эрвину Шредингеру, который на основе этой идеи создал одно из основных направлений квантовой механики – волновую механику.

В 1927 г. эксперименты Дэвиссона и Джермера подтвердили «безумную» идею де Бройля в опытах по наблюдению дифракции электронов от кристалла никеля. В том же 1927 г. Дж. П. Томсон наблюдал дифракцию быстрых электронов на очень тонкой металлической фольге, изготовленной из поликристаллического материала с хаотическим расположением кристаллических осей.

В настоящее время корпускулярно-волновой дуализм распространяется на все элементарные частицы, а следовательно на все исходные принципы квантовой механики и их применения к материи, движению и фундаментальным взаимодействиям.

Эти исходные принципы квантовой механики в сжатой форме сформулировал Р. Фейнман в своих знаменитых лекциях по физике на основе рассмотрения прохождения щели электронами(см. рис. 5.1). Мы объединили в одном рисунке интерференцию электронных волн (б) со световым наблюдением за электронами (в).

Теперь попробуем в сжатой форме прокомментировать результаты эксперимента на нашем электронном приборе. При этом мы изложим, следуя Р. Фейнмана, результаты в такой форме, чтобы они имели силу для всего класса аналогичных экспериментов. Для этого сформулируем определение идеального эксперимента: «Идеальным называется такой эксперимент, в котором все начальные и конечные условия полностью определены».

Теперь об общих выводах, которые приведем в краткой форме:

1. Вероятность некоего события в идеальном эксперименте, например, прохождения электронов через отверстие 1 или через отверстие 2 и их измерения с помощью щелчков на детекторе, равняется квадрату абсолютного значения комплексного числа 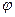, именуемого амплитудой вероятности.

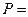вероятность, 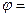амплитуда вероятности, 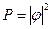и тогда 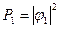и .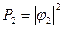

2. Если событие в эксперименте может осуществляться несколькими взаимно исключающими способами, т.е. когда, например, открыты оба отверстия (щели) и мы не фиксируем через какую щель проходит тот или иной электрон, то амплитуда вероятности для каждого отдельного события равняется сумме амплитуд вероятности для каждого отдельного способа. При этом «имеет место интерференция» (рис. 5.1, (б)).

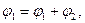
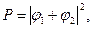а .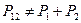

3. Если проводится эксперимент, дающий возможность определить, какой из этих двух взаимно исключающих способов осуществляется в действительности (в нашем случае контролем прохождения электронов с помощью сильного источника света), то вероятность события равна сумме вероятностей для каждого отдельного способа. Интерференция отсутствует.

.

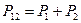Основные идеи, принципы и законы квантово-полевой картины мира в определённой степени отражены в предыдущей лекции №3 (см. схему 21).

Мы их концептуальную основу отразим на основе выделения основополагающих концепций и методологических принципов квантовой механики (см. схему 33).