Коло синусоїдного струму з ємністю.
Коло, яке стосовно джерела синусоїдної напруги u = UСmsin(wt + yu) має виключно ємнісний характер навантаження можна надати у вигляді конденсатора ємністю С, що підключений до джерела дуже короткими провідниками (рис. 2.14, а).
Струм у такому колі являє собою рух зарядів q до обкладинок конденсатора і може бути описаний диференційним рівнянням –
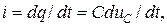
де uС – спад напруги на конденсаторі.

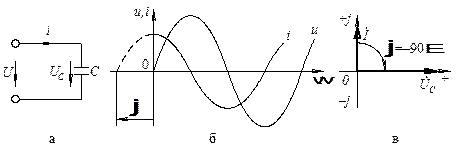 Враховуючи, що внутрішній опір з’єднувальних проводів дуже малий, і, отже, згідно з другим законом Кірхгофа –
Враховуючи, що внутрішній опір з’єднувальних проводів дуже малий, і, отже, згідно з другим законом Кірхгофа –
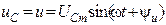 ,
,
рішення диференційного рівняння буде мати вигляд:

Розділивши обидві частини виразу амплітудного значення струму ємності (Im = wCUm) на 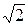 , одержимо рівняння розрахунку діючого струму кола – закон Ома для кола (ділянки кола) з ємністю:
, одержимо рівняння розрахунку діючого струму кола – закон Ома для кола (ділянки кола) з ємністю:
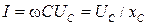 ,
,
де xC = 1/(wC) = 1/(2pfC) – реактивний опір ємності, або ємнісний опір, який відображає вплив ємності на величину діючого струму.
Для кола (ділянки кола) з ємністю закон Ома у комплексній формі буде:

З викладеного випливає, що струм у колі з ємністю, подібно до прикладеної напруги, змінюється за синусоїдним законом. Так як синусоїди напруги і струму кола з ємністю мають початкові фази, відповідно: yu та yi = yu + p/2, то кут зсуву фаз між ними буде:
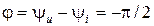 .
.
В загальному випадку суміщені часова та векторна діаграми струму і напруги кола (ділянки кола) з ємністю мають вигляд, як на рис. 2.14, б та рис. 2.14, в. При побудові цих діаграм прийнято, що yu = 0°.
Миттєву потужність кола з ємністю визначають так:
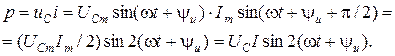
З аналізу рівняння розрахунку p випливає, що миттєва потужність кола (ділянки кола) з ємністю змінюється за синусоїдою частота якої у 2 рази більша, ніж у синусоїд струму або напруги.

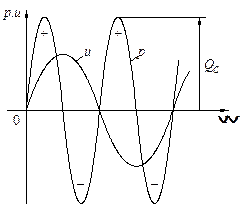
З графіка p = f(t)(рис. 2.15) видно, що протягом першої чверті періоду синусоїди напруги, ємність накопичує енергію (WC = CU2Cm/2) з мережі (конденсатор заряджається) – іде процес перетворення енергії змінного струму в енергію електричного поля. У другу чверть періоду, ємність розряджається – віддає у мережу накопичену раніше енергію. Так відбувається безперервний періодичний процес обміну енергії між ємністю і мережею. Цей обмін відбувається без втрат енергії і тому середнє значення потужності кола (ділянки кола) з ємністю за період буде –
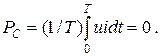
Потужність, яка без втрат коливається між джерелом і ємністю називають реактивною ємнісною потужністю QC, вар (вольт ампер реактивний). Її визначають за формулою:
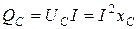 ,
,
Дата добавления: 2017-03-29; просмотров: 440;
