Макроскопические и микроскопические системы. Постулат равновероятности. Эргодическая гипотеза. Статистический вес. Флуктуации.

Системой называется совокупность физических объектов исследования, заключенных в конечной области пространства. Граница системы может быть как материальной (например стенка сосуда), так и воображаемой, проведенной в пространстве мысленно. Она может быть неподвижной или движущейся. Граница может быть проницаемой или непроницаемой для вещества, через нее либо невозможен, либо возможен транспорт энергии, причем в последнем случае она классифицируется по формам энергии, которые через нее могут транспортироваться.

Система характеризуется не только особенностями своей границы, но и физическими или химическими свойствами вещества, находящегося в занимаемой системой области пространства. Первая система, с которой начинается рассмотрение идеальный газ (точечные частицы конечной массы, столкновения между которыми происходят по законам абсолютно упругого удара шаров, силы взаимодействия на конечном расстоянии отсутствуют).

Если система изолирована, т.е. не обменивается энергией и веществом с окружающей средой, то рано или поздно она придет в стояние равновесия. ИГ в таком состоянии можно описать в помощью Р,V, Т.

Состояние газа, характеризуемое его давлением, температурой и объемом, называется макроскопическим.

Состояние газа, характеризуемое положениями и скоростями всех его частиц, называется микроскопическим. Если число частиц n ( 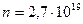в 1см³ при н.у.) то микроскопическое состояние газа характеризуется 6п числами (микропараметрами): 3п координатами 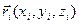всех частиц и 3п проекциями их скоростей 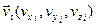. Все эти числа следует рассматривать как случайные величины.

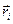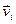В равновесном состоянии Р,V, Т – фиксированные величины, а вот и могут меняться. Возьмем очень большое число 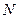совершенно одинаковых сосудов, каждый из которых имеет объем 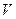. В каждом из сосудов находится одинаковое число n одинаковых частиц.

Сосуд с заключенными в нем частицами называется статистической системой.

Совокупность одинаковых статистических систем называется статистическим ансамблем.

Микроканонический ансамбль состоит из одинаковых изолированных систем с одинаковой энергией. Кроме микроканонических ансамблей в статистической физике рассматриваются также канонические и некоторые другие ансамбли.

Ø Допустим частицы, входящие в систему микроканонического ансамбля, считаются пронумерованными, пронумерованы также и ячейки, в которых могут находиться частицы.

Ø Известно, что атомы и молекулы имеют определенные размеры. Их диаметр имеет порядок 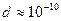м. Каждая молекула или атом занимает объем порядка 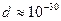м³, таким образом, в 1 м³ имеется всего 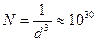ячеек. С другой стороны в 1 м³ воздуха при нормальных условиях находится 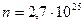частиц. Это означает, что в типичных условиях одна частица приходится на 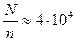ячеек.

Ø В некоторый момент времени некоторая частица находится в различных системах ансамбля в различных ячейках. Если ансамбль содержит очень большое число систем 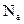, то число систем, в которых рассматриваемая частица окажется в ячейке 1, равна числу систем, в которых она оказалась в ячейке 2. Для данной частицы все возможные положения равновероятны. Микросостояние характеризуется положением всех 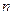частиц, входящих в систему, т.е. конкретным распределением этих частиц по ячейкам, на которые разбит объем.

Ø Поскольку все ячейки для каждой из частиц равновозможны, логично заключить, что все распределения частиц по ячейкам также равновозможны. А это означает, что все микросостояния равновероятны.

Одно и тоже макроскопическое состояние осуществляется в большом числе систем ансамбля, находящихся в различных микроскопических состояниях. Следовательно, данное макросостояние характеризуется большим числом микросостояний.

В основе всей статистической физики лежат не доказанные в общем случае постулат равновероятности и эргодическая гипотеза.

В состоянии ТД равновесия все микросостояния равновероятны. Это постулат равновероятности.

Пусть наша система состоит из одной частицы. Мы следим за скоростью частицы. Естественно нас интересует средняя скорость частицы:

.

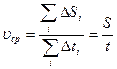Эргодическая гипотеза утверждает, что такая средняя скорость равняется средней скорости, вычисленной по ансамблю систем, т.е. среднее значение величины, вычисленное по времени равняется среднему значению величины, вычисленному по ансамблю систем.

Пусть число систем в ансамбле 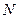, в некоторый момент времени :

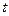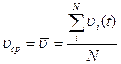
Впервые эта гипотеза была высказана в 1871 г. Л. Больцманом (1844-1906). Затем Дж. Максвелл в 1879 г. проанализировал возможность замены средних значений по времени средними значениями по ансамблю. Используя эту гипотезу, мы можем вопрос об изучении параметров системы, меняющихся со временем, свести к одномоментному усреднению по ансамблю!

Статистический вес Г: определяется числом микросостояний, реализующих данное макросостояние. Причем справедлив постулат равновероятности всех микросостояний.

Общее число микросостояний равно, очевидно, числу способов, которыми можно разместить 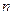частиц по 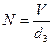ячейкам, где 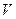- объем занимаемый системой из 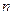частиц. Конкретную формулу дает комбинаторика. Отметим, что статистический вес для моля кислорода при нормальном атмосферном давлении и комнатной температуре 20°С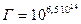

Статистический вес Г еще называют термодинамической вероятностью состояния системы. Т.к. это число способов, которыми может быть реализовано данное макросостояние системы, по определению, 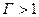. Таким образом, термодинамическая вероятность не есть вероятность в математическом смысле (т.к. ).

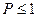Будем отличать макросостояния номерами 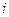, 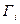- статистический вес 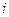-го макросостояния.

Используя это понятие, Больцман в 1872 г. Предложил статистическое толкование энтропии. Это более глубокое толкование.

Согласно Больцману, энтропия системы и статистический вес Г связаны между собой соотношением

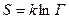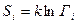или и

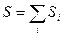- если система состоит из подсистем с .

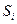Она определяется логарифмом числа микросостояний, с помощью которых было реализовано данное макросостояние.

Тогда статистический вес системы выражается через произведение 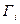подсистем.

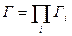
Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы.

Формула Больцмана позволяет дать энтропии следующее определение (статистическое толкование).

Энтропия является мерой неупорядоченности системы. Энтропия есть количественная мера беспорядка системы многих частиц.

В самом деле, чем больше число микросостояний реализующих данное макросостояние, тем больше энтропия.

В изолированной ТД системе все процессы идут в направлении возрастания энтропии, в направлении наиболее вероятного макросостояния (равновесного). Энтропия возрастает по II началу ТД, следовательно, естественные процессы стремятся перевести систему в состояние с наибольшим беспорядком. Это тенденция, хотя возможны отдельные флуктуации, понижающие энтропию.

Ø Ранее мы рассматривали, что в типичных условиях одна частица приходится на 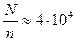«ячеек». В соответствии со сказанным можно заключить, что с течением времени число частиц в некотором, выделенном в системе, объеме не остается постоянным, а все время изменяется в небольших пределах. Большие отклонения в принципе так же возможны, но маловероятны и поэтому встречаются чрезвычайно редко. Среднее по времени число частиц в объеме вычислить нельзя, однако можно воспользоваться эргодической гипотезой и свести среднее по времени к среднему по ансамблю систем и вычислить эту величину. Получается, средняя плотность в выделенном объеме равна средней плотности в объеме всей системы.

Флуктуации. Говорят, что величина флуктуирует, если ее значение колеблется около среднего. В статистической физике и термодинамике обычно имеются в виду флуктуации внутренних параметров в состоянии термодинамического равновесия.

Мерой флуктуаций является стандартное отклонение от среднего значения, которое определено равенством для дискретных величин:

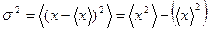
При вычислении этой величины усреднение по времени можно заменить усреднением по ансамблю.

Стандартное отклонение растет медленнее, чем общее число частиц в системе, в то время как среднее растет пропорционально числу частиц в системе. Следовательно, относительное стандартное отклонение убывает сростом числа частиц в системе.

Расчет относительной величины флуктуации с помощью распределения Пуассона дает величину:

.

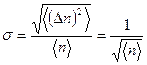Отметим, что относительная роль флуктуаций возрастает с уменьшением области, в которой эти флуктуации рассматриваются. Если область стремится к величине объема системы, то число частиц в этой области стремится к числу частиц системы.

Так как флуктуации уменьшаются как 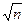, следовательно, с ростом числа частиц в макросистемах флуктуации становятся ничтожно малыми.

Поэтому поведение системы большого числа частиц можно описывать с помощью средних величин, характеризующих систему.