Анализ локальной оптимальности дифференциальной игры
Учитывая, что 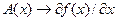 при
при 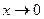 , значение матрицы
, значение матрицы 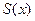 стремится к решению алгебраического уравнения (2.57) в начале координат
стремится к решению алгебраического уравнения (2.57) в начале координат
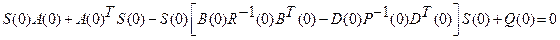 , (2.63)
, (2.63)
т.е. 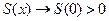 . При этом матрицы
. При этом матрицы 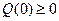 ,
, 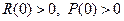 , а матрица
, а матрица
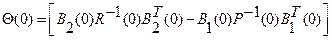 (2.70)
(2.70)
остается, по крайней мере, положительно полуопределенной.
Таким образом, в малой окрестности нуля система с управлением, реализованным с использованием SDRE-метода, сколь угодно близка линейной оптимальной системе
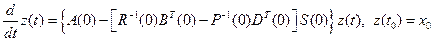 . (2.71)
. (2.71)
Это приближение является асимптотически оптимальным в том смысле, что управление сходится к оптимальному при 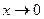 . Вслед за [36] найдем необходимые условия оптимальности регулятора нелинейным объектом в постановке дифференциальной игры. При этом будем полагать, что справедливы все предположения, сделанные в § 2.7.
. Вслед за [36] найдем необходимые условия оптимальности регулятора нелинейным объектом в постановке дифференциальной игры. При этом будем полагать, что справедливы все предположения, сделанные в § 2.7.
Предположение 2.8.1. Матрицы 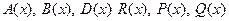 вместе с градиентами
вместе с градиентами 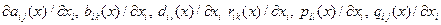 , где
, где
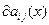 ,
, 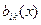 ,
, 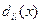 ,
, 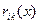 ,
, 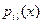 ,
, 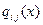 ,
, 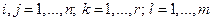 − элементы соответствующих матриц, непрерывны и ограничены
− элементы соответствующих матриц, непрерывны и ограничены 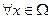 .
.
Теорема 2.8.1.В общем многомерном случае ( 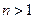 ) SDRE-управление нелинейным объектом
) SDRE-управление нелинейным объектом
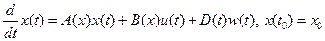 (2.72)
(2.72)
определяется необходимым условием оптимальности:
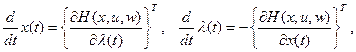 (2.73)
(2.73)
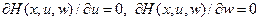 , (2.74)
, (2.74)
при этом, если выполняется предположение (2.8.1), второе уравнение (2.74) выполняется асимптотически с квадратичной нормой.
Доказательство.Запишем гамильтониан
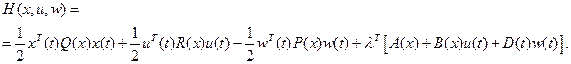 (2.75)
(2.75)
Используя (2.74) и второе уравнение (2.73), будем иметь
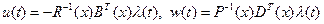 , (2.76)
, (2.76)
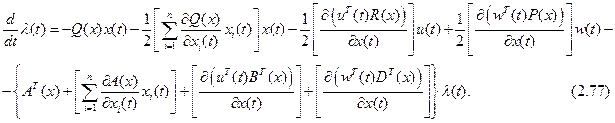
Вектор определялся ранее в виде 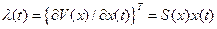 . В силу этого
. В силу этого
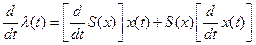 . (2.78)
. (2.78)
Учитывая (2.72), (2.76) и приравнивая (2.77) и (2.78), получим
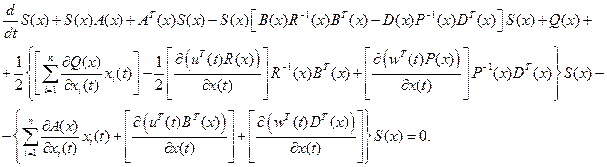
Если уравнение
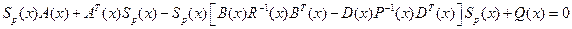 (2.79)
(2.79)
поточечно определяет положительно определенную матрицу 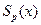 при
при 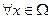 , то уравнение
, то уравнение
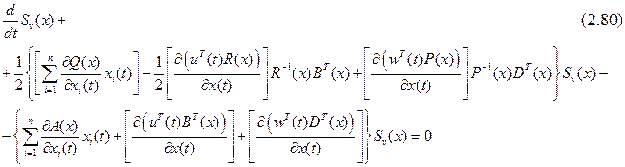
с начальным условием 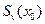 , определяемым решением уравнения
, определяемым решением уравнения
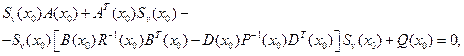
определяет динамику изменения матрицы 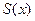 при
при 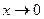 .
.
Дата добавления: 2019-10-16; просмотров: 564;
