Линейный гармонический осциллятор.
Линейным гармоническим осциллятором называется частица с массой m, которая движется вдоль некоторой оси под действием квазиупругой силы, пропорциональной отклонению частицы от положения равновесия 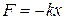 , k – коэффициент квазиупругой силы, связанный с массой частицы и собственной циклической частотой ее колебаний
, k – коэффициент квазиупругой силы, связанный с массой частицы и собственной циклической частотой ее колебаний 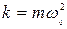 .
.
Потенциальная энергия гармонического осциллятора
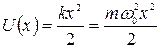 .
.
Модель гармонического осциллятора имеет большое значение в физике, как в классической (пружинный, физический, математический маятники), так и в квантовой. Например, при объяснении законов теплового излучения черного тела.
С классической точки зрения амплитуда колебаний гармонического осциллятора определяется запасом его полной энергии. В точках максимального отклонения 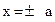 , где а – амплитуда колебаний классического осциллятора, кинетическая энергия равна нулю и вся энергия переходит в потенциальную. За пределы области (-а, +а) классический осциллятор выйти не может, т.е. частица в этом случае находится в потенциальной яме, имеющей форму параболы (рис.4).
, где а – амплитуда колебаний классического осциллятора, кинетическая энергия равна нулю и вся энергия переходит в потенциальную. За пределы области (-а, +а) классический осциллятор выйти не может, т.е. частица в этом случае находится в потенциальной яме, имеющей форму параболы (рис.4).
В квантовой механике задача о колебаниях линейного гармонического осциллятора решается с помощью уравнения Шредингера. Для линейного осциллятора оно имеет вид
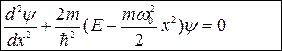
В теории дифференциальных уравнений доказывается, что это уравнение имеет конечные, однозначные и непрерывные решения при значениях параметра Е, удовлетворяющих соотношению
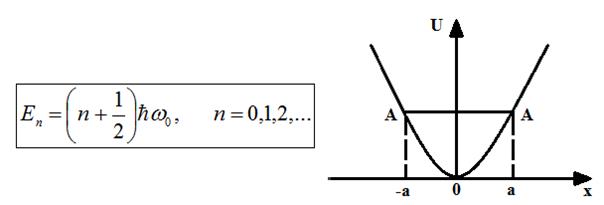
Рис.4
Получается, что энергия квантового осциллятора может иметь только дискретные значения, т.е. квантуется.На рисунке 5 представлена схема энергетических уровней гармонического квантового осциллятора. Уровни энергии являются эквидистантными, т.е. отстоят друг от друга на одинаковое расстояние. Вычисления для гармонического квантового осциллятора вероятности переходов квантовой системы из одного состояния в другое показали, что для него возможны лишь переходы между соседними уровнями. При таких переходах квантовое число n изменяется на единицу: 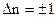 .
.
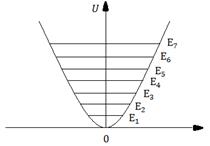
Рис.5
Условия, накладываемые на изменения квантовых чисел при переходах системы из одного состояния в другое, называются правилами отбора. В случае гармонического осциллятора правило отбора допускает изменение энергии осциллятора только порциями 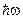 . Этот результат, полученный в квантовой механике, совпадает с предположением, которое пришлось ранее выдвинуть Планку, вопреки законам классической физики, чтобы вычислить испускательную способность абсолютно черного тела.
. Этот результат, полученный в квантовой механике, совпадает с предположением, которое пришлось ранее выдвинуть Планку, вопреки законам классической физики, чтобы вычислить испускательную способность абсолютно черного тела.
Еще один важный результат - наименьшее возможное значение энергии равно
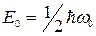
Это значение называется нулевой энергией.
Если учесть волновые свойства частицы внутри потенциальной ямы, каковым является квантовый гармонический осциллятор, то соотношение неопределенностей также приводит к результату: полная энергия осциллятора и амплитуда его колебаний не могут быть равны нулю.
Вэтом случае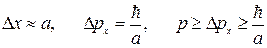 .
.
При этом энергия удовлетворяет соотношению
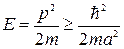 .
.
Полная энергия гармонического осциллятора равна его максимальной потенциальной энергии
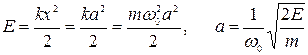
Получили выражение для амплитуды колебаний, которое подставим в выражение для энергии, полученное из соотношения неопределенности,
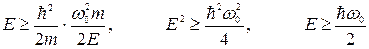
Существование нулевой энергии подтверждается экспериментами по изучению рассеяния света кристаллами при сверхнизких температурах. Рассеяние света происходит на тепловых колебаниях, которые совершают атомы, молекулы или ионы, расположенные в узлах кристаллической решетки. С классической точки зрения интенсивность рассеянного света должна убывать до нуля с понижением температуры до 0 К, так как должны прекратиться тепловые колебания узлов решетки, на которых происходит рассеяние. Опыты показали, что при уменьшении температуры интенсивность рассеянного света стремиться к некоторому предельному значению, неубывающему при дальнейшем охлаждении кристалла. То есть при Т→ 0 у частиц, расположенных в узлах решетки, сохраняются некоторые нулевые колебания, на которых и происходит рассеяние света. Нулевым колебаниям соответствует нулевая энергия атомных осцилляторов.
Строгое решение задачи о квантовом осцилляторе приводит еще к одному значительному отличию квантового осциллятора от классического. Оказывается, что можно обнаружить частицу за пределами дозволенной области 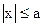 . Таким образом, имеется отличная от нуля вероятность обнаружить частицу в той области, которая является классически запрещенной. На рисунке 6 приводится график распределения плотности вероятности обнаружения частицы для состояния n = 1. За пределами дозволенного интервала полная энергия частицы будет меньше ее потенциальной энергии (следовательно, кинетическая энергия должна быть отрицательной). С подобной ситуацией мы сталкивались при рассмотрении туннельного эффекта.
. Таким образом, имеется отличная от нуля вероятность обнаружить частицу в той области, которая является классически запрещенной. На рисунке 6 приводится график распределения плотности вероятности обнаружения частицы для состояния n = 1. За пределами дозволенного интервала полная энергия частицы будет меньше ее потенциальной энергии (следовательно, кинетическая энергия должна быть отрицательной). С подобной ситуацией мы сталкивались при рассмотрении туннельного эффекта. 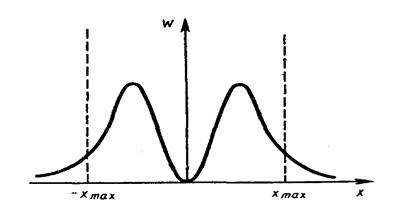
Рис.6
Вопросы для самоконтроля:
1. В чем отличие решения задачи о потенциальном барьере в классическом и квантовом приближениях?
2. В чем смысл коэффициентов отражения и прозрачности?
3. Что такое туннельный эффект? Где он используется?
4. Что такое линейный гармонический осциллятор?
5. Каков смысл нулевой энергии квантового осциллятора?
Лекция 7.
АТОМ ВОДОРОДА.
План
1. Уравнение Шредингера для электрона в атоме водорода.
2. Главное n, орбитальное l и магнитное m квантовые числа; их физический смысл.
3. Условное обозначение состояний электрона. Правило отбора. Его физический смысл.
4. Понятие электронного облака. Его физический смысл.
Дата добавления: 2019-07-26; просмотров: 1644;
