ЕВКЛИДОВЫ ПРОСТРАНСТВА
Введение основного понятия
В произвольных абстрактных линейных пространствах над числовыми полями отсутствует возможность проведения измерений, как-то: длины вектора, расстояния между векторами и т. д. Это все при том, что в пространствах направленных отрезков подобные измерения возможны. Отсюда напрашивается вывод о необходимости введения некоторого универсального инструмента, с помощью которого измерения можно было бы осуществлять. Вспомним, что метрические понятия в пространствах направленных отрезков оказалось возможным выразить через понятие скалярного произведения. Но ведь само скалярное произведение определяется с помощью длины вектора и угла между направленными отрезками, чего в абстрактных пространствах как раз и нет. Решение задачи лежит в аксиоматизации свойств скалярного произведения направленных отрезков и переносе полученных аксиом в абстрактное вещественное пространство.
Определение 8.1. Пусть 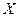 произвольное вещественное линейное пространство. Тогда скалярным произведением в Х назовем отображение
произвольное вещественное линейное пространство. Тогда скалярным произведением в Х назовем отображение 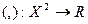 , удовлетворяющее следующим аксиомам:
, удовлетворяющее следующим аксиомам:
1. 
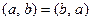 ;
;
2. 
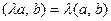 ;
;
3. 
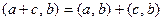 ;
;
4. 
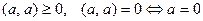 ;
; 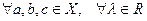 .
.
Пример 8.1. Очевидно, что обычное скалярное произведение направленных отрезков удовлетворяет этому определению.
Пример 8.2. Пусть 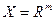 , тогда для векторов
, тогда для векторов  и
и 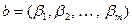 определим скалярное произведение формулой
определим скалярное произведение формулой 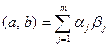 . Легко проверить, что все аксиомы выполняются.
. Легко проверить, что все аксиомы выполняются.
Пример 8.3. Пусть, как в примере 8.2, 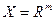 , и заданы положительные вещественные числа
, и заданы положительные вещественные числа 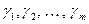 . Тогда скалярное произведение в этом же пространстве определим формулой
. Тогда скалярное произведение в этом же пространстве определим формулой 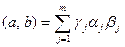 .
.
Пример 8.4. Пусть 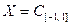 . Для произвольных функций
. Для произвольных функций 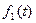 и
и 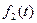 скалярное произведение можно определить формулой
скалярное произведение можно определить формулой  .
.
Из предложенных аксиом легко получить ряд следствий, именно:
1. 
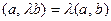 ;
;
2. 
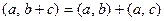 ;
;
3. 
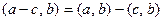 ;
;
4. 
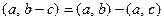 ;
; 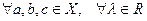 .
.
Наконец, для любых 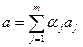 и
и 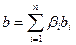 имеем:
имеем:
5. 
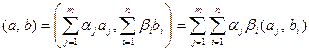 , для любых линейных комбинаций векторов пространства Х. Для доказательства последнего следствия можно использовать математическую индукцию.
, для любых линейных комбинаций векторов пространства Х. Для доказательства последнего следствия можно использовать математическую индукцию.
Определение 8.2. Евклидовым пространством 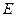 называется вещественное линейное пространство с введенным в нем скалярным произведением.
называется вещественное линейное пространство с введенным в нем скалярным произведением.
Из этого определения следует, что приведенные примеры 8.1 – 8.4 одновременно представляют и евклидовы пространства, первые три из которых конечномерные, а последнее бесконечномерно. Как и ранее, будем в дальнейшем работать только с конечномерными евклидовыми пространствами.
Ортогональность
Из определения скалярного произведения легко следует, что 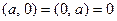 . В самом деле, например,
. В самом деле, например, 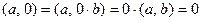 . Но здесь интересен общий случай.
. Но здесь интересен общий случай.
Определение 8.3. Пусть 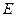 – евклидово пространство и
– евклидово пространство и 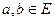 . Вектор
. Вектор  называется ортогональным к вектору
называется ортогональным к вектору  , если
, если 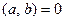 .
.
Ясно, что тогда и вектор  оказывается ортогональным вектору
оказывается ортогональным вектору  . Таким образом, это бинарное отношение симметрично. Отношение ортогональности часто обозначают
. Таким образом, это бинарное отношение симметрично. Отношение ортогональности часто обозначают  .
.
Лемма 8.1. Вектор, ортогональный к каждому вектору евклидова пространства, равен нулю.
Действительно, ведь тогда он ортогонален себе и по четвертой аксиоме обязан равняться нулю.
Следствие. Если 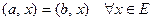 , то
, то 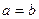 .
.
Определение 8.4. Система векторов называется ортогональной, если она состоит из одного ненулевого вектора или векторы ее составляющие попарно ортогональны.
Следующий результат связывает понятие ортогональности с понятием линейной независимости, что очевидно может иметь далеко идущие последствия.
Теорема 8.1. Ортогональная система, не содержащая нулевых векторов, линейно независима.
Доказательство. Случай одноэлементной системы тривиален. Пусть теперь задана ортогональная система 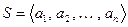 . По определению здесь
. По определению здесь 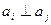 для
для 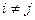 ,
, 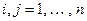 , и
, и 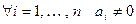 . Докажем линейную независимость системы
. Докажем линейную независимость системы  по критерию ЛНЗ. Составим линейную комбинацию векторов системы и приравняем ее нулю:
по критерию ЛНЗ. Составим линейную комбинацию векторов системы и приравняем ее нулю:
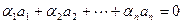 .
.
Умножим обе части равенства скалярно на вектор 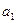 . Получим
. Получим
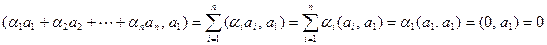 .
.
Тогда по четвертой аксиоме скалярного произведения получается, что 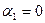 . Ясно, что в качестве множителя можно взять любой
. Ясно, что в качестве множителя можно взять любой 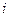 -й вектор системы и показать, что
-й вектор системы и показать, что  . Таким образом, по критерию ЛНЗ удостоверяемся в линейной независимости системы
. Таким образом, по критерию ЛНЗ удостоверяемся в линейной независимости системы  .
.
Определение 8.5. Вектор евклидова пространства называется нормированным, если его скалярный квадрат равен единице.
Любой ненулевой вектор можно нормировать, т.е. перейти к коллинеарному нормированному вектору. Действительно, пусть 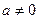 . Тогда для
. Тогда для 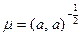 вектор
вектор 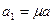 оказывается нормированным. Множитель
оказывается нормированным. Множитель 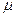 называется нормирующим множителем.
называется нормирующим множителем.
Определение 8.6. Система называется нормированной, если каждый вектор в ней нормирован.
Определение 8.7. Ортогональная и нормированная система называется ортонормированной.
Определение 8.8. Базисная ортонормированная система называется ортонормированным базисом. Сокращение – ОНБ. Если 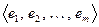 – ОНБ, то
– ОНБ, то
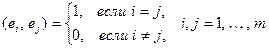 . (8.1)
. (8.1)
Хотя пока неизвестен факт существования ортонормированных базисов, можно сформулировать два простейших свойства этого объекта.
Теорема 8.2. Пусть 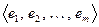 – ОНБ в
– ОНБ в 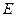 . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения:
1.  Если
Если 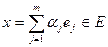 , то
, то 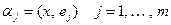 ;
;
2.  Система
Система 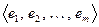 является ОНБ тогда и только тогда, когда
является ОНБ тогда и только тогда, когда 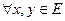 , где
, где 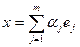 , а
, а 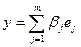 скалярное произведение этих векторов определяется формулой
скалярное произведение этих векторов определяется формулой 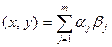 .
.
Доказательство 1  .Умножая скалярно обе части выражения
.Умножая скалярно обе части выражения 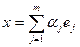 на вектор
на вектор 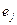 ,
, 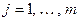 , и используя определение ОНБ, получаем требуемое.
, и используя определение ОНБ, получаем требуемое.
Доказательство 2  . Необходимость. Следствие 5
. Необходимость. Следствие 5  и определение сразу дают формулу скалярного умножения.
и определение сразу дают формулу скалярного умножения.
Достаточность. Пусть теперь скалярное произведение задано указанным в теореме способом. Тогда вектор 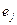 в данном базисе имеет координатную строку, в которой все компоненты, кроме
в данном базисе имеет координатную строку, в которой все компоненты, кроме 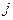 -ой равны нулю, а
-ой равны нулю, а 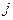 -я компонента равна единице. Поэтому оказывается справедливой формула (8.1). Что и требовалось.
-я компонента равна единице. Поэтому оказывается справедливой формула (8.1). Что и требовалось.
Рассмотрим теперь специальную процедуру получения ортогональных систем, из которой можно будет получить факт существования ОНБ.
Теорема 8.3 (метод ортогонализации Грама-Шмидта).
Пусть задана линейно независимая система 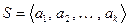 . Тогда существует эквивалентная ей ортогональная система
. Тогда существует эквивалентная ей ортогональная система 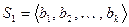 , которая может быть получена следующим образом:
, которая может быть получена следующим образом:
1. 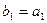 ;
;
2. 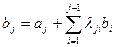 ,
, 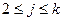 , где
, где 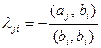 .
.
Доказательство. Докажем существование ортогональной системы эквивалентной  индукцией по числу векторов в
индукцией по числу векторов в  . Ясно, что содержательный смысл рассуждения по индукции в данном случае начинается с
. Ясно, что содержательный смысл рассуждения по индукции в данном случае начинается с 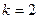 . Для
. Для 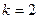 имеем:
имеем:
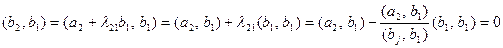 .
.
Здесь коэффициент 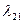 имеет смысл, ибо вектор
имеет смысл, ибо вектор  как вектор из линейно независимой системы. Очевидно, что системы
как вектор из линейно независимой системы. Очевидно, что системы 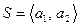 и
и 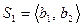 эквивалентны. Пусть теперь теорема справедлива для всех
эквивалентны. Пусть теперь теорема справедлива для всех 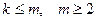 . Докажем результат для
. Докажем результат для 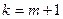 . Найдем скалярное произведение
. Найдем скалярное произведение 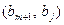 , где
, где 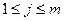 . Имеем:
. Имеем:
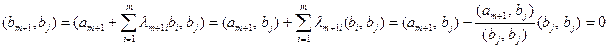 .
.
Как видим, в итоге получается ортогональная система. Каждый из коэффициентов 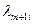 имеет смысл, ибо система
имеет смысл, ибо система  эквивалентна по индуктивному предположению линейно независимой системе
эквивалентна по индуктивному предположению линейно независимой системе  (
(  ) и потому не может содержать нулевых векторов (см. т. 5.5). Эквивалентность систем, состоящих из
) и потому не может содержать нулевых векторов (см. т. 5.5). Эквивалентность систем, состоящих из  векторов, легко следует из пункта 2 теоремы.
векторов, легко следует из пункта 2 теоремы.
Следствие 1. Ортонормированные базисы существуют.
Действительно, достаточно выбрать какой-либо базис в пространстве 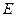 и подвергнуть его ортогонализации по схеме доказанной теоремы, а затем пронормировать получившиеся векторы.
и подвергнуть его ортогонализации по схеме доказанной теоремы, а затем пронормировать получившиеся векторы.
Следствие 2. Каждую ортонормированную систему можно дополнить до ортонормированного базиса.
Пример 8.5. Построить ортонормированный базис линейной оболочки  ,
,
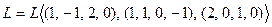 .
.
Скалярное произведение выберем такое же, как в примере 8.2 для 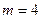 .
.
Легко проверяется линейная независимость системы, на которой построена линейная оболочка. Поэтому применим метод ортогонализации к данной системе. Имеем:
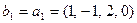 ;
;

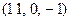 .
.
Для вычисления 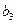 сначала вычислим коэффициенты
сначала вычислим коэффициенты 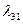 и
и 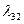 . Получим
. Получим
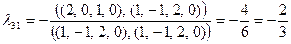 ;
; 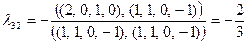 .
.
Поэтому
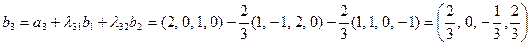 .
.
Проверка ортогональности системы 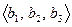 тривиальна. Подвергнем ее нормированию.
тривиальна. Подвергнем ее нормированию.
Нормирующие множители: 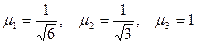 . Отсюда получаем ОНБ данной линейной оболочки:
. Отсюда получаем ОНБ данной линейной оболочки:
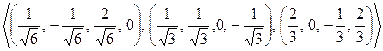
Задача. Выяснить, что произойдет, если процесс ортогонализации применить к линейно зависимой системе.
Определение 8.9. Пусть 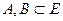 , где
, где 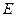 – евклидово пространство. Множество
– евклидово пространство. Множество 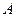 называется ортогональным к множеству
называется ортогональным к множеству 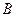 , если каждый вектор из
, если каждый вектор из 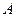 ортогонален каждому вектору из
ортогонален каждому вектору из 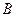 . Обозначение:
. Обозначение: 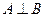 . Очевидно, что в этом случае и
. Очевидно, что в этом случае и 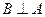 .
.
В основном в дальнейшем будем интересоваться случаем ортогональных подпространств.
Теорема 8.4. Для того чтобы подпространство  было ортогонально подпространству
было ортогонально подпространству 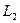 необходимо и достаточно, чтобы какой-либо базис
необходимо и достаточно, чтобы какой-либо базис  был ортогонален какому-либо базису
был ортогонален какому-либо базису 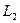 .
.
Доказательство. Необходимость очевидна.
Достаточность. Пусть базисом  будет
будет 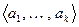 , а базисом
, а базисом 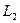 –
– 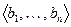 . Эти базисы ортогональны друг другу. Тогда любой вектор из
. Эти базисы ортогональны друг другу. Тогда любой вектор из  представится в виде
представится в виде  , а любой вектор из
, а любой вектор из 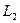 – в виде
– в виде 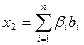 . Остается рассмотреть скалярное произведение:
. Остается рассмотреть скалярное произведение:
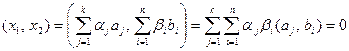 .
.
Определение 8.10. Сумма подпространств называется ортогональной, если слагаемые в ней попарно ортогональны. Обозначение: 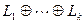 , для
, для  .
.
Лемма 8.2. Ортогональная сумма является прямой суммой.
Этот результат есть простое следствие второго критерия прямой суммы (см. т. 5.8).
Определение 8.11. Пусть 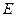 – евклидово пространство и
– евклидово пространство и 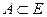 – произвольное непустое подмножество. Тогда ортогональным дополнением к А в Е называют множество векторов из Е ортогональных к А. Обозначение:
– произвольное непустое подмножество. Тогда ортогональным дополнением к А в Е называют множество векторов из Е ортогональных к А. Обозначение: 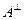 . Иными словами
. Иными словами 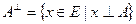 .
.
Лемма 8.3. Ортогональное дополнение к произвольному непустому подмножеству в Е есть подпространство в Е.
Доказательство представляет собой простое упражнение на применения критерия подпространства (см. т. 5.1).
Теорема 8.5 (о разложении евклидова пространства).
Для любого полпространства  евклидова пространства Е справедливо представление:
евклидова пространства Е справедливо представление: 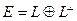 .
.
Доказательство. Пусть 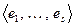 будет ОНБ в
будет ОНБ в  , а
, а  – ОН базис в
– ОН базис в  . Покажем, что объединенная система является базисом в Е. Объединенная система очевидно ортонормированная. Если она не является базисом в Е, то она может быть дополнена до ОНБ по следствию 2 из теоремы 8.3. Пусть одним из дополняющих векторов будет
. Покажем, что объединенная система является базисом в Е. Объединенная система очевидно ортонормированная. Если она не является базисом в Е, то она может быть дополнена до ОНБ по следствию 2 из теоремы 8.3. Пусть одним из дополняющих векторов будет  . Тогда этот вектор ортогонален базису
. Тогда этот вектор ортогонален базису  , и значит, ортогонален
, и значит, ортогонален  . Тогда
. Тогда 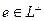 . С другой стороны, вектор
. С другой стороны, вектор  ортогонален базису
ортогонален базису  , значит, ортогонален
, значит, ортогонален  .
.
Отсюда по лемме 8.1 получаем, что 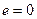 . Таким образом, дополнения до базиса объединенной системы не существует, т.е. она сама является ОН базисом Е. Что доказывает теорему.
. Таким образом, дополнения до базиса объединенной системы не существует, т.е. она сама является ОН базисом Е. Что доказывает теорему.
Добавим к сказанному несколько свойств ортогонального дополнения:
1. 
 ;
;
2. 
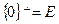 ;
;
3. 
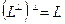 ;
;
4. 
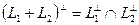 ;
;
5. 
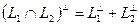 ;
; 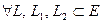 подпространств.
подпространств.
Доказательство 3  . Ясно, что
. Ясно, что 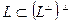 . С другой стороны, из предыдущей теоремы получаем:
. С другой стороны, из предыдущей теоремы получаем: 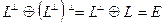 . Теперь из соображений размерности имеем требуемое.
. Теперь из соображений размерности имеем требуемое.
Доказательство 4  .
.  ,
, 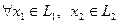 ;
; 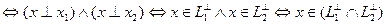 .
.
Измерения в евклидовом пространстве
В этом параграфе станет понятной причина введения скалярного произведения в произвольном вещественном пространстве. Но приходится начинать несколько издалека. Сначала докажем одно универсальное неравенство.
Теорема 8.6 (неравенство Коши-Буняковского).
Для любых двух векторов 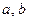 евклидова пространства
евклидова пространства  справедливо неравенство:
справедливо неравенство:
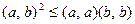 .
.
Доказательство. Заметим сразу, что если один из векторов равен нулю, то неравенство становится тривиальным. Будем считать, что векторы не равны нулю. Тогда легко получим:
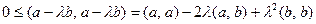 .
.
Выберем множитель 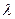 специальным образом. Пусть
специальным образом. Пусть 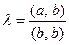 . Тогда имеем
. Тогда имеем
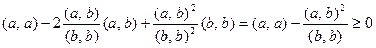 ,
,
что доказывает утверждение.
Пример 8.6. Для пространства 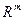 со стандартным скалярным произведением из примера 8.2 неравенство К-Б выглядит традиционным образом: пусть
со стандартным скалярным произведением из примера 8.2 неравенство К-Б выглядит традиционным образом: пусть 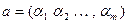 ,
, 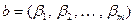 , то
, то
 ,
,
или
 .
.
Неравенство в теореме 8.6 нестрогое. Представляет интерес вопрос о достижении в нем равенства.
Лемма 8.4. Равенство в неравенстве Коши-Буняковского достигается тогда и только тогда, когда перемножаемые векторы коллинеарны.
Доказательство. Необходимость. Вновь считаем, что 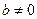 . Тогда его можно переписать в виде
. Тогда его можно переписать в виде
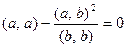
или 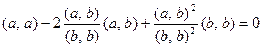 .
.
Выбирая 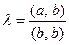 получим, что
получим, что 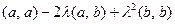
 .
.
Таким образом, скалярный квадрат равен нулю, следовательно 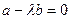 , т.е.
, т.е. 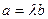 .
.
Достаточность. Если 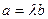 , то получаем с одной стороны
, то получаем с одной стороны 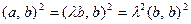 , а с другой –
, а с другой –  , что завершает доказательство.
, что завершает доказательство.
Определим теперь основные метрические понятия в евклидовом пространстве.
Определение 8.12. Пусть 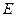 – евклидово пространство и
– евклидово пространство и 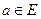 , тогда длиной вектора а называется вещественное число
, тогда длиной вектора а называется вещественное число 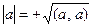 , т.е. арифметический корень квадратный из скалярного квадрата вектора.
, т.е. арифметический корень квадратный из скалярного квадрата вектора.
Это определение подчиняется естественным свойствам длины:
1. 
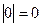 ;
;
2. 
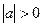 , если
, если 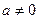 ;
;
3. 
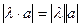 – свойство абсолютной однородности.
– свойство абсолютной однородности.
Определение 8.13. Пусть 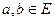 – ненулевые векторы. Тогда косинусом угла между данными векторами называется величина
– ненулевые векторы. Тогда косинусом угла между данными векторами называется величина
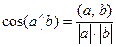 ,
, 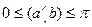 .
.
Если хотя бы один вектор нулевой, то угол считается неопределенным.
Это определение нуждается в пояснении, ибо в правой части равенства стоит обозначение вполне определенной функции косинус. Можно ли гарантировать указанной правой частью, что перед нами функция косинус? В пользу такого определения говорят следующие факты. Во-первых, из неравенства Коши-Буняковского следует, что правая часть равенства не превосходит по модулю единицы, что согласуется с определением косинуса; во-вторых, случай коллинеарности доставляет значение угла 0 или 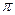 ; в третьих, ортогональность а и
; в третьих, ортогональность а и  дает значение угла, равное
дает значение угла, равное  ; наконец, в четвертых, видно, что умножение векторов на положительные числа не меняют величины угла. Все это говорит о том, что данное определение является вполне разумным.
; наконец, в четвертых, видно, что умножение векторов на положительные числа не меняют величины угла. Все это говорит о том, что данное определение является вполне разумным.
Рассмотрим некоторые известные факты из школьной геометрии применительно к геометрии евклидова пространства. Пусть вновь заданы два ненулевых вектора  . Будем рассматривать их как две стороны обобщенного треугольника. Тогда третьей стороной естественно объявить разность
. Будем рассматривать их как две стороны обобщенного треугольника. Тогда третьей стороной естественно объявить разность 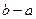 , вспоминая направленные отрезки. Вычислим квадрат длины третьей стороны, используя формулу для угла:
, вспоминая направленные отрезки. Вычислим квадрат длины третьей стороны, используя формулу для угла:
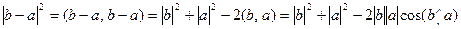 .
.
В итоге получаем известную теорему косинусов. В случае, если 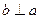 , то построенный треугольник является прямоугольным. И из последней формулы получаем теорему Пифагора:
, то построенный треугольник является прямоугольным. И из последней формулы получаем теорему Пифагора: 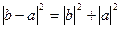 . Из той же формулы можно получить известные соотношения между длинами сторон треугольника, если оценивать множитель
. Из той же формулы можно получить известные соотношения между длинами сторон треугольника, если оценивать множитель 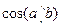 сверху и снизу, а именно:
сверху и снизу, а именно:
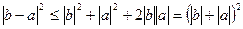 ,
,
и тогда 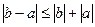 .
.
Или 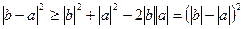 ,
,
и тогда 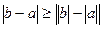 .
.
Введем, наконец, понятие расстояния между двумя векторами евклидова пространства.
Определение 8.14. Расстоянием между двумя векторами  и
и  евклидова пространства
евклидова пространства 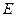 называется вещественное число
называется вещественное число 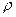 , определяемое соотношением
, определяемое соотношением
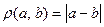 .
.
Так определенная двуместная функция действительно может рассматриваться как функция расстояния. Она обладает следующими свойствами:
1. 
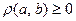 ;
;
2. 
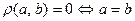 ;
;
3. 
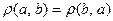 ;
;
4. 
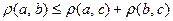 – неравенство треугольника;
– неравенство треугольника; 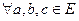 .
.
Последнее неравенство легко доказывается, если в первом соотношении для длин сторон треугольника сделать замену  ,
, 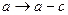 .
.
Определение 8.15. Непустое множество М называется метрическим пространством, если для него определено отображение 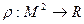 , обладающее указанными свойствами 1
, обладающее указанными свойствами 1  – 4
– 4  .
.
С точки зрения последнего определения в случае с евклидовым пространством имеем дело с пространством метрическим. Таким образом, отчасти поставленная в начале главы цель выполнена. Но есть еще и некоторые другие задачи. В завершение параграфа дадим еще одно определение.
Определение 8.16. Пусть 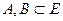 – два непустых подмножества евклидова пространства. Тогда расстоянием между множествами А и В называется величина
– два непустых подмножества евклидова пространства. Тогда расстоянием между множествами А и В называется величина

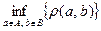 .
.
Вопрос. Чему равно расстояние между двумя подпространствами в Е?
Ортогональное проектирование на подпространство
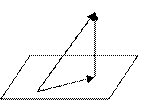 Задача ортогонального проектирования в наглядных пространствах решается весьма просто. Например, в трехмерном пространстве
Задача ортогонального проектирования в наглядных пространствах решается весьма просто. Например, в трехмерном пространстве  при проектировании на пространство
при проектировании на пространство  это можно представить в виде чертежа. Здесь видно, что вектор-наклонная может быть
это можно представить в виде чертежа. Здесь видно, что вектор-наклонная может быть
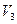 а h
а h
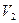 g
g
представлен, причем однозначно, в виде суммы ортогональной проекции 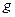 и вектора h – ортогональной составляющей. Таким образом, имеем равенство
и вектора h – ортогональной составляющей. Таким образом, имеем равенство 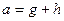 , где
, где  . Но в произвольном евклидовом пространстве теорема 8.5 доставляет такую же возможность. Пусть
. Но в произвольном евклидовом пространстве теорема 8.5 доставляет такую же возможность. Пусть  будет произвольным подпространством в Е. Тогда, как известно,
будет произвольным подпространством в Е. Тогда, как известно, 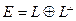 , что на уровне отдельных векторов означает: для любого вектора
, что на уровне отдельных векторов означает: для любого вектора 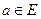 справедливо однозначное представление
справедливо однозначное представление 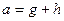 , где
, где  , т.е.
, т.е. 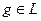 , а
, а 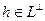 . Вектор
. Вектор 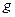 называется ортогональной проекцией вектора
называется ортогональной проекцией вектора  на подпространство
на подпространство  , а вектор
, а вектор 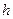 – перпендикуляром. Вектор
– перпендикуляром. Вектор  естественно назвать наклонной. Векторы
естественно назвать наклонной. Векторы 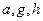 составляют прямоугольный треугольник в Е. Поэтому справедлива теорема Пифагора:
составляют прямоугольный треугольник в Е. Поэтому справедлива теорема Пифагора:

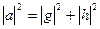 .
.
Отсюда понятно, что длина проекции не превосходит длины наклонной:  . То же можно сказать и о длине перпендикуляра, Это хорошо согласуется с нашими представлениями в наглядных пространствах.
. То же можно сказать и о длине перпендикуляра, Это хорошо согласуется с нашими представлениями в наглядных пространствах.
Пусть теперь 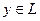 . Рассмотрим равенство
. Рассмотрим равенство
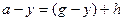 , где
, где 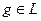 и
и 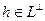 .
.
Тогда, ввиду того, что 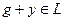 , получаем
, получаем
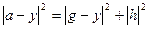 .
.
Значит, 
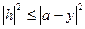 , откуда
, откуда 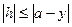 . При этом равенство достигается, очевидно, для
. При этом равенство достигается, очевидно, для 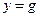 . Последнее означает, что ближайшим вектором к вектору
. Последнее означает, что ближайшим вектором к вектору  в
в  есть его ортогональная проекция на
есть его ортогональная проекция на  . Так что
. Так что  .
.
Определение 8.17. Углом между вектором и подпространством называется наименьший из углов, которые образует данный вектор с векторами подпространства.
Попробуем описать этот угол. Пусть 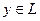 – произвольный ненулевой вектор из подпространства. Тогда
– произвольный ненулевой вектор из подпространства. Тогда
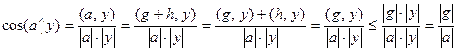 .
.
По следствию из леммы 8.4 функция косинус примет наибольшее значение, а при этом величина угла будет наименьшей, тогда и только тогда, когда вектор 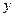 будет коллинеарен вектору
будет коллинеарен вектору 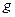 . Таким образом, наименьшим из углов вектора с векторами из подпространства является угол между данным вектором и его ортогональной проекцией на это подпространство.
. Таким образом, наименьшим из углов вектора с векторами из подпространства является угол между данным вектором и его ортогональной проекцией на это подпространство.
Введем обозначения: если 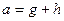 , где
, где  , т.е.
, т.е. 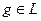 , а
, а 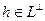 , то обозначим
, то обозначим 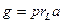 , а
, а 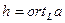 . Следовательно, имеем дело с векторными функциями
. Следовательно, имеем дело с векторными функциями 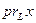 и
и 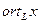 для произвольного
для произвольного 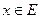 . Рассмотрим алгебраические свойства проекции и перпендикуляра. Сначала перечислим некоторые из свойств.
. Рассмотрим алгебраические свойства проекции и перпендикуляра. Сначала перечислим некоторые из свойств.
1. 
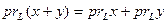 ;
;
2. 
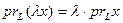 ;
;
3 
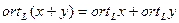 ;
;
4. 
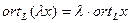 ;
;
5. 
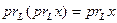 ;
;
6. 
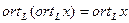 ;
;
7. 
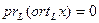 ;
;
8. 
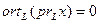 ;
;
9. 
 ;
;
10. 
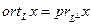 ;
;
11. 
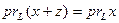 ;
;
12. 
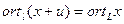 ;
;
для любых 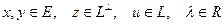 .
.
Все эти свойства доказываются весьма просто, исходя из определения. Например, докажем 1  – 4
– 4  , т.е. линейные свойства проекции. Имеем
, т.е. линейные свойства проекции. Имеем
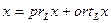 ,
,
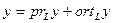 .
.
Складывая почленно, получаем
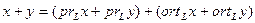 .
.
Умножая первое соотношение на 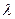 , получаем
, получаем
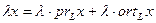 .
.
Учитывая, что первая группа слагаемых принадлежит  , а вторая –
, а вторая –  , заключаем, что
, заключаем, что
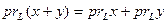 , а
, а 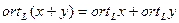 ,
,
аналогично
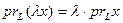 и
и 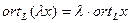 .
.
Здесь дополнительно воспользовались тем фактом, что сумма 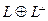 – прямая (лемма 8.2).
– прямая (лемма 8.2).
Рассмотрим дополнительно возможность ортогонального проектирования на ортогональную сумму. Пусть 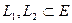 и
и 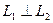 – подпространства. Тогда для произвольного вектора
– подпространства. Тогда для произвольного вектора 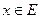 можно записать
можно записать
 .
.
Вектор в первых скобках, очевидно, принадлежит сумме 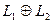 , а во вторых –
, а во вторых –  . Действительно,
. Действительно, 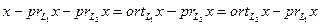 . Здесь первое представление ортогонально
. Здесь первое представление ортогонально  , а второе, ему равное, –
, а второе, ему равное, – 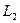 . Отсюда получаем, что
. Отсюда получаем, что
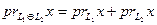 ,
,
Ортогональная составляющая равна одному из выражений
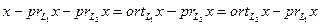 .
.
Евклидов изоморфизм
Как и в случае абстрактных линейных пространств, введем понятие изоморфизма, что позволит переносить многие результаты из пространств направленных отрезков, т.е. обычной геометрии, в евклидовы пространства.
Определение 8.18. Два евклидовых пространства 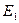 и
и 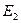 называются евклидово изомофными, если они изоморфны как вещественные пространства, т.е. существует изоморфизм
называются евклидово изомофными, если они изоморфны как вещественные пространства, т.е. существует изоморфизм 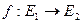 , и при этом для любых
, и при этом для любых 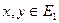 выполнено
выполнено
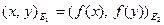 .
.
Разумеется, есть нужда в критерии евклидовой изоморфности.
Теорема 8.7 (критерий евклидовой изоморфности).
Два евклидовых пространства евклидово изоморфны тогда и только тогда, когда имеют одинаковую размерность.
Доказательство. Необходимость очевидна, ибо тогда данные пространства изоморфны как вещественные пространства (см. т. 5.9).
Достаточность. Пусть 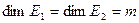 . Выберем ортонормированные базисы в указанных пространствах:
. Выберем ортонормированные базисы в указанных пространствах: 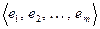 в
в 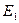 и
и 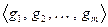 в
в 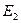 . Тогда для произвольных векторов
. Тогда для произвольных векторов 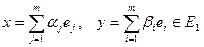 имеем с отображением
имеем с отображением 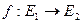
по правилу 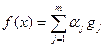 в силу свойства ортонормированных базисов:
в силу свойства ортонормированных базисов:
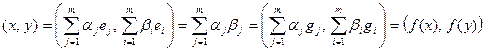 .
.
Само же отображение 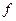 , очевидно, биективное и линейное. Например,
, очевидно, биективное и линейное. Например,
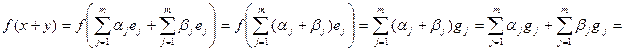
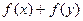 .
.
На основании понятия изоморфизма можно утверждать что результаты, справедливые в
трехмерном наглядном пространстве будут справедливыми в любом трехмерном подпространстве евклидова пространства, а значит в любом евклидовом пространстве.
Определитель Грама
В этом параграфе введем новый объект, обладающий многими интересными свойствами, некоторые из которых будут рассмотрены.
Определение 8.19. Пусть 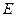 – евклидово пространство и
– евклидово пространство и 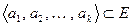 . Определителем Грама системы
. Определителем Грама системы 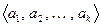 называется определитель вида
называется определитель вида
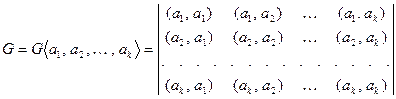 .
.
Во-первых докажем теорему, которую можно рассматривать как одно из свойств определителя Грама.
Теорема 8.8 (критерий линейной зависимости системы векторов).
Система векторов евклидова пространства линейно зависима тогда и только тогда, когда ее определитель Грама равен нулю.
Доказательство. Необходимость. Пусть система 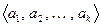 – линейно зависима. По первому критерию линейной зависимости (см. т. 5.3) существует ненулевой набор вещественных чисел
– линейно зависима. По первому критерию линейной зависимости (см. т. 5.3) существует ненулевой набор вещественных чисел 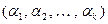 такой, что
такой, что
 .
.
Будем считать, для определенности, что 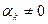 . Тогда умножая мысленно первые
. Тогда умножая мысленно первые 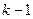 строку определителя соответственно на числа
строку определителя соответственно на числа 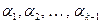 (их первые сомножители) и прибавляя к последней строке, умноженной на
(их первые сомножители) и прибавляя к последней строке, умноженной на 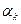 , получим, по известному свойству определителей, величину
, получим, по известному свойству определителей, величину 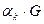 . Но этот определитель будет содержать в последней строке элементы
. Но этот определитель будет содержать в последней строке элементы 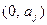 для
для 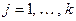 , т.е. будет содержать нулевую строку. Значит,
, т.е. будет содержать нулевую строку. Значит, 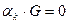 и тем самым
и тем самым 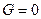 .
.
Достаточность. Пусть теперь 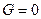 . Следовательно, его строки линейно зависимы. Это значит, что существует ненулевой набор
. Следовательно, его строки линейно зависимы. Это значит, что существует ненулевой набор 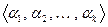 такой, что линейная комбинация строк с этими числами будет равна нулевой строке. В частности, в
такой, что линейная комбинация строк с этими числами будет равна нулевой строке. В частности, в 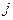 -ой позиции этой линейной комбинации будет присутствовать число
-ой позиции этой линейной комбинации будет присутствовать число 
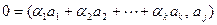 .
.
Если теперь каждый такой элемент умножить на 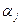 ,
, 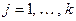 , и просуммировать по
, и просуммировать по 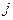 ,
,
от 1 до 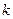 , то получим скалярный квадрат:
, то получим скалярный квадрат:
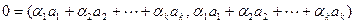 .
.
Если скалярный квадрат равен нулю, то сам вектор равен нулю. Значит,
 ,
,
т.е. система 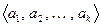 линейно зависима. Что и требовалось. Теорема доказана.
линейно зависима. Что и требовалось. Теорема доказана.
Рассмотрим некоторые другие свойства определителя Грама.
1.  Пусть система
Пусть система 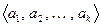 – линейно независима. Тогда
– линейно независима. Тогда
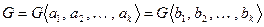 ,
,
где система 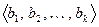 получена из системы
получена из системы 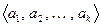 процессом ортогонализации Грама-Шмидта.
процессом ортогонализации Грама-Шмидта.
2.  Если система
Если система 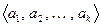 линейно независима, то
линейно независима, то  .
.
3. 
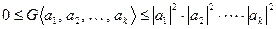 .
.
Равенство справа достигается тогда и только тогда, когда векторы попарно ортогональны или один из них равен нулю.
Доказательство первого свойства основано на применении формул ортогонализации и применяемых последовательно к первым сомножителям скалярных произведений, а потом ко вторым. Второе свойство является прямым следствием первого и теоремы 8.8. Докажем третье свойство, точнее правое неравенство. Из первого свойства имеем, что
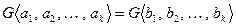 .
.
В силу того, что система 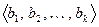 ортогональна, получаем, что
ортогональна, получаем, что
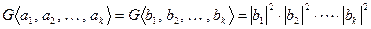 .
.
Остается показать, что для любого 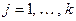
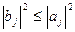 . Действительно,
. Действительно,
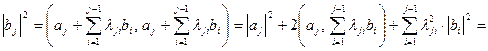
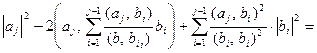
 =
=
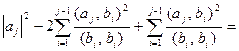
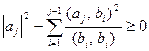 .
.
Так как в последнем неравенстве вычитается число неотрицательное, то имеем, что
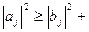
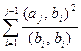 ,
,
т.е. 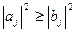 , что и требовалось.
, что и требовалось.
Задача о пересечении гиперплоскостей
Пусть 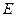 – евклидово пространство и
– евклидово пространство и 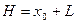 – гиперплоскость в нем. Как известно, если
– гиперплоскость в нем. Как известно, если 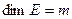 , то размерность направляющего подпространства
, то размерность направляющего подпространства 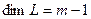 .
.
Естественно считать 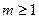 . Пусть
. Пусть 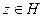 , тогда
, тогда 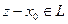 . Так как
. Так как 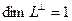 по теореме 8.5, то базис
по теореме 8.5, то базис  состоит из одного вектора, т.е.
состоит из одного вектора, т.е. 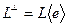 . Но тогда можно утверждать, что
. Но тогда можно утверждать, что 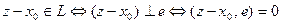 . Последнее равенство можно рассматривать как уравнение гиперплоскости. Учитывая, что
. Последнее равенство можно рассматривать как уравнение гиперплоскости. Учитывая, что 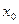 и
и  считаются известными, т.е.
считаются известными, т.е.  известное число, то уравнение гиперплоскости переписывается в виде
известное число, то уравнение гиперплоскости переписывается в виде
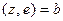 .
.
Пусть теперь заданы несколько гиперплоскостей, имеющих непустое пересечение:
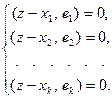 (8.2)
(8.2)
Как известно, непустое пересечение плоскостей есть плоскость (см. т. 5.10). В качестве
направляющего подпространства у этой плоскости служит пересечение направляющих подпространств пересекающихся плоскостей. Векторы сдвига в означенной системе можно заменить на один общий по известному свойству, например, 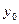 . Тогда система (8.2) преобразуется к виду
. Тогда система (8.2) преобразуется к виду
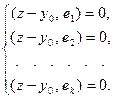 (8.3)
(8.3)
Сделаем замену: 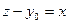 . Тогда система (8.3) запишется в виде:
. Тогда система (8.3) запишется в виде:
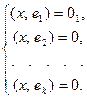 (8.4)
(8.4)
Если 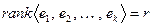 , то размерность пространства решений, или направляющего подпространства плоскости пересечения, очевидно, будет равна
, то размерность пространства решений, или направляющего подпространства плоскости пересечения, очевидно, будет равна 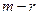 , ибо это размерность ортогонального дополнения к линейной оболочке
, ибо это размерность ортогонального дополнения к линейной оболочке 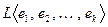 . Сдвигая это подпространство на вектор
. Сдвигая это подпространство на вектор 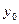 , получаем плоскость-решение системы.
, получаем плоскость-решение системы.
Так как при поиске векторов 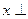
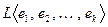 не является важным, через какую систему данное подпространство описано, то договоримся для большей простоты, что
не является важным, через какую систему данное подпространство описано, то договоримся для большей простоты, что 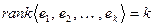 , а систему
, а систему 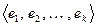 и неизвестный вектор
и неизвестный вектор 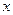 опишем в некотором ОНБ. Пусть
опишем в некотором ОНБ. Пусть 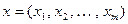 , а
, а 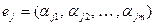 для
для 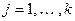 . Тогда
. Тогда
система (8.4) будет представлена в виде однородной системы линейных алгебраических уравнений:
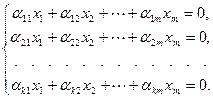
Общее решение такой системы, как известно, имеет размерность 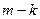 .
.
Если в системе (8.3) вычислить скалярные произведения 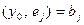 ,
, 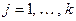 , то получим
, то получим
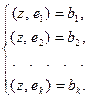
Тогда в координатной форме получим, вообще говоря, неоднородную СЛАУ вида
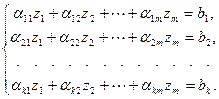
Здесь
