Using namespace std;

double Summa (int N, …)

{

va_list L; //Объявляем переменную для списка параметров

va_start (L, N); //Инициализируем переменную списка параметров

double R = 0;

for (int I = 0; I < N; ++ I)

R += va_arg (L, double); //Добавляем к R очередной аргумент

va_end (L); //Очищаем стек

Return R;

}

Int main ()

{

cout << Summa (3, 10.0, 20.0, 30.0) << endl; // 60

cout << Summa (5, 10.0, 20.0, 30.0, 40.0, 50.0) << endl; // 150

Return 0;

}

Рекурсивное использование функций

Функции внутри своего тела могут вызывать сами себя. Такой вызов называется рекурсией. На основе рекурсии можно строить очень интересные алгоритмы обработки данных.

Рассмотрим функцию возведения вещественного значения D в целую положительную степень P. Очевидная реализация этой функции основана на использовании цикла:

Double Pow (double D, unsigned P)

{

double R = 1;

for (unsigned I = 0; I < P; ++ I)

R *= D;

Return R;

}

А вот та же самая функция, реализованная на основе рекурсии:

Double Pow (double D, unsigned P)

{

If (P)

return Pow ( D, P – 1 ) * D;

Else

Return 1;

}

Основанием для рекурсии в этом примере послужило следующее рекуррентное соотношение:

Более сложный пример рекурсии основан на следующем рекуррентном соотношении (обычная реализация этого примера приведена в разделе 5.1 конспекта):

Через рекурсию это рекуррентное соотношение реализуется так:

Double T (unsigned n, double x)

{

Switch (n)

{

case 0:

Return 1;

case 1:

Return x;

default:

return 2 * x * T (n - 1, x) - T (n - 2, x);

}

}

Как видно из этих примеров алгоритм, реализуемый через рекурсию, выглядит более компактным и понятным по сравнению с обычной реализацией. С точки зрения эффективности, реализацию этих примеров через рекурсию вряд ли можно считать более эффективной, чем обычную реализацию. Это объясняется дополнительными затратами времени на многократный вызов функций и дополнительными затратами памяти (стека) на передачу аргументов.

Однако в ряде случаев использование рекурсии позволяет достичь существенного положительного эффекта.

Рассмотрим следующий пример: необходимо написать функцию для вычисления биномиальных коэффициентов:

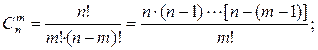n >= 0, 0 <= m <= n.

Значение биномиального коэффициента определяет число различных вариантов выбора m объектов из n объектов (как говорят, число сочетаний из n по m).

Основные свойства биномиальных коэффициентов:

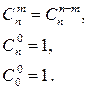
Максимальное значение биномиального коэффициента достигается при m = n / 2.

Очевидная реализация функции основана на использовании циклов для вычисления числителя и знаменателя биномиального коэффициента и нахождения частного от их деления: