Анализ резисторного усилителя на высоких частотах.

В области высоких частот емкостное сопротивление 1/jωC1 конденсатора С1 становится еще меньше, чем в области средних частот, поэтому его можно по-прежнему заменить коротким замыка­нием. Однако в области высоких частот надо учитывать влияние ем­костей 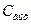, ,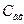С_м , так как их проводимости возрастают. Вследствие чего умень­шается емкостное сопротивление 1/jωC_о, увеличивается шунти­рующее действие.

С учетом вышесказанного эквивалентная схема резистивного усилителя в области верхних частот примет вид, изображенный на рис.6.2

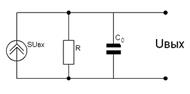
Рис.6.2. Эквивалентная схема резисторного каскада в области ВЧ.

По эквивалентной схеме (рис.6.2) определим выходное нап­ряжение и комплексный коэффициент усиления

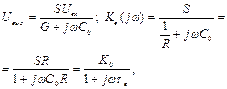(6.4)

где τ_в=С₀R- постоянная времени в области ВЧ.

Модуль коэффициента усиления на верхних частотах определяется выражением:

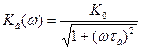(6.5)

и представляет собой частотную характеристику усилителя в области верхних частот (рис.6.3).

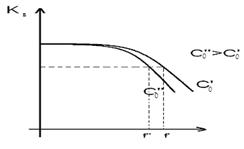
Рис.6.3. АЧХ в области ВЧ при различных значениях С₀.

С увеличением частоты 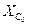уменьшается, вследствие чего увеличивается шунтирующее действие. По этой причине уменьшается выходное напряжение и коэффициент усиления.

Найдем верхнюю граничную частоту усилителя, на которой мо­дуль коэффициента усиления 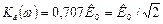. Следова­тельно, приравнивая (6.5.) к значению 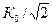, получим:

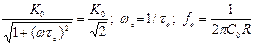. (6.6)

Из выражения (6.6) следует, что 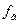обратно пропорционально емкости C₀. С уменьшением С₀ увеличивается верхная граничная частота и полоса пропускания усилителя (см. рис.6.3). Для расширения полосы пропускания в область высших частот необходимо уменьшать постоянную времени 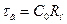. Емкость C₀ складывается из емкостей 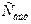, ,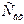С_м и зависит от выбранного усилительного элемента. Следовательно, уменьшение постоянной времени возможно лишь за счет уменьшения 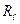. Однако это вызывает снижение коэффициента усиления 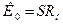(рис.6.4).

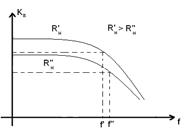
Рис.6.4. АЧХ в области ВЧ при различных значениях R_н.

Рассмотрим фазовый сдвиг, создаваемый усилителем в области верхних частот. Чтобы определить его, представим 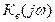в виде суммы вещественной и мнимой частей, для этого выражение 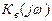умножим и разделим на комплексную величину, сопряженную со знаме­нателем:

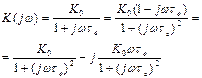(6.7)

Тангенс угла фазового сдвига равен отношению мнимой части к
вещественной:

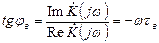(6.8)

С увеличением частоты 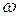фазовый сдвиг 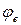асимптотически стремится к 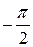. При 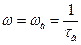, имеем

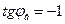; , (6.9)

т. е. верхней пороговой частоте соответствует фазовый сдвиг, рав­ный - 45° (см. рис.6.5.).

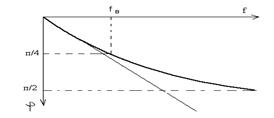
Рис.6.5. ФЧХ в области ВЧ.

Очевидно, при этой частоте модуль емкос­тной проводимости равен активной проводимости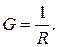

Выражая 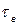через верхнюю пороговую частоту, можно записать уравнение фазочастотной характеристики для области высоких час­тот в виде

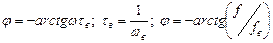. (6.10)

Коэффициент частотных искажений на верхней граничной часто­те определяется

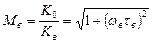(6.11)

Если заданы 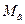и 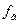, то из выражения (6.11) можно опреде­лить необходимое значение 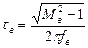и рассчитать требуемое сопротивление нагрузки:

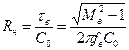. (6.12)

Таким образом, сопротивление нагрузки рассчитывается из необходимости удовлетворения основных технических условий усилите­ля в области верхних частот.