ГЕОМЕТРИЯ МАСС ТЕЛА ЧЕЛОВЕКА
Геометрией масс называется распределение масс между звеньями тела и внутри звеньев. Геометрия масс количественно описывается масс-инерционными характеристиками. Важнейшие из них — масса, радиус инерции, момент инерции и координаты центра масс.
Масса (т) —это количество вещества (в килограммах), содержащееся в теле или отдельном звене.
Вместе с тем масса — это количественная мера инертности тела по отношению к действующей на него силе. Чем больше масса, тем инертнее тело и тем труднее вывести его из состояния покоя или изменить его движение.
Массой определяются гравитационные свойства тела. Вес тела (в Ньютонах)
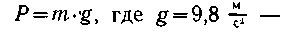 ускорение свободнопадающего тела.
ускорение свободнопадающего тела.
Масса характеризует инертность тела при поступательном движении. При вращении инертность зависит не только от массы, но и от того, как она распределена относительно оси вращения. Чем больше расстояние от звена до оси вращения, тем больше вклад этого звена в инертность тела. Количественной мерой инертности тела при вращательном движении служит момент инерции:
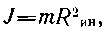
где Rин — радиус инерции — среднее расстояние от оси вращения (например, от оси сустава) до материальных точек тела.
Центром масс называется точка, где пересекаются линии действия всех сил, приводящих тело к поступательному движению и не вызывающих вращения тела. В поле гравитации (когда действует сила тяжести) центр масс совпадает с центром тяжести. Центр тяжести — точка, к которой приложена равнодействующая сил тяжести всех частей тела. Положение общего центра масс тела определяется тем, где находятся центры масс отдельных звеньев. А это зависит от позы, т. е. от того, как части тела расположены друг относительно друга в пространстве.
В человеческом теле около 70 звеньев. Но столь подробного описания геометрии масс чаще всего и не требуется. Для решения большинства практических задач достаточно 15-звенной модели человеческого тела (рис. 7). Понятно, что в 15-звенной модели некоторые звенья состоят из нескольких элементарных звеньев. Поэтому такие укрупненные звенья правильнее называть сегментами.
Цифры на рис. 7 верны для “среднего человека”, они получены путем усреднения результатов исследования многих людей. Индивидуальные особенности человека, и в первую очередь масса и длина тела, влияют на геометрию масс.
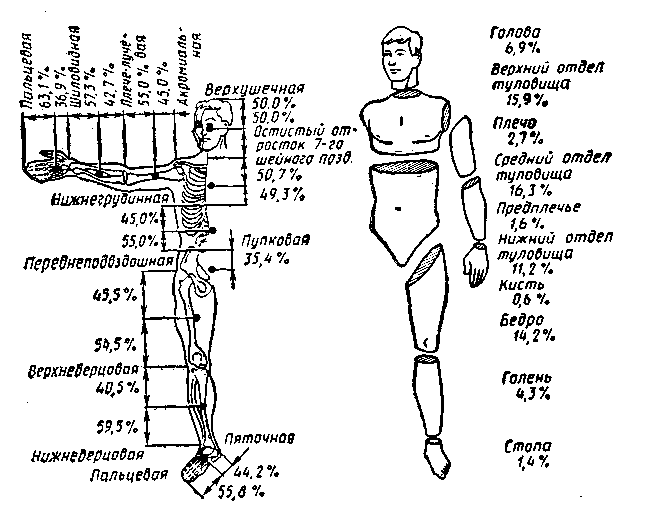
Рис. 7. 15 — звенная модель человеческого тела: справа — способ деления тела на сегменты и масса каждого сегмента (в % к массе тела); слева — места расположения центров масс сегментов (в % к длине сегмента)— см. табл. 1 (по В. М. Зациорскому, А. С. Аруину, В. Н. Селуянову)
В. Н. Селуянов установил, что массы сегментов тела можно определить с помощью следующего уравнения:
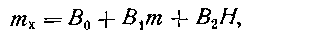
где mх — масса одного из сегментов тела (кг), например стопы, голени, бедра и т. д.; m —масса всего тела (кг); H —длина тела (см); В0, В1, В2 — коэффициенты регрессионного уравнения, они различны для разных сегментов (табл. 1).
Примечание. Величины коэффициентов округлены и верны для взрослого мужчины.
Для того чтобы уяснить, как пользоваться таблицей 1 и другими подобными таблицами, вычислим, например, массу кисти человека, у которого масса тела равна 60 кг, а длина тела 170 см.
Таблица 1
Коэффициенты уравнения для вычисления массы сегментов тела по массе (т) и длине (Я) тела
| Сегменты | Коэффициенты уравнения | ||
| В0 | В1 | В2 | |
| Стопа Голень Бедро Кисть Предплечье Плечо Голова Верхняя часть туловища Средняя часть туловища Нижняя часть туловища | —0,83 —1,59 —2,65 —0,12 0,32 0,25 1,30 8,21 7,18 —7,50 | 0,008 0,036 0,146 0,004 0,014 0,030 0,017 0,186 0,223 0,098 | 0,007 0,012 0,014 0,002 —0,001 —0,003 0,014 —0,058 —0,066 0,049 |
Масса кисти = - 0,12 + 0,004х60+0,002х170 = 0,46 кг. Зная, каковы массы и моменты инерции звеньев тела и где расположены их центры масс, можно решить много важных практических задач. В том числе:
— определить количество движения, равное произведению массы тела на его линейную скорость (m·v);
— определить кинетический момент, равный произведению момента инерции тела на угловую скорость (Jw); при этом нужно учитывать, что величины момента инерции относительно разных осей неодинаковы;
— оценить, легко или трудно управлять скоростью тела или отдельного звена;
— определить степень устойчивости тела и т. д.
Из этой формулы видно, что при вращательном движении относительно той же оси инертность человеческого тела зависит не только от массы, но и от позы. Приведем пример.
На рис. 8 изображена фигуристка, выполняющая вращение. На рис. 8, А спортсменка вращается быстро и делает около 10 оборотов в секунду. В позе, изображенной на рис. 8, Б, вращение резко замедляется и затем прекращается. Это происходит потому, что, отводя руки в стороны, фигуристка делает свое тело инертнее: хотя масса (m) остается той же, увеличивается радиус инерции (Rин) и, следовательно, момент инерции.
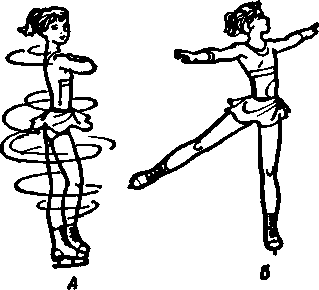
Рис. 8. Замедление вращения при изменении позы: А — меньшая; Б — большая величина радиуса инерции и момента инерции, который пропорционален квадрату радиуса инерции (I=m · Rин)
Еще одной иллюстрацией сказанному может быть шуточная задача: что тяжелее (точнее, инертнее)—килограмм железа или килограмм ваты? При поступательном движении их инертность одинакова. При круговом движении труднее перемещать вату. Ее материальные точки дальше отстоят от оси вращения, и поэтому момент инерции значительно больше.
Дата добавления: 2018-06-28; просмотров: 3830;
