Неуправляемый вентиль и его характеристики

Вентиль – прибор, проводящий ток в прямом направлении от анода к катоду. На рис. 3.4 показано условное обозначение вентиля, ВАХ идеального и реального диодов.

Для реальных диодов (кремниевых, германиевых и диодов Шоттки ) при одинаковых обратных напряжениях, обратные токи существенно различаются.

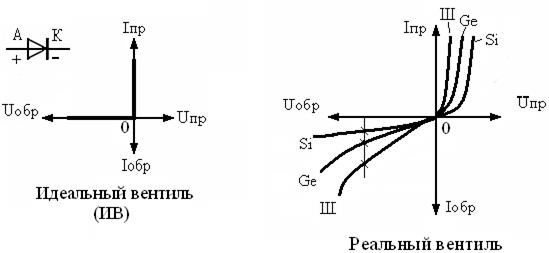
Рисунок 3.4 – Вольтамперные характеристики идеального и реального

вентилей

Здесь, процесс преобразования переменного тока в постоянный по направлению, происходит с потерями энергии. Для расчётов, реальную ВАХ заменяют линейно-ломанной, пренебрегая потерями от обратных токов, как это показано на рис.3.5а.

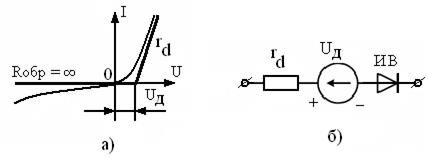
Рисунок 3.5 – Аппроксимация ВАХ реального вентиля (а) и его схема

замещения (б).

На рисунке 3.5 обозначено: U_д – начальное смещение ВАХ диода, r_d– дифференциальное сопротивление прямого участка ВАХ, ИВ – идеальный вентиль. Обычно начальное смещение ВАХ реальных диодов составляет 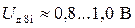; ; 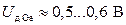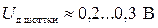. При такой аппроксимации, точность расчётов выпрямительных устройств, вполне удовлетворительна в широком диапазоне токов и напряжений.

К электрическим вентилям, работающим в схемах выпрямления предъявляется ряд требований:

1. Вентиль должен обеспечивать среднее значение прямого тока I_{пр ср} и

максимальное значение прямого тока I_{пр max}

2. Иметь минимально возможные r_d и U_д из-за потерь мощности в

прямом направлении, что поясняется рис. 3.6 и выражением (3.1) для

расчёта этих потерь.

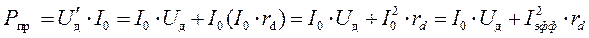(3.1)

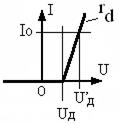
Рисунок 3.6 – К расчёту потерь вентиля в прямом направлении

3. Вентиль должен иметь малый обратный ток, поскольку это

дополнительные потери.

4. Обладать достаточной электрической прочностью в обратном

направлении U_{обр доп}.

5. При работе на ёмкость выдерживать ударный ток I_{пр уд}.

6. Иметь достаточное быстродействие – малое время восстановления обратного сопротивления.

Рассмотрим подробнее некоторые из этих требований.

Минимально возможные U_д, r_d – определяют КПД выпрямителя, что особенно важно в низковольтных схемах. Изготовители диодов, пытаясь уменьшить их массу и объём перегружают кристаллы полуповодников по току, плотность которого достигает 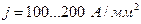. Это в 10…20 раз превышает оптимальные значения! Поэтому коэффициент загрузки диода по среднему току должен быть не более 0,2…0,3. Снизить потери в прямом направлении и увеличить КПД можно путём параллельного включения нескольких диодов. Если диоды дискретные (корпусные), то токи необходимо выравнивать путем включения дополнительных резисторов с сопротивлением R_доб > r_{d ,} как показано на рис.3.7 _.

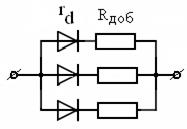
Рисунок 3.7 – Выравнивание токов вентилей

Это невыгодно энергетически, хотя потери в диодах уменьшаются, но результирующие потери из-за R_доб возрастают. Поэтому, в некоторых случаях делают многообмоточный трансформатор (секционированный выпрямитель), как показано на рис. 3.8.

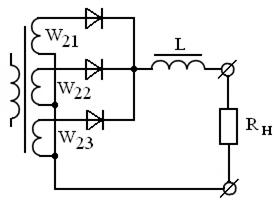
Рисунок 3.8 – Секционированный выпрямитель

Здесь все вторичные обмотки одинаковые. Роль выравнивающих резисторов играют омические сопротивления обмоток. Можно использовать многообмоточный дроссель, как показано на рис.3.9.

Можно применять и то и другое. В цепях питания низковольтных нагрузок используют интегральные диоды – включенные параллельно несколько десятков р–n переходов (20…100 штук), при этом выравнивающих резисторов не требуется, так как все переходы одинаковы, загружены током равномерно и коэффициент загрузки по току не превышает 10…20%, что приводит к снижению результирующих потерь.

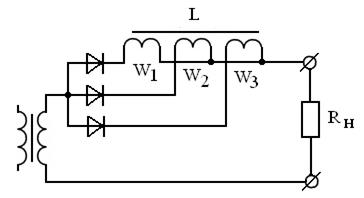
Рисунок 3.9 – Многообмоточный дроссель

Электрическая прочность в обратном направлении – U_{обр доп.}. Особенно важно в высоковольтных выпрямителях. При современных требованиях к частоте переключения время восстановления обратного сопротивления должно быть приблизительно t_восст = 50…100 нс. Здесь подходят диоды Шоттки. Но при обратных напряжениях более 200…300В выбор диодов резко ограничивается. Диоды приходится включать последовательно и выравнивать обратные напряжения внешним делителем, как показано на рис.3.10.

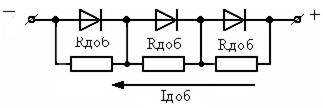
Рисунок 3.10 – Выравнивание обратных напряжений внешним делителем

Ток делителя должен быть больше обратного тока диодов I_доб > I_{обр диода} , иначе не будет выравнивания напряжений. Это существенно увеличивает потери и уменьшает КПД. Можно использовать секционированные выпрямители и складывать напряжения на нагрузке, как показано на рис.3.11.

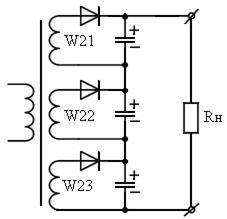
Рисунок 3.11 – Секционированный выпрямитель с суммированием

напряжения

Ударный ток. Для практического использования вентиля в выпрямителе, работающим на ёмкость, представляет интерес допустимая амплитуда серии из 2…4 импульсов тока, следующих с частотой питающей сети (рис.3.12 а). Эта амплитуда называется ударным током (I_пр.уд ), характеризует стойкость диода к перегрузкам и может в 20…50 превышать максимальный ток диода, указанный в справочнике при работе на активную нагрузку.

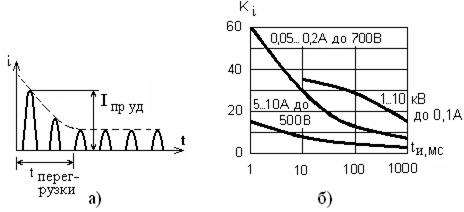
Рисунок 3.12 – Перегрузочная способность диодов

Отношение I_пр.уд / I_пр.ср. называют коэффициентом перегрузки по току К_i. Примерные значения К_i для наиболее распространённых диодов, приведены на рис.3,12 б. Например, диод типа КД219А имеет I_пр.ср. = 10 А, I_пр.уд. = 250 А , при t_и = 10 мс, U_обр. = 15 В, f = 200 кГц.

Быстродействие.В источниках питания с высокочастотным преобразованием энергии используются импульсные или высокочастотные силовые диоды. На эти диоды в справочниках приводится не граничная частота, а время восстановления обратного сопротивления диода. На рис.3.13 показана форма тока диода при переключении.

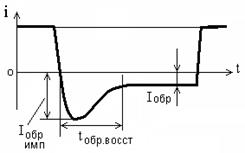
Рисунок 3.13 – Переключение выпрямительного диода

Под граничной частотой (fгр) понимается максимальная частота гармонического сигнала, выше которой заметно возрастают потери мощности за счёт увеличения среднего значения обратного тока. Диод перестает выполнять свои функции, когда t_{обр восст} =Т/2, поэтому

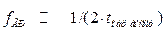(3.2)

Если принять порядок малости равный 10, то для диода КД213А с параметрами I_пр.ср. = 10 А, U_обр. = 200 В, f _ГР = 100 кГц и временем восстановления t _{обр восст} = 0,3мкс получаем граничную частоту, близкую к справочной.

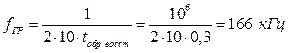(3.3)

Мощность, рассеиваемая в диодескладывается из трёх составляющих: мощности потерь в прямом направлении, в обратном и на переключение.

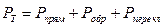, (3.4)

где

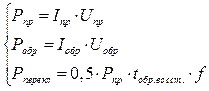(3.5)

Тепло, выделяемое в кремниевой пластине диода (или другого п.п. прибора) передаётся на корпус и далее в окружающую среду через радиатор. Упрощенная тепловая модель полупроводника показана на рис.3.14.

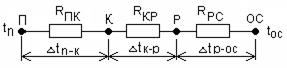
Рисунок 3.14 – Тепловая модель полупроводника

На рисунке обозначено: П – пластина; К – корпус; Р – радиатор; ОС – окружающая среда; t_n –температура пластины; t_ос – температура окружающей среды; R – тепловое сопротивление соответствующего перехода с размерностью [градус/ватт]. Величины тепловых сопротивлений приводятся в справочниках. Они зависят от многих факторов, например, если материал пластины (подложки) ситал, поликор или бериллиевая керамика, то

.

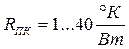Если материал корпуса алюминий, ковар или пластмасса, то

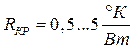
Тепловое сопротивление радиатор – среда зависит от цвета радиатора, конструкции, поверхности, скорости обдува и др. и лежит в пределах

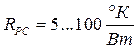
Таким образом, зная температуру окружающей среды, тепловые сопротивления и мощность, рассеиваемую в диоде, находим температуру пластины:

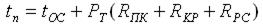
(3.6)

Эта температура не должна превышать максимально допустимую для данного материала (например, для кремния + 140^оС).

Оценка теплового режима с помощью такой модели даёт представление об установившемся тепловом режиме.

Схемы выпрямления

Простейший выпрямитель обычно содержит: трансформатор, вентиль и нагрузку (рис. 3.15).

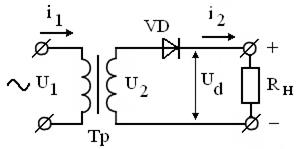
Рисунок 3.15 – Простейший выпрямитель

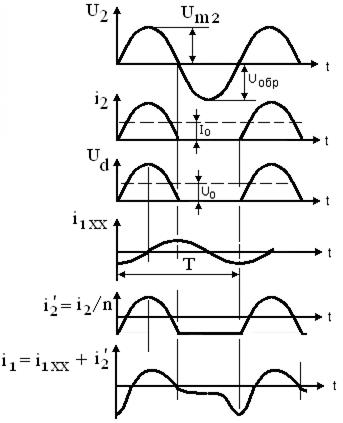
Рисунок 3.16 – Эпюры токов и напряжений простейшего выпрямителя

Это, так называемая, однофазная однотактная схема выпрямления Выпрямленное напряжение (U_d) содержит постоянную составляющую (U₀) и бесконечный ряд гармонических составляющих, первая гармоника которых имеет частоту равную f_сети. За период сети ток i₂ не меняет своего направления, поэтому имеет место постоянное подмагничивание сердечника трансформатора. Ток в первичной обмотке равен сумме тока холостого хода (i_xx) и тока нагрузки, пересчитанного в первичную цепь (i₂^’), который не имеет постоянной составляющей. Форма тока в первичной обмотке (i₁) далека от гармоники, хотя нагрузка активная. В общем случае трансформатор имеет m₁ первичных обмоток (фаз сети) и р фаз во вторичной цепи – число фаз выпрямления, которое называют пульсностью. Обычно m₁ 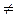p. Пульсность схемы определяется произведением

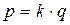, (3.7)

где k – число вторичных обмоток трансформатора

q – число импульсов тока за период в одной обмотке.

Поэтому схема рис. 3.15 называется однофазная и однотактная (р=1*1=1).

Рассмотрим схему с пульсностью р =2, которая приведена на рис.3.17. Здесь две вторичных обмотки и через каждую из них за период сети протекает один импульс тока i₂^’ и i₂^’’. Причём, через нагрузку они протекают в одном направлении, а через вторичные обмотки – в разных направлениях и не создают постоянного подмагничивания сердечника трансформатора. Тогда получаем 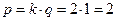, то есть схема двухфазная однотактная.

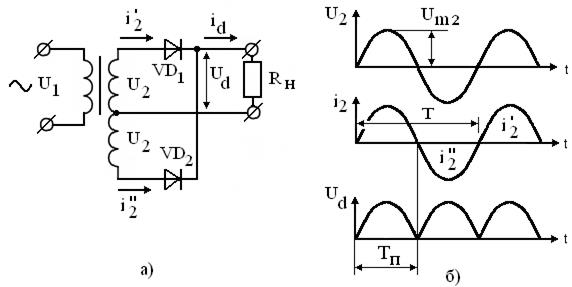
Рисунок 3.17–Двухфазный однотактный выпрямитель (схема со средней точкой)

Частота первой гармоники пульсаций вдвое выше частоты сети (Т_П=Т/2) и находится через пульсность

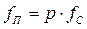(3.8)

Рассмотрим однофазный мост. Его схема приведена на рис.3.18. Эпюры напряжений соответствуют рис.3.17б. Учитывая, что здесь одна вторичная обмотка, находим пульсность 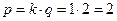, то есть схема однофазная двухтактная. Частота первой гармоники пульсаций вдвое выше частоты сети (как и в предыдущей схеме). Однако они различаются обратными напряжениями на вентилях – в схеме рис. 3.17 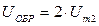, а в схеме 3.18 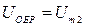. Кроме того, в схеме рис. 3.17 в цепи тока находится только один диод, а в схеме 3.18 – два диода. Поэтому, в низковольтных выпрямителях предпочтительна схема со средней точкой.

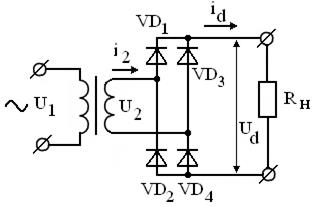
Рисунок 3.18 – Однофазный двухтактный выпрямитель (однофазный

мост)

Рассмотрим трёхфазный выпрямитель.

Трёхфазная однотактная схема выпрямления приведена на рис. 3.19. Эту схему называют также трёхфазной с нулевым выводом или трёхфазной со средней точкой.

Она состоит из трёхфазного трансформатора и трёх вентилей VD1, VD2 и VD3. Нагрузка включается между точкой соединения вентилей и общей точкой вторичных обмоток трансформатора. На рис. 3.20 представлены эпюры токов и напряжений в различных точках схемы.

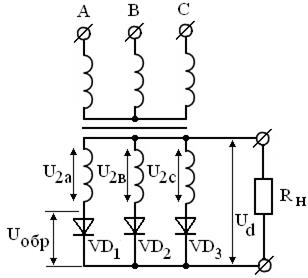
Рисунок 3.19 – Трёхфазная схема с нулевым выводом

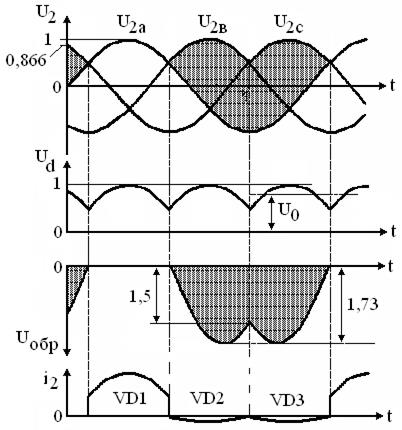
Рисунок 3.20 – Эпюры токов и напряжений для схемы рис.3.19

Трёхфазная двухтактная схема выпрямления (трёхфазный мост или схема Ларионова) приведена на рис. 3.21.

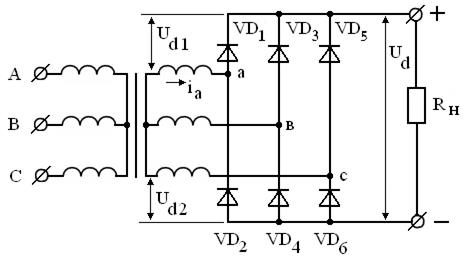
Рисунок 3.21 – Трёхфазная двухтактная схема выпрямления

На рис. 3.22 представлены эпюры токов и напряжений в различных точках схемы. Напряжение на нагрузке является суммой выходных напряжений двух трёхфазных, однотактных выпрямителей, каждый из которых использует свою полуволну фазного напряжения U_d=U_d1+U_d2.

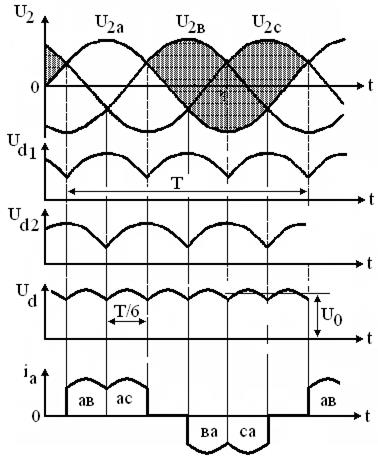
Рисунок 3.22 – Эпюры токов и напряжений для схемы рис.3.21

Учитывая, что здесь три вторичных обмотки, находим пульсность 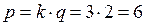. Частота первой гармоники пульсаций .

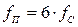Существуют и другие схемы выпрямления с пульсностью 9, 12, 18, 24, 48, 96 и т.д. Это специальные схемы, так называемые, многопульсные выпрямители. Для примера, на рис.3.23 приведена схема 12-пульсного выпрямителя. Она представляет собой последовательное соединение двух трёхфазных мостовых схем. Здесь используется трансформатор с тремя обмотками. Вторичных обмоток две: одна соединяется в звезду, а вторая в треугольник, поэтому вторичные напряжения оказываются сдвинутыми по фазе на угол 30^о. Каждая из вторичных обмоток подключена к мосту, а так как мосты включены последовательно, то сумма напряжений 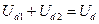содержит 12-кратные пульсации.

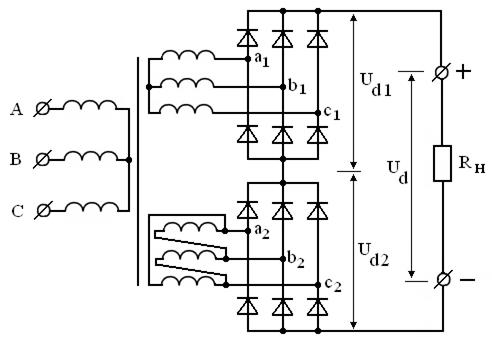
Рисунок 3.23 – 12- пульсная схема выпрямления

Получим количественные соотношения для различных схем выпрямления.

3.4 Расчётные соотношения для неуправляемых выпрямителей

Неуправляемый выпрямитель характеризуется рядом показателей к которым относятся, выходное напряжение – U ₀, коэффициент пульсаций – К_П, частота первой гармоники пульсаций – f_п, коэффициент выпрямления и др. Найдём эти показатели для разных схем выпрямления.

Простейший выпрямитель (рис. 3.15, пульсность р=1). Форма выходного напряжения приведена на рис. 3.24а.

Мгновенное напряжение U_d на интервале 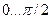подчиняется закону косинуса (повторяет напряжение U₂)

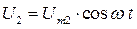(3.9)

Среднее значение выходного напряжения равно

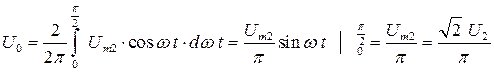. (3.10)

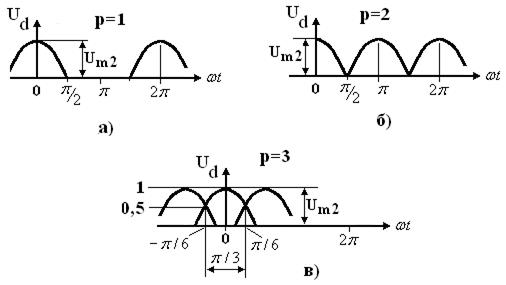
Рисунок 3.24 – Выходное напряжение при разной пульсности

Отношение

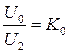(3.11)

называют коэффициентом выпрямления. Он показывает степень использования трансформатора. Для нашего случая

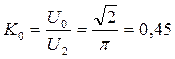(3.12)

т.е. довольно низкая величина.

Найдём теперь коэффициент пульсаций по первой гармонике.

Если грубо принять напряжение U_d гармоническим и считать, что его амплитуда 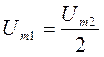, то 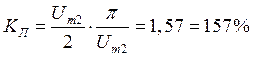. Поэтому, такие схемы без сглаживающих фильтров не используют.

Обратное напряжение на вентиле равно U_обр = U_m2.

Для двухфазной однотактной схемы (рис. 3.17 пульсность р=2).

Среднее значение (постоянная составляющая) выходного напряжения (рис.3.24 б) равно

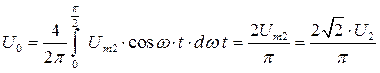(3.13)

Коэффициент выпрямления равен

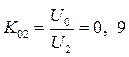(3.14)

Если грубо принять напряжение U_d гармоническим и считать, ч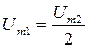то , то 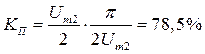. Если же периодическую кривую напряжения Ud разложить в ряд Фурье и выделить первую гармонику, то получим К_П = 0,667. Это соответствует аналитическому выражению

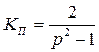, (3.15)

которое справедливо при 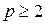. Частота первой гармоники пульсаций кратна частоте сети

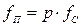
Приведённые соотношения действительны и для мостовой схемы (рис.3.18), поскольку их пульсности одинаковы (р=2). Различными в этих схемах будут обратные напряжения на вентилях, которые соответственно равны:

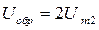для р = 2*1 = 2 (3.16)

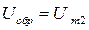для р = 1*2 = 2 (мостовая схема).

Для трёхфазной однотактной схемы (рис. 3.19 пульсность р=3). Форма выходного напряжения приведена на рис. 3.24 в.

Среднее значение выходного напряжения (рис.3.24в) равно

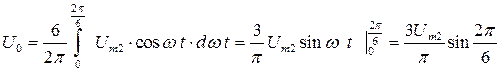(3.17)

Получилась универсальная формула, справедливая при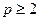

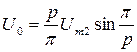(3.18)

Если р =2, то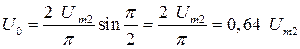

Если р =3, то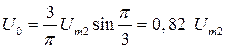

Коэффициент выпрямления равен

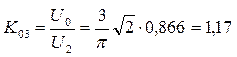(3.19)

Что существенно выше, чем в предыдущих схемах.

Если считать, что пульсации гармонические и их двойная амплитуда

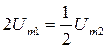, откуда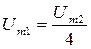

тогда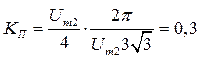

При точном разложении напряжения U_d на гармоники, согласно выражению (3.15) получаем К_П = 0,25.

Обратное напряжение на вентиле равно линейному:

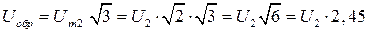(3.20)

Для трёхфазной двухтактной схемы (рис. 3.21 пульсность р=6) получаем:

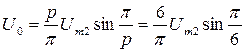(3.21)

В схеме выпрямления вторичные обмотки включены звездой, поэтому U_m2 следует умножить на .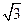

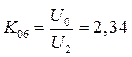(3.22)

К_П = 0,057

При включении вторичных обмоток треугольником множитель 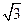не нужен и 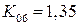. Видно, что с ростом пульсности, растёт коэффициент использования трансформатора и уменьшается коэффициент пульсаций. Поэтому схема Ларионова получила широкое распространение в преобразовательной технике.

В 12- пульсной схеме выпрямления, которая приведена на рис. 3.23 коэффициент пульсаций составляет всего 1,4% и поэтому она может применяться без сглаживающего фильтра.