Анализ и управление производственными запасами
Для финансового менеджера предметно-вещественная природа запасов – сырьё и материалы, незавершённое производство и готовая продукция, а также товары для перепродажи – не имеет особого значения. Важна лишь общая сумма средств, омертвлённых в запасах в течение технологического (производственного) цикла.
Для реализации продукции необходимо определить её себестоимость. Существуют следующие четыре метода, которые могут быть использованы для калькуляции себестоимости реализованной продукции и оценки запасов.
1. Метод индивидуальной оценки [англ. specific identification]. Оценка запасов производится на основе индивидуального учёта затрат по каждой единице продукции. После реализации данной единицы продукции стоимость запасов уменьшается в соответствии с затратами, относящимися к ней.
2. Метод по себестоимости первых по времени закупок [англ. first-in, first-out, FIFO]. Предполагается, что запасы потребляются в той же последовательности, в какой они закупаются фирмой. В результате себестоимость реализованной продукции определяется на основе цен наиболее ранних запасов сырья, а запасы исчисляются в ценах более поздних закупок.
3. Метод по себестоимости последних по времени закупок [англ. last-in, first-out, LIFO]. В этом случае себестоимость реализованной продукции определяется по ценам последних по времени закупок, а оценка запасов производится по ценам ранних закупок.
4. Метод средней себестоимости [англ. average cost]. Определяется средневзвешенная цена единицы запасов, по которой затем производится расчёт себестоимости реализованной продукции.
Поскольку для финансиста запасы – это иммобилизованные ресурсы (хотя без этого отвлечения средств из оборота не обойтись), то вполне естественно желание минимизировать вызываемые этим процессом косвенные потери (равные доходу при инвестировании соответствующей суммы в альтернативный проект). При определённых обстоятельствах эти косвенные потери могут стать прямыми. В случае банкротства предприятия многие оборотные активы попадают в разряд «неликвидов», а вырученная за них сумма – ниже учётной.
Руководство любой компании следует определённым принципам управления запасами, при этом выбирается соответствующий вариант финансирования. Для этого предполагается решение таких задач:
1) какова должна быть структура запасов?
2) каков должен быть объём запасов?
Здесь существует прямо противоположные линии поведения:
· финансирование только за счёт собственных средств;
· исключительно за счёт кредиторов.
Соответственно, выбор той или иной линии поведения может иметь разные последствия с позиции риска, прибыли, текущих расходов, упущенных доходов и т. д.
Алгоритмизация политики управления величиной запасов требует оптимального решения следующих задач:
1) как оптимизировать политику управления величиной запасов?
2) каков должен быть оптимальный объём заказываемой партии?
3) какой объём запасов является минимальным?
4) когда следует заказывать очередную партию запасов?
Что касается величины запасов, то в качестве целевого ориентира следует исходить из затрат, связанных с их поддержанием: затраты по хранению, а также затраты по размещению и выполнению заказов.
С ростом запасов увеличиваются и затраты по хранению. В частности, чем больше завезённая партия запасов, тем в большем объёме требуются складские помещения для их хранения, увеличиваются затраты электроэнергии, увеличивается естественная убыль товаров и т. д. Любой актив не может существовать сам по себе – ему соответствует некоторый источник финансирования, как правило, небесплатный. Поэтому увеличение производственных запасов обычно сопровождается и ростом затрат на поддержание соответствующих источников финансирования.
Затраты по размещению и выполнению заказов имеют обратную зависимость: нет необходимости пользоваться услугами транспортных организаций, более оптимально используется собственный транспорт, есть возможность получить скидку при заказе крупной партии и т. д.
Оба компонента общих затрат, связанных с поддержанием запасов, изменяются обратно пропорционально, поэтому можно найти такую величину среднего запаса, которой соответствует минимальный уровень этих затрат. Представим логику выявления оптимальной партии заказа графически (рис. 6).
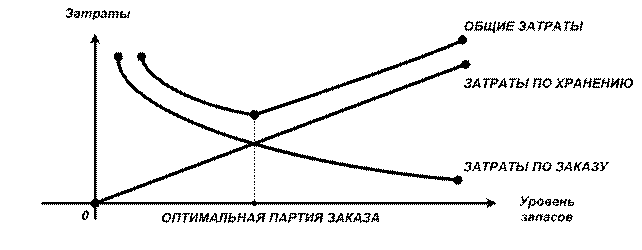
Рис. 6. Определение оптимальной партии заказа
Допустим, что фирма придерживается следующей политики: по мере исчерпания запасов поступает очередная партия сырья и материалов в размере q единиц. В этих условиях средний размер запасов будет равен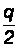 
, а суммарные годовые затраты по поддержанию запасов могут быть найдены по формуле:
,
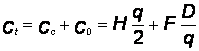где
Сt – общие затраты, р.;
Cc – затраты по хранению, р.;
Cо – затраты по размещению и выполнению заказа р.;
H – затраты по хранению единицы производственных запасов, р.;
q – размер заказываемой партии запасов, ед.;
F – затраты по размещению и выполнению одного заказа (постоянные), р.;
D – годовая потребность в запасах, ед.
Как видно из графика (рис. 6), функция затрат: y = f (q) имеет вид параболы, поэтому, продифференцировав по q, можно найти такое его значение, при котором функция достигает своего минимума. Таким образом, размер оптимальной партии заказа [англ. economic ordering quantity, EOQ] будет иметь вид:
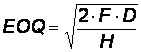
В рамках этой теории разработаны различные схемы управления заказами, позволяющие с помощью ряда параметров формализовать процедуру обновления запасов, в частности определять уровень запасов, при котором необходимо делать очередной заказ.
Варьирование величиной запасов графически выглядит следующим образом (рис. 7).
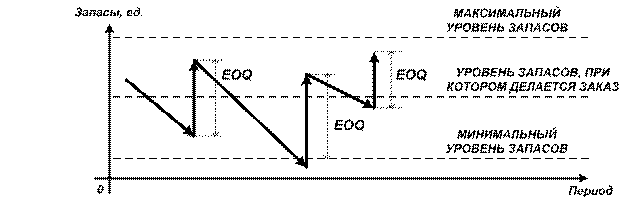
Рис. 7. Динамика финансовых решений в условиях оптимального управления запасами
На основе статистики и экспертных оценок рассчитываются значения исходных факторов. Как только уровень запасов опускается до величины уровня, при котором делается заказ, или ниже, то производится очередной заказ на поставку сырья и материалов. Если поставка осуществляется максимально эффективно, то уровень запасов фирмы может достичь величины максимальной. Если ежедневное потребление сырья и материалов достигло максимума, и по каким-либо причинам поставка очередной партии затянулась, то компании придётся воспользоваться страховым запасом. В этом случае уровень запасов может опуститься ниже величины минимального уровня, а при самых неблагоприятных условиях он может быть равен нулю.
Следовательно, если объём реализации, а также время производства и доставка новой партии запасов подвержены изменениям, которые трудно учесть, то минимальный размер уровня запасов (рис. 7) – это страховой запас, хранящийся на складе, на случай непредвиденной задержки.
Следовательно, применение модели EOQ возможно лишь при условии разделения операционных затрат отдела снабжения на переменные (зависящие от количества заказов и включаемые в расчёты) и постоянные (не зависящие от количества заказов и не включаемые в расчёты).
Поэтому существует ещё одна прикладная модель, используемая для определения оптимального размера запасов готовой продукции [англ. economic production run, EPR]. Эта модификация модели EOQ используется для расчёта оптимального размера партии выпускаемой продукции на основе следующих исходных параметров:
– планового выпуска данного вида продукции;
– затрат производства (оплата труда, амортизация оборудования и пр.) на единицу выпуска готовой продукции;
– издержек по хранению единицы запасов готовой продукции.
Оптимальный размер партии выпуска готовой продукции определяется по формуле:
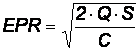
где
Q – плановый выпуск данного вида продукции;
S – затраты производства на единицу данного вида продукции;
C – стоимость хранения единицы запасов готовой продукции.
Дата добавления: 2017-08-01; просмотров: 668;