Анализ поляризованного света

Пусть на кристаллическую пластинку, вырезанную параллельно оптической оси, нормально падает плоскополяризованный свет (рис. 283). Внутри пластинки он разбивается на обыкновенный (о) и необыкновенный (е) лучи, которые в кристалле пространственно не разделены (но движутся с разными скоростями), а на выходе из кристалла складываются.

Так как в обыкновенном и необыкновенном лучах колебания светового вектора совершаются во взаимно перпендикулярных направлениях, то на выходе из пластинки в результате сложения этих колебаний возникают световые волны, вектор Е (а следовательно, и Н) в которых меняется со временем так, что его конец описывает эллипс, ориентированный произвольно относительно координатных осей. Уравнение этого эллипса (см. (145.2)):

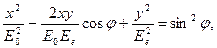(194.1)

где Е₀ и Е_е — соответственно составляющие напряженности электрического поля волны в обыкновенном и необыкновенном лучах, φ — разность фаз колебаний. Таким образом, в результате прохождения через кристаллическую пластинку плоскополяриэованний свет превращается в эллиптически поляризованный.

Между обыкновенным и необыкновенным лучами в пластинке возникает оптическая разность хода

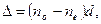
или разность фаз

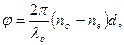
где d — толщина пластинки, λ_о — длина волны света в вакууме.

Если 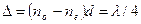, , 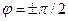то уравнение (194.1) примет вид

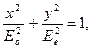
т. е. эллипс ориентирован относительно главных осей кристалла. При Е_о=Е, (если световой вектор в падающем на пластинку плоскополяризованном свете составляет угол α=45° с направлением оптической оси пластинки)

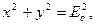
т. е. на выходе из пластинки свет оказывается циркулярно поляризованным.

Вырезанная параллельно оптической оси пластинка, для которой оптическая разность хода

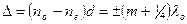
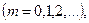
называется пластинкой в четверть волны (пластинкой λ/4). Знак плюс соответствует отрицательным кристаллам, минус — положительным. Плоскополяризованный свет, пройдя пластинку λ/4, на выходе превращается в эллиптически поляризованный (в частном случае циркулярно поляризованный). Конечный результат, как уже рассматривали, определяется разностью фаз φ и углом α.

Пластинка для которой

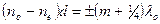
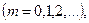
называется пластикой в полволны и т. д.

В циркулярно поляризованном свете разность фаз φ между любыми двумя взаимно перпендикулярными колебаниями равна ±π/2. Если на пути такого света поставить пластинку λ/4, то она внесет дополнительную разность фаз ±π/2. Результирующая разность фаз станет равной 0 или π. Следовательно (см. (194.1)), циркулярно поляризованный свет, пройдя пластинку λ/4, становится плоскополяризованным. Если теперь на пути луча поставить поляризатор, то можно добиться полного его гашения. Если же падающий свет естественный, то он при прохождении пластинки λ/4 таковым и останется (ни при каком положении пластинки и поляризатора погашения луча не достичь).

Таким образом, если при вращении поляризатора при любом положении пластинки интенсивность не меняется, то падающий свет естественный. Если интенсивность меняется и можно достичь полного гашения луча, то падающий свет циркулярно поляризованный; если полного гашения не достичь, то падающий свет представляет смесь естественного и циркулярно поляризованного.

Если на пути эллиптически поляризованного света поместить пластинку λ/4, оптическая ось которой ориентирована параллельно одной из осей эллипса, то она внесет дополнительную разность фаз ±π/2. Результирующая разность фаз станет равной нулю или π. Следовательно, эллиптически поляризованный свет, пройдя пластинку λ/4, повернутую определенным образом, превращается в плоскополяризованный и может быть погашен поворотом поляризатора. Этим методом можно отличить эллиптически поляризованный свет от частично поляризованного или циркулярно поляризованный свет от естественного.