Кинематические следствия из преобразований Лоренца

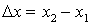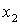Рассмотрим линейку, неподвижную в I, размещенную параллельно оси абсцисс. Длина линейки , где и 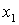- координаты концов линейки в этой системе I.

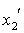В системе II длина этой линейки , где и 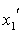следует брать в один и тот же момент .

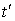Согласно преобразованию Лоренца

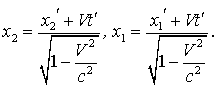
Вычитая, находим

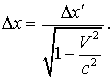
Длина предмета в системе отсчета, в которой он покоится, называется собственной длиной (здесь - 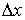). Она наибольшая. В системе, относительно которой линейка движется, она короче 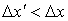, и тем короче, чем больше ее скорость V. Следовательно, длина не является понятием абсолютным (безотносительным к системам отсчета), как принимается в ньютоновой механике.

Пусть в неподвижной точке 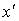системы II произошли два события: первое - в момент 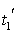, второе - в момент 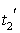. Промежуток времени между этими событиями 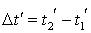. По формулам Лоренца

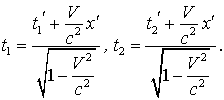
Вычитая значения моментов времени , находим

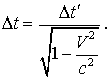(1.8)

Видно, что здесь больше, чем . В системе отсчета, в которой часы покоятся, промежуток времени наименьший. Его называют собственным временем. Иногда этот результат выражают словами: в движущемся теле процессы замедляются.

Примечание 1. В ньютоновой механике сложение скоростей в данной системе отсчета производится по правилу параллелограмма. В СТО это правило также имеет место, если пользоваться только одной отдельно взятой инерциальной системой, а не переходить из одной ИСО в другую, движущуюся.

Примечание 2. При рассмотрении конкретных вопросов полезным бывает следующее представление. В каждой точке пространства имеется двое часов: одни принадлежат системе отсчета I (часы неизменно связаны с системой I), другие " системе II. Движущееся по траектории тело (точка) непрерывно "проходит" по упомянутому множеству часов. Их показания 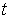и 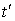(каждый раз в месте нахождения движущегося тела) и есть время, входящее в функции координат 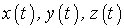и также 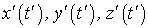. При этом, разумеется, все часы системы I идут синхронно с базовыми часами в начале О этой системы I, а часы системы II - синхронно с базовыми в начале O' системы II движущейся относительно I со скоростью V вместе со всеми своими часами.