Гиперкомплексные системы. Кватернионы.
Программа Maple.
Приложения.
1. Вопросы на доказательства
Лекция № 13
1. Вывод формул коэффициента (Фурье) разложения по ортогональной системе: 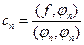 или
или 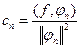 .
.
2. Доказать теорему:Среднеквадратичное отклонение между 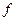 и
и 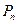 минимально
минимально 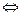 коэффициенты
коэффициенты 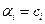 (совпадают с коэффициентами Фурье).
(совпадают с коэффициентами Фурье).
3. Доказать, что если 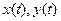 ортогональные функции, то :
ортогональные функции, то :
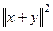 =
= 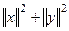 .
.
Лекция № 14
1. Доказать ортогональность основной тригонометрической системы 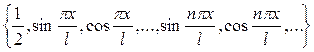
и вычислить квадраты норм функций.
2. Доказать, что ряд Фурье имеет вид 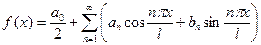 где его коэффициенты:
где его коэффициенты:
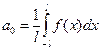 ,
, 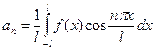 ,
, 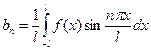 .
.
3. Вывести гармонический вид записи ряда Фурье: 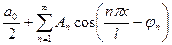
4. Доказать ортогональность системы 
 и вычислить квадраты нормэтих функций.
и вычислить квадраты нормэтих функций.
2. Определения и формулировки.
Лекция № 13
Что такое скалярное произведение функий, норма функции.Приведите пример.
Что такое ортогональные фнукции, ортогональная система функций.
Что такое среднее и среднеквадратичное отклонение.
Напишите вид коэффициента Фцрье по произвольной ортогональной системе.
Лекция № 14
Что такое основная тригонометрическая система?
Что такое периодическое продолжение?
К чему сходится ряд Фурье в точке разрыва?
Какие коэффициенты равны 0 в ряде Фурье в случае чётности либо нечётности функции?
Как вводится скалярное умножение комплекснозначных функций?
Лекция № 15
Что такое интеграл Фурье и преобразование Фурье, запишите формулы.
3. Примеры из лекций.
Лекция № 13
Пример. Разложить функцию 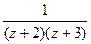 :
:
а) в ряд Лорана в кольце 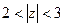
б) во внешней области 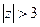
в) в ряд Тейлора в круге 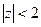 .
.
Пример. Разложить 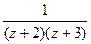 в ряд Лорана по степеням
в ряд Лорана по степеням 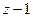 .
.
Пример. Найти скалярное произведение 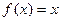 и
и 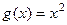 на интервале (0,1).
на интервале (0,1).
Пример. Доказать, что функции 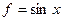 ,
, 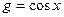 ортогональны на интервале
ортогональны на интервале 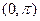 .
.
Лекция № 14
Пример. Разложить в тригонометрический ряд Фурье функцию 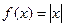 на интервале (-1,1).
на интервале (-1,1).
Пример. Найти комплексный ряд Фурье для функции:
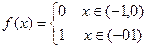
Лекция № 15
Пример. Найти преобразование Фурье для функции 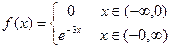
Дата добавления: 2017-06-02; просмотров: 803;
