Передача непрерывных сообщений по каналам связи.
Так же как в случае передачи дискретных сообщений, при наличии шумов непрерывное сообщение 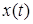 после прохождения канала может быть принято как сообщение
после прохождения канала может быть принято как сообщение 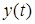 , причем
, причем 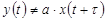 для всех или некоторых моментов времени, где a и τ - константы, характеризующие ослабление и запаздывание сигнала, которые обычно несущественны с точки зрения определения количества информации, содержащегося в сообщении. Такое событие называют ошибкой.
для всех или некоторых моментов времени, где a и τ - константы, характеризующие ослабление и запаздывание сигнала, которые обычно несущественны с точки зрения определения количества информации, содержащегося в сообщении. Такое событие называют ошибкой.
Источник непрерывных сообщений удобно представить в виде непрерывной случайной величины X , которая после прохождения канала преобразуется в непрерывную случайную величину Y . Количество информации в непрерывных случайных величинах Xи Y, при наличии шумов, можно определить предварительно проведя их дискретизацию по уровню (т.е. преобразовав их в дискретные случайные величины), а после определения содержащегося в них количества информации выполнив предельный переход, когда число уровней дискретизации стремится к бесконечности. Эта операция подробно рассмотрена в основах теории информации (§1.8.).
В результате выполнения операций дискретизации по уровню и предельного перехода можно сделать вывод: дифференциальные энтропии случайных непрерывных величин X и Y конечны, хотя их полная энтропия и стремится к бесконечности.
Аналогичным образом можно определить количество информации ( 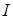 ) случайной величины X , содержащейся в непрерывной случайной величине Y:
) случайной величины X , содержащейся в непрерывной случайной величине Y:
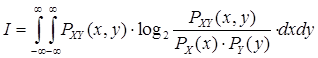 (3.3)
(3.3)
где 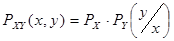 – совместная плотность распределения вероятности величин X и Y;
– совместная плотность распределения вероятности величин X и Y;
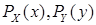 – плотность распределения случайных величин X и Yсоответственно.
– плотность распределения случайных величин X и Yсоответственно.
Из анализа формулы (3.3) можно сделать следующие выводы.
1. Если помехи столь велики, что случайная величина Y практически не зависит от случайной величины X , т.е. 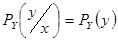 то
то
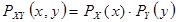
|
и, следовательно, количество получаемой информации ( 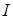 ), вычисленное по формуле (3.3), равно нулю.
), вычисленное по формуле (3.3), равно нулю.
2. Если помеха ( 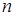 ), представляемая в виде непрерывной случайной величины. носит аддитивный характер, то есть
), представляемая в виде непрерывной случайной величины. носит аддитивный характер, то есть
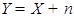 ,
,
причем, случайная величина Xи помеха n независимы (что обычно выполняется), то
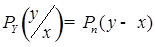 , ,
|
где Pn(y - x) = Pn(n) – плотность распределения вероятности помехи.
В этом случае,
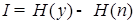 , ,
|
где,
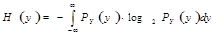 – дифференциальная энтропия сигнала Y; – дифференциальная энтропия сигнала Y;
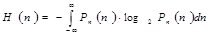 – дифференциальная энтропия шума n. – дифференциальная энтропия шума n.
|
Дата добавления: 2017-05-18; просмотров: 626;
