Упрощение логических выражений.

Прежде чем строить таблицу истинности необходимо определить набор значений для переменных. Для формулы, в которой 2 переменные таких наборов 4: (0,0), (0,1), (1,0), (1,1). Для формулы с тремя переменными: (0,0,0), (0,0,1), (0,1,0), (1,0,0), (0,1,1), (1,0,1), (1,1,0). (1,1,1).
Таблица истинности содержит в себе не только значения переменных, но и значения промежуточных и конечных формул. Рассмотрим примеры.
Пример 1. 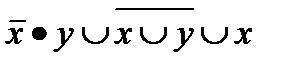
| Переменные | Промежуточные логические формулы | Результат | |||||
| x | y | 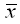
| 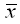 ∙ y ∙ y
| x  y y
| 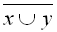
| 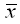 ∙ y ∙ y 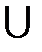 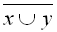
| 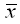 ∙ y ∙ y  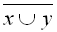  x x
|
Если результат все «1», то эта формула – тождественно истинная. Если результат все «0», то эта формула – тождественно ложная. Если и «0» и «1» - формула выполнимая.

Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Пример.
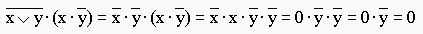
законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами.
Дата добавления: 2017-04-20; просмотров: 1932;
